韶关市2006届高三第一次调研考试
数学试题
第一部分 选择题(共50分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项符合题目要求的.(答案1-10BDAAD CDDDC)
(1)在正项等比数列![]() 中,
中, ![]() 的值为
的值为
A.4 B.8 C.16 D.64
(2)不等式![]() 的解集为
的解集为
A.![]() B.
B.![]()
C.![]() D.
D.![]()
(3)![]() 的值
的值
A.小于零 B.大于零 C.等于零 D.不确定
(4)设定义在R上不恒为0的函数![]() 满足
满足 ![]() ,则
,则![]() 是
是
A.奇函数 B.既是奇函数又是偶函数
C.偶函数 D.既不是奇函数又不是偶函数
(5)若指数函数![]() 的部分对应值如下表:
的部分对应值如下表:
| x | -2 | 0 | 2 |
|
| 0.694 | 1 | 1.44 |
则不等式![]() (x)<0的解集为( )
(x)<0的解集为( )
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
(6)设集合M =![]() ,
,![]() ,若M∩N =
,若M∩N =![]() ,则实数m的取值范围是:( )
,则实数m的取值范围是:( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(7)数列![]() 的前
的前![]() 项和
项和![]()
A.1 B.-1 C. 2 D. -2
(8)已知一次函数![]() 存在反函数,且满足
存在反函数,且满足![]() .则
.则![]()
A.0 B.1 C.2 D.3
(9)已知数列{![]() }中,
}中,![]() =1,前n项和为
=1,前n项和为![]() ,对任意n≥2,总有
,对任意n≥2,总有![]() ,
,![]() ,
,
![]() 成等差数列,则
成等差数列,则![]() ( D )
( D )
A.![]() B.
B. ![]() C. 1
D.
C. 1
D.![]()
(10)设定义域为D的函数![]() 满足以下条件:① 对任意
满足以下条件:① 对任意![]() ;② 对任意
;② 对任意![]() ,当
,当![]() 时,有
时,有![]() .则以下不等式不一定成立的是
.则以下不等式不一定成立的是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
二、填空题
(11)函数![]() 的最小正周期是______________.
的最小正周期是______________.![]()
(12)设函数![]() ,命题P:
,命题P:![]() ;命题Q:方程
;命题Q:方程![]() 有解.则命题Q是命题P的______________ 条件.(必要但不充分)
有解.则命题Q是命题P的______________ 条件.(必要但不充分)
(13)设正方形ABCD的边长为2,点P从点A出发,按A→B→C→D的路径在正方形ABCD的边上移动,以x表示点P走过的路程,![]() 表示三角形APD的面积,当点P在CD边上时,
表示三角形APD的面积,当点P在CD边上时,![]() ____________;其中
____________;其中![]() 的定义域是_______________.
的定义域是_______________.
(14)已知等差数列{![]() }中,
}中,![]() 前n项和为
前n项和为![]() ,且
,且![]() 当
当![]() 最大时,
最大时,![]() ____________;(2005)当
____________;(2005)当![]() 时,
时,![]() 的最大值是____________.(4010)
的最大值是____________.(4010)
三、解答题
(15)求函数![]() 的最大值和最小值.
的最大值和最小值.
解:![]() ………4分
………4分
![]() ………7分
………7分
![]() ……………………………………10分
……………………………………10分
![]() 当
当![]() 时,
时,![]()
当![]() 时,
时,![]() . ……………………………………12分
. ……………………………………12分
(16)已知不等式![]() 的解集是
的解集是![]() ,求不等式
,求不等式![]() 的解集.
的解集.
解:不等式![]() 的解是
的解是 ![]() ,依题设得
,依题设得
![]() 解这个方程组得
解这个方程组得 ![]()
可知不等式![]() 为
为 ![]() 即
即 ![]()
解得 ![]() ,故不等式
,故不等式![]() 的解集是
的解集是![]() .
.
(17)已知公比为![]() 的等比数列
的等比数列![]() 与数列
与数列![]() 满足
满足![]()
(1)
判断![]() 是何种数列,并给出证明;
是何种数列,并给出证明;
(2)
若![]()
解(1)![]()
所以![]() 是以
是以![]() 为公差的等差数列. ……………………………………6分
为公差的等差数列. ……………………………………6分
(2)![]() 所以由等差数列性质得
所以由等差数列性质得![]()
![]()
故 ![]() ……………………………………14分
……………………………………14分
(18)某厂生产某种产品的固定成本为2500元,已知每生产x件这样的产品需要再增大可变成本![]() (元),若生产出的产品都能以每件500元售出,要使利润最大,该厂应生产多少件这种产品?最大利润是多少?
(元),若生产出的产品都能以每件500元售出,要使利润最大,该厂应生产多少件这种产品?最大利润是多少?
解:设该厂生产![]() 件厂品的利润为
件厂品的利润为![]() 元,则:
元,则:
![]() ……………………………………7分
……………………………………7分
![]()
![]()
![]() ……………………………………9分
……………………………………9分
所以当![]() 时,
时,![]() 取得最大值,
取得最大值,![]() …………11分
…………11分
答:要使利润最大,该厂应生产50件这种产品,最大利润为5000元……12分
(19)过定点M(1,0)作曲线![]() 的切线切点为Q1,设Q1点在x轴上的投影是点R1,又过点P1作曲线c的切线切点为Q2,设Q2在x轴上的投影是R2…,依此下去,得到一系列点Q1,Q2,…,Qn,…,设点Qn的横坐标为
的切线切点为Q1,设Q1点在x轴上的投影是点R1,又过点P1作曲线c的切线切点为Q2,设Q2在x轴上的投影是R2…,依此下去,得到一系列点Q1,Q2,…,Qn,…,设点Qn的横坐标为![]()
(1)求证:数列![]() 是等比数列;
是等比数列;
(2)设![]()
![]() ,试比较
,试比较![]() 与
与![]() 的大小(写出推导过程)
的大小(写出推导过程)
(3) 求证: ![]() ;
;
证明(1)![]() ,若切点是Qn(an,anp),则切线方程是
,若切点是Qn(an,anp),则切线方程是![]()
当n=1时,切线过点P(1,0)
即![]() ,得
,得![]() ;………………………2分
;………………………2分
当n>1时,切线过点![]()
即![]()
得![]() ………………………………………………………4分
………………………………………………………4分
所以数列![]()
![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,
的等比数列,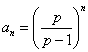 ,
,![]()
…………………………………………………………………………5分
(2)∵![]()
则![]() 两式相减,………………7分
两式相减,………………7分
得
![]() ,…………8分
,…………8分
 ………………………………(10分)
………………………………(10分)
(3)![]()
![]() ……………12分
……………12分
![]() ………………………………(14分)
………………………………(14分)
法二.用数学归纳法证明酌情处理
(20)已知函数![]() 存在极值.
存在极值.
(Ⅰ)如果函数![]() 在区间
在区间![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)设函数![]() 的极小值为
的极小值为![]() ,证明:
,证明:![]() .
.
解:(Ⅰ)![]()
![]()
当![]() 时,
时,![]() ,函数
,函数![]() 在定义域区间
在定义域区间![]() 和
和![]() 上分别为增函数,不存在极值(或:当
上分别为增函数,不存在极值(或:当![]() 时,
时,![]() ,函数
,函数![]() 不存在极值),与题设不符;故
不存在极值),与题设不符;故 ![]() .
.
法1:当![]() 时,
时,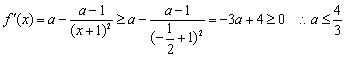
法2:令![]() 解得
解得![]() 或
或![]()
故当![]() 时,函数
时,函数![]() 的增区间为
的增区间为![]()
要函数![]() 在区间
在区间![]() 上单调递增,有
上单调递增,有![]() ,解这个不等式得
,解这个不等式得![]() ,
,![]()
(Ⅱ)由(Ⅰ)知,![]() . 当
. 当![]() 时,
时,
![]() ,函数
,函数![]() 的减区间为
的减区间为![]() ,
,
故函数![]() 只在区间
只在区间![]() 上有一个极小值.
上有一个极小值.
当![]() 时,
时,![]()
![]() (或
(或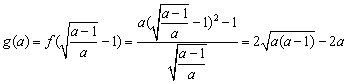 )
)
法1:![]()
又 ![]() ,
,![]()
![]()
法2:![]()
另一方面,![]()
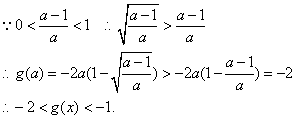
法3:令![]() ,则
,则
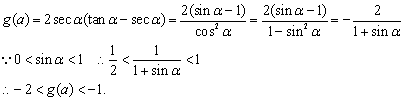
法4:分析法(略)