四川省重点中学高2006级数学能力题训练四
(由四川教科院组织名校教师联合编写)
1.
直线![]() 与椭圆
与椭圆![]() 相交于A、B两点,该椭圆上点P,使得△APB的面积等于3,这样的点P共有
( )
相交于A、B两点,该椭圆上点P,使得△APB的面积等于3,这样的点P共有
( )
A.1个 B.2个 C.3个 D.4个
2.
已知曲线![]() 与其关于点(1,1)对称的曲线有两个不同的交点A和B,如果过这两个交点的直线的倾斜角是
与其关于点(1,1)对称的曲线有两个不同的交点A和B,如果过这两个交点的直线的倾斜角是![]() ,则实数a的值是
( )
,则实数a的值是
( )
A.1 B.![]() C.2 D.3
C.2 D.3
3.
方程![]() 所表示的曲线是
( )
所表示的曲线是
( )
A. 双曲线 B. 抛物线 C. 椭圆 D.不能确定
4.
从-3,-2,-1,1,2,3中任取三个不同的数作为椭圆方程![]() 中的系数,则确定不同椭圆的个数为
( )
中的系数,则确定不同椭圆的个数为
( )
A.20 B.18 C.9 D. 16
5.
如果平面的一条斜线和它在这个平面上的射影的方向向量分别是![]() =(1,0,1),
=(1,0,1),
![]() =(0,1,1),那么这条斜线与平面所成的角是 ( )
=(0,1,1),那么这条斜线与平面所成的角是 ( )
A.90° B.60° C.45° D.30°
6.
四面体的棱长中,有两条为![]() ,其余全为1时,它的体积 ( )
,其余全为1时,它的体积 ( )
A.![]() B.
B.![]() C.
C.![]() D.以上全不正确
D.以上全不正确
7. 已知铜的单晶体的外形是简单几何体,单晶铜有三角形和八边形两种晶面,如果铜的单晶体有24个顶点,每个顶点处有3条棱,那么单晶铜的三角形晶面和八边形晶面的数目分别是 ( )
A.6,8 B.8,6 C.8,10 D.10,8
8.
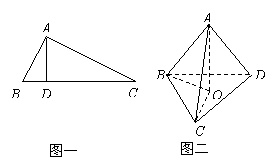 如图一,在△ABC中,AB⊥AC、AD⊥BC,D是垂足,则
如图一,在△ABC中,AB⊥AC、AD⊥BC,D是垂足,则![]() (射影定理)。类似有命题:三棱锥A-BCD (图二)中,AD⊥平面ABC,AO⊥平面BCD,O为垂足,且O在△BCD内,则
(射影定理)。类似有命题:三棱锥A-BCD (图二)中,AD⊥平面ABC,AO⊥平面BCD,O为垂足,且O在△BCD内,则![]() ,
,
上述命题是 ( )
A.真命题
B.假命题
C.增加“AB⊥AC”的条件才是真命题
D.增加“三棱锥A-BCD是正三棱锥”
的条件才是真命题
9. 下列各式中,若1<k<n, 与Cnk不等的一个是 ( )
A.![]() Cn+1k+1 B.
Cn+1k+1 B.![]() Cn-1k-1 C.
Cn-1k-1 C.![]() Cn-1k D.
Cn-1k D.![]() Cn-1k+1
Cn-1k+1
10. 从10名女学生中选2名,40名男生中选3名,担任五种不同的职务,规定女生不担任其中某种职务,不同的分配方案有 ( )
A.P102P403 B.C102P31P44C103 C.C152C403P55 D.C102C403
11.
如果一个三位正整数形如“![]() ”满足
”满足![]() ,则称这样的三位数为凸数(如120、363、374等),那么所有凸数个数为 ( )
,则称这样的三位数为凸数(如120、363、374等),那么所有凸数个数为 ( )
A.240 B.204 C.729 D.920
12.
使得多项式![]() 能被5整除的最小自然数为 ( )
能被5整除的最小自然数为 ( )
A.1 B.2 C.3 D.4
13. 已知两个正数x,y满足x+y=4,则使不等式![]() ≥m,恒成立的实数m的取值范围是
≥m,恒成立的实数m的取值范围是
14. 已知![]() >b,
>b,![]() ·b=1则
·b=1则![]() 的最小值是
的最小值是
15.
已知圆C的方程为![]() 定点M(x0,y0),直线
定点M(x0,y0),直线![]() 有如下两组论断:
有如下两组论断:
第Ⅰ组 第Ⅱ组
(a)
点M在圆C内且M不为圆心 (1) 直线![]() 与圆C相切
与圆C相切
(b) 点M在圆C上
(2) 直线![]() 与圆C相交
与圆C相交
(c )点M在圆C外
(3) 直线![]() 与圆C相离
与圆C相离
由第Ⅰ组论断作为条件,第Ⅱ组论断作为结论,写出所有可能成立的命题 .
(将命题用序号写成形如![]() 的形式)
的形式)
16. 过直线![]() 上一点M向圆
上一点M向圆![]() 作切线,则M到切点的最小距离为
作切线,则M到切点的最小距离为
_ ____.
17.
设曲线![]() 在点
在点![]() 处的切线斜率为
处的切线斜率为![]() ,且
,且![]() ,对一切实数
,对一切实数![]() ,不等式
,不等式![]() 恒成立(
恒成立(![]() ).
).
(1)求![]() 的值;
的值;
(2)求函数![]() 的表达式;
的表达式;
(3)求证:![]() .
.
18.
m解关于![]() 的不等式
的不等式![]() >0.
>0.
19. 如图9-3,已知:射线OA为y=kx(k>0,x>0),射线OB为y= -kx(x>0),动点P(x,y)在∠AOx的内部,PM⊥OA于M,PN⊥OB于N,四边形ONPM的面积恰为k.
(1)当k为定值时,动点P的纵坐标y是横坐标x的函数,求这个函数y=f(x)的解析式;
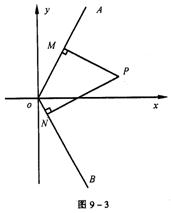 (2)根据k的取值范围,确定y=f(x)的定义域.
(2)根据k的取值范围,确定y=f(x)的定义域.
20.
已知A、B、C是长轴长为4的椭圆上的三点,点A是长轴的一个顶点,BC过椭圆中心O,如图,且![]() ·
·![]() =0,BC=2AC,
=0,BC=2AC,
(1)求椭圆的方程;
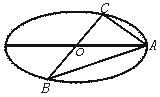 (2)如果椭圆上两点P、Q使∠PCQ的平分线垂直AO,则是否存在实数λ,使
(2)如果椭圆上两点P、Q使∠PCQ的平分线垂直AO,则是否存在实数λ,使![]() =λ
=λ![]() ?
?
请说明理由..
21. 已知一条曲线上的每个点到A(0,2)的距离减去它到x轴的距离差都是2.
(1)求曲线的方程;
(2)讨论直线A(x-4)+B(y-2)=0(A,B∈R)与曲线的交点个数.
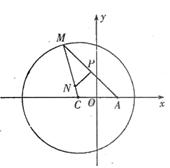
22.如图所示,已知圆![]() 为圆上一动点,点P在AM上,点N在CM上,且满足
为圆上一动点,点P在AM上,点N在CM上,且满足![]() 轨迹为曲线E.
轨迹为曲线E.
(1)求曲线E的方程;
|
高三数学能力训练4参考答案
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| B | C | A | B | B | A | B | A | D | B | A | C |
13. m≤9/4
14. ![]()
15. ![]() 9
9
16. ![]()
17. ⑴解:![]() ,
,
![]() ,
, ![]() ,
, ![]() ……4分
……4分
![]()
![]()
![]()
![]() (2)解:
(2)解:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]() ,
,
又![]() 即
即![]()
![]() …………8分
…………8分
(3)证明:![]() ,
,![]() 原式
原式![]() …
…![]()
![]() …
…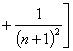
![]() …
…![]()
![]() …
…![]()
18.
解:原不等式可化为![]() >0。 即
>0。 即![]() >0
>0![]() x(
x(![]() -1)>0……3分
-1)>0……3分
当m>0 时,解得x<0或x>![]() ……6分
……6分
当m<0时,解得![]() <x<0
……9分
<x<0
……9分
当m=0时,解得x<0 ……11分
综上,当m>0时,不等式的解集为![]() {
{![]() <0或x>
<0或x>![]() }
}
当m<0时,不等式的解集为{![]()
![]() <x<0}
<x<0}
当m=0时, 不等式的解集为{![]() <0.}
……12分
<0.}
……12分
19. (1)设M(a,ka),N(b,-kb),(a>0,b>0)。
则OM=a![]() ,ON=b
,ON=b![]() 。
。
由动点P在∠AOx的内部,得0<y<kx。
∴PM=![]() =
=![]() ,PN =
,PN =![]() =
=![]()
∴S四边形ONPM=S△ONP+S△OPM=![]() (OM·PM+ON·PN)
(OM·PM+ON·PN)
=![]() [a(kx-y)+b(kx+y)]=
[a(kx-y)+b(kx+y)]=![]() [k(a+b)x - (a-b)y]=k
[k(a+b)x - (a-b)y]=k
∴k(a+b)x-(a-b)y=2k ①
又由kPM=
-![]() =
=![]() , kPN=
, kPN=![]() =
=![]() ,
,
分别解得a=![]() ,b=
,b=![]() ,代入①式消a、b,并化简得x2-y2=k2+1。
,代入①式消a、b,并化简得x2-y2=k2+1。
∵y>0,∴y=![]()
(2)由0<y<kx,得 0<![]() <kx
<kx
![]()
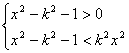
![]()
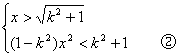 (*)
(*)
当k=1时,不等式②为0<2恒成立,∴(*)![]() x>
x>![]() 。
。
当0<k<1时,由不等式②得x2<![]() ,x<
,x<![]() ,∴(*)
,∴(*)![]()
![]() <x<
<x<![]() 。
。
当k>1时,由不等式②得x2>![]() ,且
,且![]() <0,∴(*)
<0,∴(*)![]() x>
x>![]()
但垂足N必须在射线OB上,否则O、N、P、M四点不能组成四边形,所以还必须满足条件:y<![]() x,将它代入函数解析式,得
x,将它代入函数解析式,得![]() <
<![]() x
x
解得![]() <x<
<x<![]() (k>1),或x∈k(0<k≤1).
(k>1),或x∈k(0<k≤1).
综上:当k=1时,定义域为{xx>![]() };
};
当0<k<1时,定义域为{x![]() <x<
<x<![]() };
};
当k>1时,定义域为{x![]() <x<
<x<![]() }.
}.
20. ⑴以O为原点,OA所在的直线为x轴建立如图所示的直角坐标系
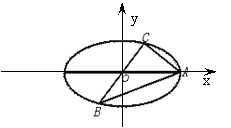 则A(2,0),设所求椭圆的方程为:
则A(2,0),设所求椭圆的方程为:![]() =1(0<b<2),
=1(0<b<2),
由椭圆的对称性知OC=OB,由![]() ·
·![]() =0得AC⊥BC,
=0得AC⊥BC,
∵BC=2AC,∴OC=AC,
∴△AOC是等腰直角三角形,∴C的坐标为(1,1),
∵C点在椭圆上
∴![]() =1,∴b2=
=1,∴b2=![]() ,所求的椭圆方程为
,所求的椭圆方程为![]() =1
……………5分
=1
……………5分
(2)由于∠PCQ的平分线垂直OA(即垂直于x轴),不妨设直线PC的斜率为k,则直线QC的斜率为-k,直线PC的方程为:y=k(x-1)+1,直线QC的方程为y=-k(x-1)+1,
由![]() 得:(1+3k2)x2-6k(k-1)x+3k2-6k-1=0(*) ……………8分
得:(1+3k2)x2-6k(k-1)x+3k2-6k-1=0(*) ……………8分
∵点C(1,1)在椭圆上,∴x=1是方程(*)的一个根,则其另一根为![]() ,设P(xP,yP),Q(xQ,yQ),xP=
,设P(xP,yP),Q(xQ,yQ),xP=![]() , 同理xQ=
, 同理xQ=![]() ,
,
kPQ=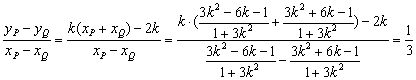 ………10分
………10分
而由对称性知B(-1,-1),又A(2,0) ∴kAB=![]()
∴kPQ=kAB,∴![]() 与
与![]() 共线,且
共线,且![]() ≠0,即存在实数λ,使
≠0,即存在实数λ,使![]() =λ
=λ![]() . ……12分
. ……12分
21.
解:(1)设点M(x,y)是曲线上任意一点,则![]() -y=2,
-y=2,
整理![]() =y+2,
=y+2,
所求曲线的方程. C1:当y³0时, x2=8y;
C2:当y<0时,x=0. ……………5分
(2)直线A(x-4)+B(y-2)=0过定点(4,2)且A、B不同时为零,
(数形结合)当B=0时,A¹0,直线x=4与曲线有1个的交点; ……………7分
当B¹0时,令k=-![]() ,则y=k(x-4)+2,与x2=8y联列:x2-8kx+32k-16=0
,则y=k(x-4)+2,与x2=8y联列:x2-8kx+32k-16=0
当D=0时,k=1,即A=-B时,直线与C1和C2各一个交点;
当k>1时,![]() <-1时,直线与C1两个交点,和C2一个交点;
<-1时,直线与C1两个交点,和C2一个交点;
当![]() <k<1时,-1<
<k<1时,-1<![]() <-
<-![]() 时,直线与C1两个交点,和C2一个交点;
时,直线与C1两个交点,和C2一个交点;
当k£![]() 时,
时,![]() ³-
³-![]() 时,直线与C1和C2各一个交点.
……………10分
时,直线与C1和C2各一个交点.
……………10分
![]() 直线与曲线有1个的交点,当B=0时,A¹0;
直线与曲线有1个的交点,当B=0时,A¹0;
直线与曲线有2个的交点, A=-B和![]() ³-
³-![]() ;
;
直线与曲线有3个的交点, -1<![]() <-
<-![]() 和
和![]() <-1.
……………12分
<-1.
……………12分
22. 解:(1)![]()
∴NP为AM的垂直平分线,∴NA=NM.…………………………2分
又![]()
∴动点N的轨迹是以点C(-1,0),A(1,0)为焦点的椭圆.
且椭圆长轴长为![]() 焦距2c=2.
焦距2c=2. ![]() ……………5分
……………5分
∴曲线E的方程为![]() ………………6分
………………6分
(2)当直线GH斜率存在时,
设直线GH方程为![]()
得![]()
设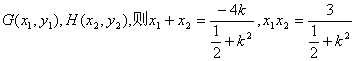 ……………………8分
……………………8分
![]()
![]() ,
,
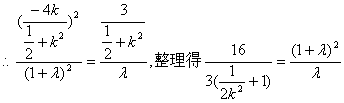 ……………………10分
……………………10分
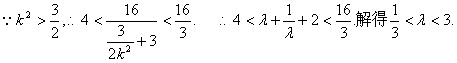
![]()
又当直线GH斜率不存在,方程为![]()
![]() ……………………………………12分
……………………………………12分