四川省重点中学高2006级数学能力题训练五
（由四川教科院组织名校教师联合编写）
1. 用1，2，3，4，5，6，7七个数字排列组成七位数，使其中偶位数上必定是偶数，那么可得七位数的个数是 （ ）
A．P44 B．P44P33 C．6P33 D．C152C403P55
2. 设(1－2x)10＝a1+a2x+a3x2+…+a11x10， 则a3+a5+…+a7+a9等于 （ ）
A．310－1 B．1－310 C．
(310－1) D．(310+1)
3. 某校高三年级举行一次演讲赛共有10位同学参赛，其中一班有3位，二班有2位，其它班有5位，若采用抽签的方式确定他们的演讲顺序，则一班有3位同学恰好被排在一起（指演讲序号相连），而二班的2位同学没有被排在一起的概率为 （ ）
A．
B．
C．
D．
4. 一台X型号自动机床在一小时内不需要工人照看的概率为0.8000,有四台这中型号的自动机床各自独立工作,则在一小时内至多2台机床需要工人照看的概率是 （ ）
A．0.1536 B．0.1808 C．0.5632 D．0.9728
5. 甲、乙两人独立地解同一问题，甲解决这个问题的概率是p1，乙解决这个问题的概率是p2，那么恰好有1人解决这个问题的概率是 （ ）
A．
B．
C．
D．
6. 编号1，2，3，4，5，6的六个球分别放入编号为1，2，3，4，5，6的六个盒子中，其中有且只有三个球的编号与盒子的编号一致的放法种数有 （ ）
A．20 B．40 C．120 D．480
7. 同一天内，甲地下雨的概率是0.15，乙地下雨的概率是0.12，假定在这天两地是否下雨相互之间没有影响，那么甲、乙两地都不下雨的概率是 （ ）
A．0.102 B．0.132 C．0.748 D．0.982
8. A，B，C，D，E五种不同的商品要在货架上排成一排，其中A，B两种商品必须排在一起，而C，D两种商品不能排在一起，则不同的排法共有 （ ）
A．12种 B．20种 C．24种 D．48种
9. 从2004名学生中选取50名组成参观团,若采用下面的方法选取: 先用简单随机抽样从2004人中剔除4人,剩下的2000人再按系统抽样的方法进行.则每人入选的概率（ ）
A．不全相等 B．均不相等
C．都相等,且为
D．都相等,且为
10.
一点沿直线运动,如果由始点起经过t秒后的距离为s=
t4－
t3+2t2，那么速度为零的时刻是 （ ）
A．1秒末 B．0秒 C．4秒末 D．0,1,4秒末
11.
设直线 ax+by+c=0的倾斜角为
，且sin+cos=0，则a,b满足
（ ）
A．
B．
C．
D．
12. 把正方形ABCD沿对角线AC折起，当A、B C、D四点为顶点的三棱锥体积最大时，直线BD与平面ABC所成的角的大小为 （ ）
A．90° B．60° C．45° D．30°
13. 若椭圆
=1的离心率为
，则k的值为 .
14. 一个正方体的棱长为2，将八个直径各为1的球放进去之后，正中央空间能放下的最大的球的直径为__________________.
15. 某学校要从高三的6个班中派9名同学参加市中学生外语口语演讲，每班至少派1人，则这9个名额的分配方案共有 种.（用数字作答）
16. 在
的展开式中，
项的系数是
17.
已知定点
，动点
（异于原点）在
轴上运动，连接PF，过点作
交
轴于点
，并延长
到点
，且
，
.
（1）求动点的轨迹
的方程；
（2）若直线
与动点的轨迹交于
、
两点，若
且
，求直线的斜率
的取值范围．
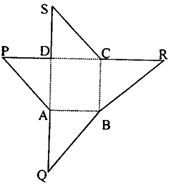
18. 如图为某一几何体的展开图，其中ABCD是边长为6的正方形，SD=PD=6，CR=SC，AQ=AP，点S、D、A、Q及P、D、C、R共线.
（1）沿图中虚线将它们折叠起业，使P、Q、R、S四点重合，请画出其直观图，试问需要几个这样的几何体才能拼成一个棱长为6的正方体ABCD—A1B1C1D1？
|
19.
已知在四面体ABCD中，
= a，
= b，
= c，G∈平面ABC．
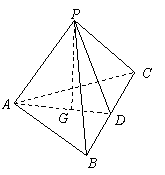（1）若G为△ABC的重心，试证明
(a+b+c)；
（2）试问（1）的逆命题是否成立？并证明你的结论．
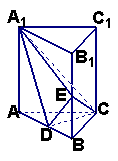
20. 如图，直三棱柱ABC-A
BC中，AC=BC=AA=2， 
，E为BB中
点，
.
（1）求证：CD
面AABB;
（2）求二面角C-AE-D的大小.
21. 如图，四棱锥P—ABCD中，PB⊥底面ABCD，CD⊥PD.底面ABCD为直角梯形，AD∥BC，AB⊥BC，AB=AD=PB=3.点E在棱PA上，且PE=2EA.
|
（2）求证：PC∥平面EBD；
（3）求二面角A—BE—D的大小.（用反三角函数表示）.
22.
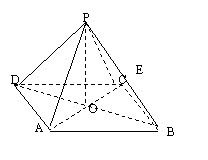
如图所示：正四棱锥
中，侧棱
与底面
所成的角的正切值为
，
（1）求侧面
与底面所成的二面角的大小；
（2）若E是
的中点，求异面直线PD与AE所成角的正切值；
（3）在侧面上寻找一点F，使EF⊥侧面
，试确定点
的位置，并加以证明．
高三数学能力训练5参考答案
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| B | C | D | D | B | B | C | C | C | D | D | C |
13. 4或－5/4 14.
15.56 16.135
17.解 (1)设动点的的坐标为
，则
，
，由得，
，
因此，动点的轨迹的方程为
. …………5分
(2)设直线的方程为
，与抛物线交于点
，则由，得
，又
，故
.
又
，
∴
，
，
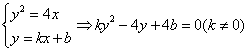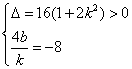∴即
解得直线的斜率的取值范围是
. ……………………12分
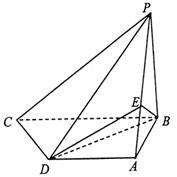
18.（1）它是有一条侧棱垂直于底面的四棱锥（见右图），
需要3个这样的几何体可以拼成一个正方体.……（6分）
（2）解法一：设B1E，BC的延长线交于点G，连结GA，
在底面ABC内作BH⊥AG，垂足为H，连结HB1，由
三垂线定理知，B1H⊥AG，则∠B1HB为平面AB1E与
平面ABC所成二面角的平面角，……（8分）
在Rt△ABG中，AG=
则BH=
B1H=
，……（10分）
，所以平面AB1E与平面ABC所成二面角的余弦值为
12分
解法二：以C为原点，CD、CB、CC1所在直线分别为x、y、z轴，建立直角坐标系，设棱长为6，则E（0，0，3），B1（0，6，6），A（6，6，0）.……8分
设向量n=（x，y，z），满足n⊥
，n⊥
，
于是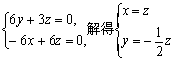
，…………10分
取z=2，得n=（2，－1，2），又
=（0，0，6），则
…12分
19.解：（1）连AG交BC于D，则D平分BC，且G分
所成的比为2∶1，从而
，
，
故
．
（2）逆命题成立，证明如下：
设D分
所成的比为p，G分所成的比为q．
则
， 
，
于是，
=
因(a+b+c)，故
，
解得q =2，p = 1，于是G为△ABC的重心．
21. 21．解法一：
（1）∵PB⊥底面ABCD，CD⊥PD，∴CD⊥BD.
在直角梯形ABCD中，AB=AD=3，∴BC=6. ……………………2分
取BC的中点F，连结PF，则AF//CD.
∴异面直线PA和CD所成的角就是PA和AF所成的角∠PAF.
在△PAF中，
……4分
（2）连结AC交BD于G，连结EG，
（3）∵PB⊥平面ABCD，∴AD⊥PB.
又∵AD⊥AB，∴AD⊥平面EAB.……9分
作AE⊥BE，垂足为H，连结DH，则DH⊥BE，
∴∠AHD是二面角A—BE—D的平面角. ……10分
解法二：（1）建立如图所示的直角坐标系B—xyz.
（1）同解法一.
（2）设平面BED的法向量为
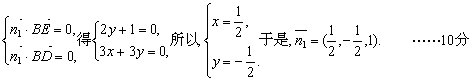
又因为平面ABE的法向量
所以，二面角A—BE—D的大小数点为
……12分
22. 解：(1)取AD中点M，设PO⊥面ABCD，连MO、PM，则∠PMO为二面角的平面角，∠PAO为侧棱PA与底面ABCD所成的角，tan∠PAO=,
设AB=a，AO=
a
PO=AO·tan∠POA=
a
tan∠PMO=
=
∴∠PMO=60°. ……………………………… 4分
(2)连OE，OE∥PD，∠OEA为异面直线PD与AE所成的角，
AO⊥BD AO⊥平面PBD
AO⊥OE
AO⊥PO OE
平面PBD
OE=PD=
=
a
∴tan∠AEO=
=
.
………………8分
3)延长MO交BC于N，取PN中点G，连EG、MG，
BC⊥MN
BC⊥平面PMN
BC⊥PN
平面PMN⊥平面PBC
PM=PN
△PMN为正△MG⊥PN
∠PMN=60°
平面PMN∩平面PBC=PN MG⊥平面PBC
取AM中点F，因为EG∥MF
MF=MA=EG
EF∥MG ∴EF⊥平面PBC. …………………… 14分