如皋市2006～2007学年度第一学期高三期初调研考试
数 学 试 卷
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，第I卷1～2页，第II卷3～8页.全卷满分150分，考试时间120分钟．
第I卷（选择题，共60分）
注意事项：
1．答第I卷前，考生务必在答题卡的相应栏目内写上自己的姓名、准考证号、考试科目，并用铅笔涂写在答题卡上.
2．选择题部分每小题选出答案后，用铅笔把答题卡上对应的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，不能答在试题卷上.
3.考试结束，将答题卡和第II卷一并交回.
一．选择题：本大题共有12小题，每小题5分，共60分．在每小题给出的四个选项中，有且只有一项是符合题目要求的．
1．下列集合中，恰有2个元素的集合是
A．
B．
C．
D．
2．函数
的周期与函数
的周期相等，则
等于
A．2
B. 1
C. 
D. 
3．定义
. 若A={2, 4, 6, 8, 10}，B={1, 4, 8}，则
A．{4，8} B．{1，2，6，10} C．{1} D．{2，6，10}
4．若要得到函数y=sin(2x－
)的图象，可以把函数y=sin2x的图象
A. 向右平移
个单位
B. 向左平移个单位
C. 向右平移个单位
D. 向左平移个单位
5. 原命题“设
R，若
，则
.”的逆命题、否命题、逆否命题中，真命
题共有
A.0个 B.1个 C.2个 D.3个
6．在△ABC中，tanA是以－4为第3项，4为第7项的等差数列的公差；tanB是以
为第
3项，9为第6项的等比数列的公比，则该三角形是
A. 锐角三角形 B. 直角三角形
C. 钝角三角形 D. 等腰三角形
7. 对于函数f(x)=ax2+bx+c（a≠0），若作代换x=g(t)，则不改变函数f(x)的值域的代换是
A．g(t)=
B．g(t)=t C．g(t)=sint D．g(t)=
8．函数
在[0，1]上是减函数，则a的取值范围是
A．（0，1） B．（0，2） C．（1，2） D．
9. 四个实数－9，a1，a2，－1成等差数列，五个实数－9，b1，b2，b3，－1成等比数列，则
b2（a2－a1）等于
A. 8 B.
－8
C. ±8
D.
10.有容积相等的桶A和桶B，开始时桶A中有a升水，桶B中无水. 现把桶A的水注入桶B，
t分钟后，桶A的水剩余
（升），其中m为正常数. 假设5分钟时，桶A和桶B
的水相等，要使桶A的水只有
升，必须再经过
A.7分钟 B.8分钟 C.9分钟 D.10分钟
11.设
是等比数列，有下列四个命题：①
一定是等比数列；②
一定是等
比数列；③
一定是等比数列；④
一定是等比数列. 其中正确命题的个数是
A. 1 B. 2 C. 3 D. 4
12. 已知三个不等式：
（其中a，b，c，d均为实数），用其
中两个不等式作为条件，余下的一个不等式作为结论组成一个命题，可组成的正确命题
的个数是
A. 0 B. 1 C. 2 D. 3
第II卷（非选择题，共90分）
注意事项：
1. 第II卷共6页，用钢笔或圆珠笔直接答在试卷上.
2.答卷前将密封线内的项目填写清楚.
| 题 号 | 二 | 三 | II卷总分 | 合分人 | ||||
| 19 | 20 | 21 | 22 | 23 | ||||
| 得 分 | ||||||||
| 得分 | 评卷人 |
二．填空题：本大题共6小题，每小题4分，共24分．将答案填在题中的横线上．
13. 已知全集
，
，
，则
＝
.（用列举法表示）
14. 设是公差为2 的等差数列，如果
，那么
＝ ．
15. 设
是定义域为R且最小正周期为
的函数，在一个周期内若
=
.
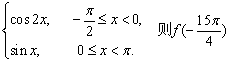16. 已知正数x、y满足x＋2y＝1，则
的最小值是
.
17．规定记号“
”表示两个正数间的一种运算：
．若
，则函数
的值域是 ．
18. 已知点
是函数
图象上的两个不同点，且
，
给出下列不等式：①
；②
；③
；
④
. 其中正确不等式的序号是 .
三．解答题：本大题共5小题，共66分．解答应写出文字说明、证明过程或演算步骤．
| 得分 | 评卷人 |
19．（本小题满分12分）
等差数列中，前（2k＋1）项（
）之和为77，其中偶数项之和为33，且a1－a2k＋1＝18，求数列的通项公式.
| 得分 | 评卷人 |
20．（本小题满分12分）
已知函数
满足
(1)求函数解析式及定义域;
(2)求函数的反函数
;
(3)若
，求x的取值范围.
| 得分 | 评卷人 |
21. （本小题满分14分）
若定义在R上的函数f(x)为奇函数，且在
上是增函数.
(1)求证：f(x)在
上也是增函数；
(2)对任意
，不等式
恒成立,求实数m的取值范围.
| 得分 | 评卷人 |
22. （本小题满分14分）
已知A、B、C为△ABC的三个内角，设
.
（1）当f (A, B)取得最小值时，求C的大小；
（2）当
时，记h（A）＝f (A, B)，试求h（A）的表达式及定义域；
（3）在（2）的条件下，是否存在向量p，使得函数h（A）的图象按向量p平移后得
到函数
的图象？若存在，求出向量p的坐标；若不存在，请说明
理由.
| 得分 | 评卷人 |
23. （本小题满分14分）
设Sn是数列的前n项和，且
．
（1）求数列的通项公式；
（2）设数列
使
，求的通项公式；
（3）设
，且数列
的前n项和为Tn，试比较Tn与
的大小．
高三数学参考答案及评分标准
说明：
1.本解答仅给出了一种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容对照评分标准制订相应的评分细则．
2. 评阅试卷，应坚持每题评阅到底，不要因为考生的解答中出现错误而中断对该题的评阅，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应得分数的一半；如果后继部分的解答有较严重的错误，就不再给分．
3. 解答右端所注分数，表示考生正确做出这一步应得的分数．
4. 给分或扣分均以1分为单位．选择题和填空题不给中间分．
一．选择题：每小题5分，共60分．
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | C | D | A | B | A | D | C | B | D | B | C |
二、填空题：每小题4分，共24分
13．
14．74
15．
16．
17．
18．②③
三、解答题：
19．（12分）前（2k＋1）项中偶数项共有k项. …………1分
设等差数列的公差为d，由题意得
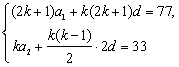即
…………3分
∵
， ∴
解得k＝3.
…………2分
∵a1－a2k＋1＝
，∴＝18，∴d＝－3.
…………2分
将k＝3，d＝－3代入①得a1＝20. …………2分
故
…………2分
20．（12分）（1）设t＝x－3，则x＝t＋3.
∵ 
∴
…………1分
∵ 
，∴
由
得
…………2分
于是
且定义域为[0，2].
…………1分
（2）设y＝ 则
，即
，
∴
.
…………2分
∵
∴
，∴ 
从而
.
故函数的反函数为（
）.
…………2分
（3）
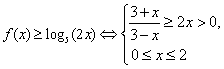
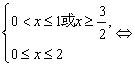
…………4分
21．（14分） （1）设x1<x2
0, 则－x1>－x2
0.
∵f (x)在上是增函数，∴f (－x1) > f (－x2).
…………2分
∵f(x)为奇函数，∴f (－x1)＝－f (x1)，f (－x2)＝－f (x2). …………2分
于是－f (x1) > －f (x2)，即f (x1) <f (x2).
所以f (x)在上也是增函数.
…………2分
（2）由（1）知，函数f (x)在
上是增函数.
…………1分
∵f (x)为奇函数，
∴
…………2分
由（1）知f (x)在
上是增函数，
∴
.
…………3分
∵
R，∴当sin
＝1时，
取得最大值
.
∵不等式恒成立，
∴故实数m的取值范围是
. ;
…………2分
22. （14分）（1）配方得f (A，B) = (sin2A-
)2 + (cos2B-
)2 +1， …………2分
∴ [f (A，B) ]min
= 1, 当且仅当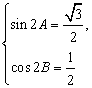
时取得最小值.
…………2分
在△ABC中，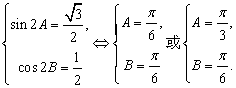
故C = 
或
.…………3分
（2）
A+B = ，于是
h（A）＝
＝cos2A－
＋3=2cos(2A+
) + 3.
…………4分
∵A+B = ，∴
.
…………1分
（3）∵函数h（A）在区间
上是减函数，在区间
上是增函数；而函数
在区间
上是减函数.
∴函数h（A）的图象与函数
的图象不相同，从而不存在满足条件的
向量p. …………2分
23．（14分）（1）∵，∴
，
于是an＋1＝Sn＋1－Sn＝（2 an＋1－2）－（2 an－2），即an＋1＝2an. …………2分
又a1＝S1＝2 a1－2, 得a1＝2. …………1分
∴是首项和公比都是2的等比数列，故an＝2n.
…………1分
(2) 由a1b1＝（2×1－1）×21＋1＋2＝6及a1＝2得b1＝3. …………1分
当
时，
，
∴
.
…………2分
∵an＝2n，∴bn＝2n＋1（）.
…………1分
∴
…………1分
（3）
. …………3分
.
…………2分