如皋市2006届高三数学综合测试
一、选择题:每小题5分,共12小题,共60分.在每小题的四个选项中,只有一项是符合要求的.
1.
已知集合![]() ,若
,若![]() ,则
,则![]() 的值为( )
的值为( )
A.1 B.2 C.1或2 D.不为零的任意实数
2. 下列函数中周期是2的函数是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3. 下列命题中正确的是( )
A.若直线![]() ∥平面M,则直线
∥平面M,则直线![]() 的垂线必平行于平面M;
的垂线必平行于平面M;
B.若直线![]() 与平面M相交,则有且只有一个平面经过
与平面M相交,则有且只有一个平面经过![]() 且与平面M垂直;
且与平面M垂直;
C.若直线![]() 平面M,
平面M,![]() 相交,且直线
相交,且直线![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,则
,则![]() ⊥M;
⊥M;
D.若直线![]() ∥平面M,直线
∥平面M,直线![]() ⊥
⊥![]() ,则
,则![]() ⊥M.
⊥M.
4.
已知![]() 展开式中常数项为1120,其中实数
展开式中常数项为1120,其中实数![]() 是常数,则展开式中各项系数的和为(
)
是常数,则展开式中各项系数的和为(
)
 A.
A.![]() B.
B.![]() C.1或
C.1或![]() D.1或
D.1或![]()
5.
若函数![]() 的图象的顶点在第四象限,则函数
的图象的顶点在第四象限,则函数![]() 的图象是( )
的图象是( )
A B C D
6.
已知实数![]() 满足
满足![]() .
.
命题P:函数![]() 在区间[0,1]上是减函数.
在区间[0,1]上是减函数.
命题Q:![]() 是
是![]() 的充分不必要条件.则( )
的充分不必要条件.则( )
A.“P或Q”为真命题; B.“P且Q”为假命题;
C.“┐P且Q”为真命题; D.“┐P或┐Q”为真命题
7. 已知两个点M(--5,0)和N(5,0),若直线上存在点P,使PM--PN=6,则称该直线为“B型直线”.给出下列直线①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中为“B型直线”的是( )
.其中为“B型直线”的是( )
A.①③ B.①② C.③④ D.①④
8.
在数列{![]() }中,
}中,![]() ,
,![]() (
(![]() ),则
),则![]() 为( )
为( )
A.34 B.36 C.38 D.40
9.
已知点B![]() ,点O为坐标原点,点A在圆
,点O为坐标原点,点A在圆![]() 上,则向量
上,则向量
![]() 的夹角
的夹角![]() 的最大值与最小值分别为( )
的最大值与最小值分别为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.设函数![]() 为定义域在R上的以3为周期的奇函数,若
为定义域在R上的以3为周期的奇函数,若![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.某商场宣传在“五一黄金周”期间对顾客购物实行一定的优惠,商场规定:
①如一次性购物不超过200元,不予以折扣;
②如一次性购物超过200元但不超过500元的,按标价给予九折优惠;
③如一次性购物超过500元的,其中500元给予9折优惠,超过500元的部分给予八五折优惠.
某人两次去购物,分别付款176元和432元,如果他只去一次购买同样的商品,则应付款( )
A.608元 B.574.1元 C.582.6元 D.456.8元
12.已知直线![]() (
(![]() 不全为0)与圆
不全为0)与圆![]() 的公共点,且公共点的横、纵坐标均为整数,那么这样的直线共有( )
的公共点,且公共点的横、纵坐标均为整数,那么这样的直线共有( )
A.66条 B.72条 C.74条 D.78条
二、填空题:每小题4分,共4小题,共计16分.将答案填在题中的横线上.
13.已知函数![]() 是R上的减函数,A(0,--3),B(--2,3)是其图象上的两点,那么不等式
是R上的减函数,A(0,--3),B(--2,3)是其图象上的两点,那么不等式
![]() 的解集是______________.
的解集是______________.
14.从4名男生和2名女生中任选3人参加演讲比赛,则所选3人中至少有1名女生的概率是______.15.双曲线![]() 的两个焦点为F1,F2,P在双曲线上,且满足PF1+PF2=
的两个焦点为F1,F2,P在双曲线上,且满足PF1+PF2=![]() ,则⊿PF1F2的面积为____________.
,则⊿PF1F2的面积为____________.
16.有一个正四棱锥,它的底面边长和侧棱长均为![]() ,现在要用一张正方形的包装纸将它完全包住.(不能裁剪纸,但可以折叠)那么包装纸的最小边长应为__________________.
,现在要用一张正方形的包装纸将它完全包住.(不能裁剪纸,但可以折叠)那么包装纸的最小边长应为__________________.
三、解答题:共6大题,共计74分,解答应写出文字说明、证明过程或演算步骤.
17.本题满分12分)
已知在⊿ABC中,角A、B、C的对边为![]() ,向量
,向量![]() ,
,
![]() ,
,![]() ⊥
⊥![]() .
.
(1)求角C.
(2)若![]() ,试求
,试求![]() 的值.
的值.
18.(本题满分12分)
 粒子A位于数轴
粒子A位于数轴![]() 处,粒子B位于
处,粒子B位于![]() 处,这两粒子每隔1秒向左或向右移动一个单位,设向右移动的概率为
处,这两粒子每隔1秒向左或向右移动一个单位,设向右移动的概率为![]() ,向左移的概率为
,向左移的概率为![]() .
.
(1)求第三秒时,粒子A在点![]() 处的概率.
处的概率.
(2)求第2秒时,粒子A、B同在点![]() 处的概率.
处的概率.
19.(本题满分12分)
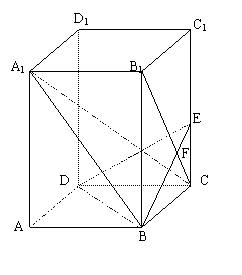
已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,
侧棱BB1=4,过点B作B1C的垂线交侧棱CC1于点E,
交B1C于点F,
(1)求证:A1C⊥平面BED;
(2)求A1B与平面BDE所成角的正弦值.
20.(本题满分12分)
已知函数![]() .
.
(1)将函数![]() 的图象向右平移两个单位,得到函数
的图象向右平移两个单位,得到函数![]() ,求
,求![]() 的解析式.
的解析式.
(2)函数![]() 与函数
与函数![]() 的图象关于直线
的图象关于直线![]() 对称,求
对称,求![]() 的解析式;
的解析式;
(3)设![]() ,
,![]() 的最小值是
的最小值是![]() ,且
,且![]() .求实数
.求实数![]() 的取值范围.
的取值范围.
 21.(本题满分12分)
21.(本题满分12分)
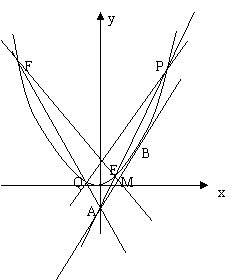
自点A(0,-1)向抛物线C:![]() 作切线AB,切点为B,且B在第一象限,再过线段AB的中点M作直线
作切线AB,切点为B,且B在第一象限,再过线段AB的中点M作直线![]() 与抛物线C交于不同的两点E、F.直线AF、AE分别交抛物线C于P、Q两点.
与抛物线C交于不同的两点E、F.直线AF、AE分别交抛物线C于P、Q两点.
(1)求切线AB的方程及切点B的坐标.
(2)证明![]() .
.
22.(本题满分14分)由原点O向三次曲线 ![]()
引切线,切点为P1![]() (O,P1两点不重合),再由P1引此
(O,P1两点不重合),再由P1引此
曲线的切线,切于点P2![]() (P1,P2不重合),如此继续下
(P1,P2不重合),如此继续下
去,得到点列:![]() .
.
(1)求![]() ;
;
(2)求![]() 与
与![]() 满足的关系式;
满足的关系式;
(3)若![]() ,试判断
,试判断![]() 与
与![]() 的大小关系,并说明理由.
的大小关系,并说明理由.
参考答案
一、选择题(每小题5分,共12小题,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | C | C | C | A | A | B | C | C | D | C | B |
二、填空题(每小题4分,共4小题,共计16分)
13.![]() 14.0.8 15.1 16.
14.0.8 15.1 16.![]()
三、解答题:(共6大题,共计74分)
14.(本题满分12分)
解:(1)由![]() 得
得![]()
![]()
![]() 即
即![]()
因为![]() ,所以
,所以![]() .
.
(2)因为![]()
![]() .(因为
.(因为![]() )
)
15.(本题满分12分)
解:(1)依题意有粒子A有以下三种走法:右右左,右右左、左右右,其概率为
![]() .
.
(2)粒子A只能为:右右走法,其概率为![]() ,粒子B有两种走法:右左、左右,其概率为
,粒子B有两种走法:右左、左右,其概率为![]() ,则粒子A、B同在
,则粒子A、B同在![]() 处的概率是
处的概率是![]() .
.
16.(本题满分12分)
解法一
(1)证明:连AC交DB于点O,
由正四棱柱性质可知AA1⊥底面ABCD,AC⊥BD,∴A1C⊥BD,
又∵A1B1⊥侧面BC1且BC1⊥BE ∴A1C⊥BE,
又∵BD∩BE=B,∴A1C⊥平面BDE.
(2)设A1C交平面BDE于点K,连结BK,则∠A1BK为A1B与平面BDE所成的角
在侧面BC1中,BE⊥B1C∴⊿BCE∽⊿B1BC
∴![]() 又BC=2,BB1=4,∴CE=1.
又BC=2,BB1=4,∴CE=1.
连OE,则OE为平面ACC1A1与平面BDE的交线,∴OE∩A1C=K
在Rt⊿ECO中,![]() ,∴
,∴![]()
又![]() ∵
∵![]()
又![]() ,∴
,∴![]()
在Rt⊿A1BK中,![]() ,即为A1B与平面BDE所成的角的正弦值.
,即为A1B与平面BDE所成的角的正弦值.
解法二:
(1)以D为原点,DA、DC、DD1所在的直线分别为x,y,z轴建立空间直角坐标系![]() .
.
D(0,0,0), A(2,0,0),B(2,2,0),C(0,2,0)
A1(2,0,4),B1(2,2,4),C1(0,2,4),D1(0,0,4),
设点E(0,2,t)
∵BE⊥B1C,∴![]()
![]() ,∴E(0,2,1)
,∴E(0,2,1)
又![]() ,
,![]() ,
,![]()
∴![]()
∴A1C⊥DB,且A1C⊥BE,∴A1C⊥平面BDE.
(2)设A1C∩平面BDE=K
则![]()
∴![]()
∴![]()
由![]() ⊥
⊥ ![]() 得
得![]()
∴![]() ,…………①
,…………①
![]() 同理有
同理有![]()
![]() 得
得![]()
…②
由①②联立,解得![]() ∴
∴![]()
∴![]() ,又易知
,又易知![]()
∴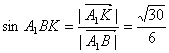 ,即所求角的正弦值为
,即所求角的正弦值为![]() .
.
20.(本题满分12分)
解:(1)易得![]() .
.
(2)设P![]() 为
为![]() 的图像上任一点,点P关于直线
的图像上任一点,点P关于直线![]() 的对称点为
的对称点为![]()
∵点![]() 在
在![]() 的图像上,
的图像上,
∴![]() ,即得
,即得![]() .
.
(3)![]()
![]()
下面求![]() 的最小值.
的最小值.
①当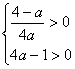 ,即
,即![]() 时
时![]()
由![]() ,得
,得![]() ,所以
,所以![]() .
.
②当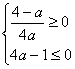 即
即![]() 时
时![]() 在R上是增函数,无最小值,与
在R上是增函数,无最小值,与![]() 不符.
不符.
③当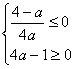 即
即![]() 时,
时,![]() 在R上是减函数,无最小值,与
在R上是减函数,无最小值,与![]() 不符.
不符.
④当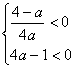 即
即![]() 时,
时,![]() ,与最小值
,与最小值![]() 不符.
不符.
综上所述,所求![]() 的取值范围是
的取值范围是![]() .
.
21.(本题满分12分)
解:(1)设切线AB的方程为![]() ,
,
代入![]() 得
得![]() ,由
,由![]() 得
得![]() ,AB的方程为
,AB的方程为![]() ,
,
易得切点B(1,1).
(2)线段AB的中点M![]() ,设过点M的直线
,设过点M的直线![]() 的方程为
的方程为![]() ,与
,与![]() 交于
交于![]()
由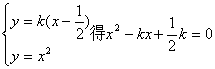 ,有
,有![]() .
.
再设P![]() ,Q
,Q![]() ,要证
,要证![]() ,只要PQ∥AB,证
,只要PQ∥AB,证![]() 即可.
即可.
由![]() .
.
∵A、P、F三点共线,有![]() ,∴
,∴![]()
![]() ,∴
,∴![]() ,又
,又![]() ∴
∴![]()
同理由A、E、Q三点共线得![]()
∴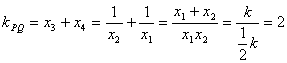
所以PQ∥AB,有![]() .
.
22.(本题满分14分)
解:(1)由![]() 得
得![]()
过曲线上的点P1![]() 的切线L1的方程为
的切线L1的方程为![]()
又∵切线L1过原点O,有![]()
化得![]() .
.
(2)过曲线上的点![]() 处的切线
处的切线![]() 方程为
方程为
![]()
![]() 过点
过点![]() 得
得![]()
由于![]() ,分解因式并约简,得
,分解因式并约简,得![]()
∴![]()
![]()
∴![]() .
.
(3)由(2)得:![]() ,∴
,∴![]()
故有数列![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列.
的等比数列.
∴![]() ,∴
,∴![]()
∵![]() ,∴当
,∴当![]() 为偶数时,
为偶数时,![]() ;当
;当![]() 为奇数时
为奇数时![]() .
.