2006届45分钟小测试卷（三角部分）（Ⅱ）
试卷总分100分 班级 姓名 座号 成绩
一、选择题：(本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的，将正确答案填入题号前.)
1.下列函数中，最小正周期为
的是 A．
B．
C．
D．
2.将函数
的图象向左平移
个单位，得到
的图象，则
等于
A．
B．
C．
D．
3.下列命题中正确的是 A．
为增函数 B．
在第一象限为增函数
C．
为奇函数 D．的反函数为
4.
单调增区间为 A．
B．
C．
D．
5 . 函数y = - xcosx的部分图象是
 |
6.
（A＞0，ω＞0）在x=1处取最大值，则A．
一定是奇函数 B．一定是偶函数 C．
一定是奇函数 D．一定是偶函数
7.已知
为奇函数，则的一个取值 A．0 B．π C． D．
8.
的图象中相邻的两条对称轴间距离为 A．3π B．
C．
D．
9．设
,且
,则
A．
B．
C．
D． 
10． 使
（ω＞0）在区间[0，1]至少出现2次最大值，则ω的最小值为
A．
B．
C．π D．
二.填空题(本大题共4小题，每小题4分，共16分。把答案填在题中横线上。)
11．把函数y = cos(x+)的图象向左平移m个单位(m>0), 所得图象关于y轴对称, 则m的最小值是_________。
12．函数y = -2sin(4x+
)的图象与x轴的交点中, 离原点最近的一点的坐标是_______。
13．
的图象关于
对称，则a等于___________。
14．①存在
使
②存在区间（a，b）使
为减函数而
＜0
③在其定义域内为增函数 ④
既有最大、最小值，又是偶函数
⑤
最小正周期为π 以上命题错误的为____________。
三. 解答题 (本大题共3小题，共34分，解答应写出文字说明，或演算步骤)
15．（本小题满分10分）函数
最小正周期为π，最大值为3，且
≠0），求f (x)的的解析式。
16．（本小题满分12分）求
的最小正周期、最大值、最小值
17．（本小题满分12分）
（ω＞0） （1）若f (x +θ)是周期为2π的偶函数，求ω及θ值 （2）f (x)在（0，）上是增函数，求ω最大值。
2006届45分钟小测试卷（三角部分）（Ⅱ）参考答案
一
选择题: 1. B [解析]：正弦、余弦型最小正周期为T=
，正切型最小正周期为T=
２.C [解析]：函数的图象向左平移个单位，得到
的图象，故
３.C [解析]：A、B、D都是定义域的问题
而
，故选C
４.B [解析]：∵=
∴要求单调增区间就是解
∴
５.D [解析]：∵函数y = - xcosx是奇函数，∴排除A、C，又当x取一个小正数时,y的值为负，选D
6. D [解析]： ∵（A＞0，ω＞0）在x=1处取最大值
∴在x=0处取最大值, 即y轴是函数的对称轴 ∴函数是偶函数
7.D [解析]：∵为奇函数
而=
∴的一个取值为
8.C [解析]： ∵=
∴图象的对称轴为
，即
故 相邻的两条对称轴间距离为
9. C [解析]：由
= 
= sinx-cosx = sinx – cosx 得
sinx ＞ cosx 又 ∵ ∴ 故选 C
10.A [解析]：要使（ω＞0）在区间[0，1]至少出现2次最大值
只需要最小正周期
1, 故
二填空题: 11．
π [解析]：把函数y = cos(x+)的图象向左平移m个单位(m>0),
得到图象y = cos(x++m)，而此图象关于y轴对称 故m的最小值是π
12.．
(, 0) [解析]：∵函数y = -2sin(4x+)的图象与x轴的相交
∴4x+=
， ∴
当k=1时，交点离原点最近，坐标为(, 0)。
13．－1 [解析]：的图象关于对称，则
即a =
14．①②③⑤ [解析]：①当时
，故①错 ②若为减函数则
，此时>0，故②错 ③当x分别去
时，y都是0，故③错
④∵=
∴既有最大、最小值，又是偶函数，故④对
⑤最小正周期为
，故⑤错
三解答题: 15．解：=
又最小正周期为π，最大值为3，且≠0），故
，
+1=3，
解得
因此
16．解：
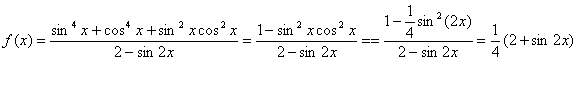故最小正周期、最大值、最小值分别为
17．解： 因为f (x +θ)=
又f (x
+θ)是周期为2π的偶函数，
故
Z
（2）因为f (x)在（0，）上是增函数，故ω最大值为