|
|
汕头市2004年普通高校招生模拟考试
数 学
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ卷1至2页。第Ⅱ卷3至10页。考试结束后，将本试卷和答题卡一并交回。
第Ⅰ卷 (选择题 共60分)
注意事项：
1.答第一卷前，考生务必将自己的姓名、准考号、考试科目用铅笔涂写在答题卡上。
2.每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦
干净后，再选涂其它答案，不能答在试题卷上。
 |
一．选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．
（1）已知向量a＝
，b＝
，且(a＋
b)⊥(a－b)，则等于
（A）1 （B）－1 （C）3 （D）－3
（2）如果森林区的森林蓄积量每年平均比上一年增长10.4％，那么经过x年可以增长到原来
的y倍，则函数
的图象大致为
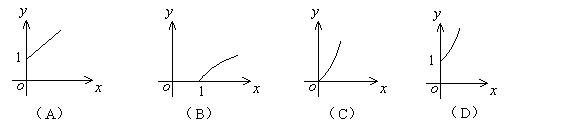
（3）若3个平面将空间分成m部分，则m的值为
（A）4 （B）4或6 （C）4或6或7 （D）4或6或7或8
（4）同一天内，甲地下雨的概率是0.15，乙地下雨的概率是0.12，假定在这天两地是否下雨
相互之间没有影响，那么甲、乙两地都不下雨的概率是
（A）0.102 （B）0.132 （C）0.748 （D）0.982
（5）已知F是抛物线
的焦点，P是该抛物线上的动点，则线段PF中点的轨迹方程是
（A）
（B）
（C）
（D）
（6）已知条件p：
＞2，条件q：5x－6＞
，则
是
的
（A）充分必要条件 （B）充分非必要条件
（C）必要非充分条件 （D）既非充分又非必要条件
（7）直线
与圆
在第一象限内有两个不同的交点，则m的取值范围是
（A）1＜m＜2 （B）
＜m＜3 （C）1＜m＜ （D）＜m＜2
（8）已知函数
在区间
上是增函数，则实数a的取值范围是
（A）
（B）
（C）
（D）
（9）若x＞4，则函数
（A）有最大值—6 （B）有最小值6 （C）有最大值—2 （D）有最小值2
（10）设球O的半径为R，A、B、C为球面上三点，A与B、A与C的球面距离都为
，B与C的球面距离为
，则球O在二面角B—OA—C内的那一部分的体积是
（A）
（B）
（C）
（D）
（11）将函数
的图象按向量a＝
平移，得到函数
的图象，那么
函数
是
（A）
（B）
（C）
（D）
（12）已知符号函数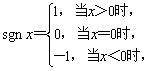
则方程
的所有解之和是
（A）0
（B）2
（C）
（D）
汕头市2004年普通高校招生模拟考试
数 学
第Ⅱ卷 (非选择题 共90分)
注意事项：
1. 用钢笔或圆珠笔直接答在试题中。
2. 答卷前将密封线内的项目填写清楚。
| 题 号 | 二 | 三 | 总 分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | |||
| 分 数 | ||||||||
| 得分 | 评卷人 |
|
|
二．填空题：本大题共4小题，每小题4分，共16分．把答案填在题中横线上．
（13）i为虚数单位，复数
等于___________________．
（14）求极限：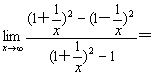
____________________．
（15）已知
的展开式中
的系数为9，则常数a的值为_______________．
（16）已知函数
给出下列四个结论：
① 当且仅当
时取得最小值；
② 是周期函数；
③ 的值域是
；
④ 当且仅当
时
．
其中正确结论的序号是：___________________________．
三．解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤．
| 得分 | 评卷人 |
|
|
（17）（本小题满分12分）
编号为1、2、3的三位学生随意入座编号为1、2、3的三个座位，每位学生坐一个座位，设与座位编号相同的学生的个数是
．
（Ⅰ）求随机变量的概率分布；
（Ⅱ）求随机变量的数学期望和方差．
| 得分 | 评卷人 |
|
|
（18）（本小题满分12分）
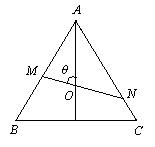
如图，已知在等边△ABC中，AB＝3，O为中心，过O的直线交AB于M，AC于N，设
∠AOM＝
(60°≤≤120°)，当分别为何值时，
取得最大值和最小值．
| 得分 | 评卷人 |
|
|
（19）（本小题满分12分）
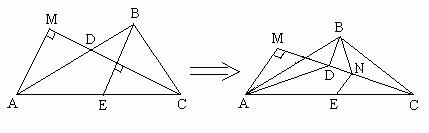
在△ABC中，CD为∠C的平分线，AC＝4，BC＝2，过B作BN⊥CD于N，延长
BN交CA于E，作AM⊥CD，交CD的延长线于M，将图形沿CD折起，使∠BNE
＝120°．求：
（Ⅰ）折起后AM与BC所成的角；
（Ⅱ）折起后所得的线段AB的长度．
| 得分 | 评卷人 |
|
|
（20）（本小题满分14分）
已知数列
的通项为
，前n项和为
，且是与2的等差中项；数列
中，
＝1，点
在直线x－y＋2＝0上．
（Ⅰ）求数列、的通项公式；
（Ⅱ）设的前n项和为
，试比较
与2的大小；
（Ⅲ）设
，求
的最小整数c．
| 得分 | 评卷人 |
|
|
（21）（本小题满分12分）
一条斜率为1的直线l与离心率为的双曲线
交于P、Q两点，
直线l与y轴交于R点，且
，求直线与双曲线的方程．
| 得分 | 评卷人 |
|
|
（22）（本小题满分12分）
已知函数
．
（Ⅰ）若x＞1，求证：
；
（Ⅱ）是否存在实数k，使方程
有四个不同的实根？若存在，
求出k的取值范围；若不存在，说明理由．
