2005学年第一学期高三质量调研测试
数 学 试 卷
考生注意:
1. 答卷前,考生务必将学校、班级、学号、姓名等填写清楚.
2. 本试卷共有22道题,满分150分,考试时间120分钟.请考生用钢笔或圆珠笔书写,请不要将答案写在试卷的密封线以内.
3. 使用新教材的考生请注意符号说明:
| 符号意义 | 本试卷所用符号 | 等同于新教材符号 |
| 向量 |
|
|
| 正切 |
|
|
| 题 号 | 一 | 二 | 三 | 总 分 | |||||||||
| 1-12 | 13-16 | 17 | 18 | 19 | 20 | 21 | 22 | ||||||
| 得 分 | |||||||||||||
一.填空题(本大题满分48分)本大题共有12题,只要求直接填写结果,每个空格填对得4分,否则一律得零分.
1.设角![]() 的终边过点
的终边过点![]() ,则
,则![]() ______________.
______________.
2.![]() (
(![]() 为虚数单位)的运算结果是_______________.
为虚数单位)的运算结果是_______________.
3.不等式![]() 的解是__________________________.
的解是__________________________.
4.设![]() 是定义在
是定义在![]() 上的奇函数,则
上的奇函数,则![]() 的图像过定点_________________.
的图像过定点_________________.
5.已知函数![]() ,则
,则![]() _______________.
_______________.
6.计算:![]() =_______________.
=_______________.
7.设函数![]() 满足:对任意的
满足:对任意的![]() ,都有
,都有![]() ,则
,则![]() 与
与![]() 的大小关系是______________________.
的大小关系是______________________.
8.等差数列![]() 中,
中,![]() ,则
,则![]() ____________.
____________.
9.矩形的面积与其周长的数值相等,则矩形面积的最小值是___________.
10.关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,则复数
,则复数![]() 所对应的点位于复平面内的第________象限.
所对应的点位于复平面内的第________象限.
11.函数![]() 图像上至少存在不同的三点到原点的距离构成等比数列,则公比的取值范围是_________________________.
图像上至少存在不同的三点到原点的距离构成等比数列,则公比的取值范围是_________________________.
12.在一次产品质量抽查中,某批次产品被抽出10件样品进行检验,其中恰有两件不合格品.如果对这10件样品逐个进行检验,则这两件不合格品恰好在第五次被全部检出的概率是______________(结果用最简分数表示).
二.选择题(本大题满分16分)本大题共有4题,每题都给出代号为A、B、C、D的四个结论,其中有且只有一个结论是正确的,必须把正确的代号写在题后的圆括号内,选对得4分,不选、选错或者选出的代号超过一个(不论是否都写在圆括号内),一律得零分.
13.设![]() 是两个非零向量,则“
是两个非零向量,则“![]() ”是“
”是“![]() ”成立的
”成立的
A.充要条件. B.必要不充分条件.
C.充分不必要条件. D.既不充分也不必要条件.
14.![]() 内角分别是
内角分别是![]() ,若关于
,若关于![]() 的方程
的方程![]() 有一个根为1,则
有一个根为1,则![]() 一定是
一定是
A.等腰直角三角形. B.直角三角形.
C.等腰三角形. D.等边三角形.
15.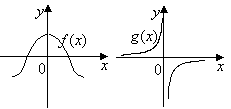 设函数
设函数![]() 与函数
与函数![]() 的图像
的图像
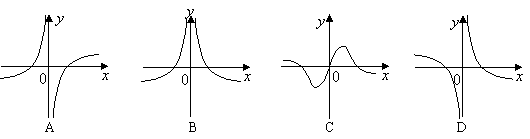 如右图所示,则函数
如右图所示,则函数![]() 的图
的图
像可能是下面的
16.若不等式![]() 对于任意正整数
对于任意正整数![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是
的取值范围是
A.![]() . B.
. B.![]() .
.
C.![]() .
D.
.
D.![]() .
.
三. 解答题(本大题满分86分)本大题共有6题,解答下列各题必须写出必要的步骤.
17.(本题满分12分)
已知复数![]() 是实系数一元二次方程
是实系数一元二次方程![]() 的一个根,向量
的一个根,向量![]() 、
、![]() ,求实数
,求实数![]() 和
和![]() 使得
使得![]() .
.
18.(本题满分12分)
设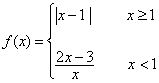 ,解不等式
,解不等式![]() .
.
19.(本题满分14分)本题共有2个小题,每小题满分各7分.
已知![]() 三个顶点分别是A(3,0)、B(0,3)、C
三个顶点分别是A(3,0)、B(0,3)、C![]() ,
,
其中![]() .
.
(1)若![]() ,求角
,求角![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值.
的值.
20.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
为了缓解交通压力,某省在两个城市之间特修一条专用铁路,用一列火车作为公共交通车.如果该列火车每次拖4节车厢,每日能来回16趟;如果每次拖7节车厢,则每日能来回10趟.火车每日每次拖挂车厢的节数是相同的,每日来回趟数y是每次拖挂车厢节数x的一次函数,每节车厢满载时能载客110人.
(1) 求出y关于x的函数关系式;
(2) 这列火车满载时每次应拖挂多少节车厢才能使每日营运人数最多?并求出每天最多的营运人数.
21.(本满分16分)本题共有3个小题,第1、3小题满分各5分,第2小题满分6分.
如果一个数列的各项都是实数,且从第二项开始,每一项与它前一项的平方差是相同的常数,则称该数列为等方差数列,这个常数叫这个数列的公方差.
(1)设数列![]() 是公方差为
是公方差为![]() 的等方差数列,求
的等方差数列,求![]() 和
和![]()
![]() 的关系式;
的关系式;
(2)若数列![]() 既是等方差数列,又是等差数列,证明该数列为常数列;
既是等方差数列,又是等差数列,证明该数列为常数列;
(3) 设数列![]() 是首项为
是首项为![]() ,公方差为
,公方差为![]() 的等方差数列,若将
的等方差数列,若将![]() 这种顺
这种顺
序的排列作为某种密码,求这种密码的个数.
22.(本题满分18分)本题共有3个小题,第1小题满分5分,第2小题满分6分,
第3小题满分7分.
已知函数![]() ,当点
,当点![]() 在
在![]() 的图像上移动时,
的图像上移动时,
点![]() 在函数
在函数![]() 的图像上移动.
的图像上移动.
(1) 若点P坐标为(![]() ),点Q也在
),点Q也在![]() 的图像上,求
的图像上,求![]() 的值;
的值;
(2) 求函数![]() 的解析式;
的解析式;
(3) 当![]() 时,试探求一个函数
时,试探求一个函数![]() 使得
使得![]() 在限定定义域为
在限定定义域为
![]() 时有最小值而没有最大值.
时有最小值而没有最大值.
2005学年第一学期高三质量调研测试数学试卷
参考答案及评分标准
一.(第1至12题)每一题正确的得4分,否则一律得零分.
1.![]() .
2.
.
2.![]() .
3.
.
3.![]() .
4.
.
4.![]() .
.
5.![]() .
6.
.
6.![]() .
7.
.
7.![]() . 8.
. 8.![]() .
.
9.![]() .
10.二.
11.
.
10.二.
11.![]() . 12.
. 12.![]() .
.
二.(第13至16题)每一题正确的得4分,否则一律得零分.
13.C . 14.B . 15.A . 16.C .
三.(第17至22题)
17.(本题满分12分)解:∵![]() 是实系数一元二次方程
是实系数一元二次方程![]() 的一个根,
的一个根,
∴![]() 也是方程
也是方程![]() 的根…………………………………………3分
的根…………………………………………3分
∴![]() ,
,![]() ……………………7分
……………………7分
故![]() 由
由![]() 得
得 ![]() ,………9分
,………9分
∴![]() , ∴
, ∴![]() ,
,![]() .……………………………………12分
.……………………………………12分
18.(本题满分12分)
解:(1)当![]() 时,原不等式等价于
时,原不等式等价于![]() ,即
,即![]() 或
或![]() ……3分
……3分
∴![]() . ………………………………………………5分
. ………………………………………………5分
(2)当![]() 时,原不等式等价于
时,原不等式等价于![]() ,即
,即![]() 或
或![]() …………8分
…………8分
∴![]() . …………………………………………………10分
. …………………………………………………10分
综上所述,不等式![]() 的解集为
的解集为![]() . ……12分
. ……12分
19.(本题满分14分)
解:(1)∵![]() 三个顶点分别是A(3,0)、B(0,3)、C
三个顶点分别是A(3,0)、B(0,3)、C![]() ,
,
∴![]() ,
,![]() …………2分
…………2分
由![]() 得,
得,![]() ……4分
……4分
即 ![]() ………………………………6分
………………………………6分
∵
![]() , ∴
, ∴ ![]() .…………………………………………7分
.…………………………………………7分
(2)由![]() 得,
得,![]() ……9分
……9分
即 ![]() , ………………………………………………………10分
, ………………………………………………………10分
∴
![]() ,
,![]() ……11分
……11分
又 ![]() , ∴
, ∴![]() ,
,![]() ………………………12分
………………………12分
![]()
∴ ![]() . ……………………………………………………14分
. ……………………………………………………14分
20.(本题满分14分)
解:(1)依题意,设![]() ,则
,则![]() ,解得
,解得![]() , ……………4分
, ……………4分
∴![]() 为所求.(未注明定义域,不扣分) ……6分
为所求.(未注明定义域,不扣分) ……6分
(2)该列火车满载时每日的营运人数为
![]() ……………………………………………9分
……………………………………………9分
![]() (当且仅当
(当且仅当![]() 时取等号) ……………12分
时取等号) ……………12分
(用二次函数求解的请相应给分)
故这列火车满载时每次应拖挂![]() 节车厢才能使每日营运人数最多,最多营运
节车厢才能使每日营运人数最多,最多营运
人数为![]() 人.
……………………………………………………………14分
人.
……………………………………………………………14分
21.(本满分16分)
(1)解:由等方差数列的定义可知:![]()
![]() ………………5分
………………5分
(2)证法一:∵![]() 是等差数列,设公差为
是等差数列,设公差为![]() ,则
,则![]()
又![]() 是等方差数列,∴
是等方差数列,∴![]() ………………………………7分
………………………………7分
∴ ![]()
即![]() , …………………………………10分
, …………………………………10分
∴![]() ,即
,即![]() 是常数列.…………………………………………………11分
是常数列.…………………………………………………11分
证法二:∵![]() 是等差数列,设公差为
是等差数列,设公差为![]() ,则
,则![]() ……1
……1
又![]() 是等方差数列,设公方差为
是等方差数列,设公方差为![]() ,则
,则![]() ……2…………7分
……2…………7分
1代入2得,![]() ……3
……3
同理有,![]() ……4
……4
两式相减得:即![]() ,…………………………………10分
,…………………………………10分
∴![]() ,即
,即![]() 是常数列.………………………………………………11分
是常数列.………………………………………………11分
证法三:(接证法二1、2)
由1、2得出:若![]() ,则
,则![]() 是常数列 …………………8分
是常数列 …………………8分
若![]() , 则
, 则![]() 是常数, ∴
是常数, ∴![]() ,矛盾…………10分
,矛盾…………10分
∴ ![]() 是常数列.
…………………11分
是常数列.
…………………11分
(3)依题意, ![]()
![]() ,
,
![]() ,
,![]()
∴![]() ,或
,或![]() ,
……………………………13分
,
……………………………13分
即该密码的第一个数确定的方法数是![]() ,其余每个数都有“正”或“负”两种
,其余每个数都有“正”或“负”两种
确定方法,当每个数确定下来时,密码就确定了,即确定密码的方法数是![]() 种,
种,
故,这种密码共![]() 种.…………………………………………………16分
种.…………………………………………………16分
22.(本题满分18分)
解:(1)当点![]() 坐标为(
坐标为(![]() ),点
),点![]() 的坐标为
的坐标为![]() ,…………2分
,…………2分
∵点![]() 也在
也在![]() 的图像上,∴
的图像上,∴![]() ,即
,即![]() .……5分
.……5分
(根据函数![]() 的单调性求得
的单调性求得![]() ,请相应给分)
,请相应给分)
(2)设![]() 在
在![]() 的图像上
的图像上
则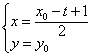 ,即
,即![]() ……………………………………8分
……………………………………8分
而![]() 在
在![]() 的图像上,∴
的图像上,∴![]()
代入得,![]() 为所求.…………………………………11分
为所求.…………………………………11分
(3)![]() ;或
;或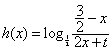 等. …………………15分
等. …………………15分
如:当![]() 时,
时,
![]()
![]()
![]()
∵![]() 在
在![]() 单调递减, ∴
单调递减, ∴![]() 故
故 ![]() ,
,
即![]() 有最小值
有最小值![]() ,但没有最大值.………………………18分
,但没有最大值.………………………18分
(其他答案请相应给分)
(参考思路)在探求![]() 时,要考虑以下因素:①
时,要考虑以下因素:①![]() 在
在![]() 上必须有意义(否则不能参加与
上必须有意义(否则不能参加与![]() 的和运算);②由于
的和运算);②由于![]() 和
和![]() 都是以
都是以![]() 为底的对数,所以构造的函数
为底的对数,所以构造的函数![]() 可以是以
可以是以![]() 为底的对数,这样与
为底的对数,这样与![]() 和
和![]() 进行的运算转化为真数的乘积运算;③以
进行的运算转化为真数的乘积运算;③以![]() 为底的对数是减函数,只有当真数取到最大值时,对数值才能取到最小值;④为方便起见,可以考虑通过乘积消去
为底的对数是减函数,只有当真数取到最大值时,对数值才能取到最小值;④为方便起见,可以考虑通过乘积消去![]() ;⑤乘积的结果可以是
;⑤乘积的结果可以是![]() 的二次函数,该二次函数的图像的对称轴应在直线
的二次函数,该二次函数的图像的对称轴应在直线![]() 的左侧(否则真数会有最小值,对数就有最大值了),考虑到该二次函数的图像与
的左侧(否则真数会有最小值,对数就有最大值了),考虑到该二次函数的图像与![]() 轴已有了一个公共点
轴已有了一个公共点![]() ,故对称轴又应该是
,故对称轴又应该是![]() 轴或在
轴或在![]() 轴的右侧(否则该二次函数的值在
轴的右侧(否则该二次函数的值在![]() 上的值不能恒为正数),即若抛物线与
上的值不能恒为正数),即若抛物线与![]() 轴的另一个公共点是
轴的另一个公共点是![]() ,则
,则![]() ,且抛物线开口向下.
,且抛物线开口向下.