上海市浦东新区2006届高三第一学期期末质量抽查数学试题2006.1
一、填空题：
1、
。
2、函数
的定义域为 
。
3、不等式
的解集为 
。
4、已知
，则
= 
。
5、计算：
。
6、函数
的反函数的图像经过
，则
。
7、若
，则
。
8、（理）在极坐标系中，
是极点，
，则
的形状为 等腰直角三角形 。
（文）某工程由下列工序组成，则工程总时数为 
天。
 |
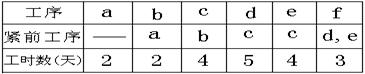9、有4条线段，长度分别为3，5，7，8，从这4条线段中任取3条，则所取3条线段能构成一个三角形的概率是
。
10、在中，
，
，
，则边
长为 
。
11、方程
的解的个数是 
个
。
12、有穷数列
，
为其前
项和，定义
为数列的“凯森和”。如果有99项的数列
的“凯森和”为
，则有
项的
的“凯森和”
。
二、选择题：
13、“
”是“
”的
（ 
）
A. 充分而不必要条件 B.必要而不充分条件 C. 充要条件 D.既不充分也不必要条件
14、复数
，则
在复平面内的对应点位于
（ D ）
A.第一象限 B. 第二象限 C. 第三象限 D. 第四象限
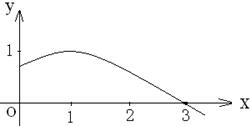15、函数
的部分图象如图，则
、
可以取的
一组值是 （ C ）
A、
B、
C、
D、
16、已知命题
：函数
的值域为
，命题
：
是减函数，若或为真命题，且为假命题，求实数
的取值范围是
（ D ）
A. 
B.
C.
D.
或
三、解答题：
17、关于
的方程
有一实根为,设复数
，
求
的值及复数
的模。
解：将代入方程，可知
，∴
， 
，∴
。
18、已知集合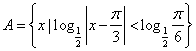
，求
解：A＝（－
，
）
，B＝
，∴=
。
19、先阅读下列不等式的证法，再解决后面的问题：
已知
，
，求证：
证明：构造函数
，
因为对一切
，恒有
成立，所以
，从而证得。
（1）若
，
，请写出上述结论的推广形式；
（2）参考上述解法，对你推广的结论加以证明。
解：（1）若，，则
。
（2）证明：构造函数
，
∵
，即
恒成立，
∴
，即。
20、现有一批货物用轮船从上海洋山深水港运往青岛，已知该船航行的最大速度为35海里/小时，上海至青岛的航行距离约为500海里，每小时运输成本由燃料费用和其余费用组成。轮船每小时使用的燃料费用与轮船速度的平方成正比（比例系数为0.6），其余费用每小时960元。
(1)把全程运输成本y(元)表示为速度（海里/小时）的函数；
(2)为了使全程运输成本最小，轮船应以多大速度行驶。
解：(1)
(
)
(2)先证明其在上为减函数，则
时，取得最小值。答：略。
21、已知在数列中，
（
）
(1)若
，求
；
(2)（理）若
是等比数列，且
是等差数列，求
满足的条件；
（文）
，若是等比数列，且是等差数列，求满足的关系式；
(3)一个质点从原点出发，依次按向右、向上、向左、向下的方向交替地运动，第次运动的位移是
，质点到达点
，设点
的横坐标为
，若
，求。
解：(1)∵
，∴
，
，猜测
。
(2)（理）
，当
＝0，显然成立；当
0，
，则
；
，当
，显然成立；当
，
。
（文），，。
(3)
，则
，∵
，∴
，
由
。
22、已知函数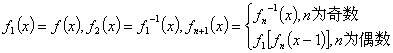
，
(1)若函数
，求函数
的解析式；
(2)（理）若函数
，函数
的定义域是
，求的值；
（文）若函数，求函数
的定义域；
(3)设
是定义在上的周期为4的奇函数，且函数的图像关于直线
对称，
当
，求正数的最小值及函数在
上的解析式。
解：(1)∵，
，∴
，
，
(2) （理）
，
∴的定义域是
，∴
，即
。
（文）
，函数的定义域是
。
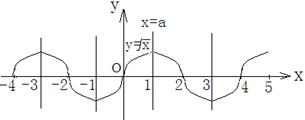(3) 据题意，作图如下：
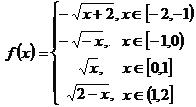可知正数
。
函数在上的解析式了
。