上海市普陀区2006届高三第一学期期末数学抽查
一、填空题:
1、函数![]() 的最小正周期是
的最小正周期是 ![]() 。
。
2、不等式![]() 的解集是
的解集是 ![]() 。
。
3、边长分别为![]() 的三角形的最大角的大小是
的三角形的最大角的大小是 ![]() 。
。
4、若函数![]() ,则方程
,则方程![]() 的解是
的解是 ![]() 。
。
5、若复数![]() 是纯虚数,则
是纯虚数,则![]()
![]() 。
。
6、过点![]() 且与直线
且与直线![]() 平行的直线的一般式方程是
平行的直线的一般式方程是 ![]() 。
。
7、已知![]() ,则
,则![]()
![]() (用含
(用含![]() 的代数式表示结果)。
的代数式表示结果)。
8、已知无穷等比数列![]() 的第二项
的第二项![]() ,各项和
,各项和![]() ,则该数列的公比
,则该数列的公比![]()
![]() 。
。
9、设![]() ,则
,则![]()
![]() 。
。
10、在圆![]() 上与直线
上与直线![]() 距离最小的点的坐标是
距离最小的点的坐标是 ![]() 。
。
11、我国男足运动员转会至海外俱乐部常会成为体育媒体关注的热点新闻。05年8月,在上海申花俱乐部队员杜威确认转会至苏超凯尔特人俱乐部之前,各种媒体就两俱乐部对于杜威的转会费协商过程纷纷“爆料”:
 媒体A:“……, 凯尔特人俱乐部出价已从80万英镑提高到了120万欧元。”
媒体A:“……, 凯尔特人俱乐部出价已从80万英镑提高到了120万欧元。”
媒体B:“……, 凯尔特人俱乐部出价从120万欧元提高到了100万美元,同
时增加了不少附加条件。”
媒体C:“……, 凯尔特人俱乐部出价从130万美元提高到了120万欧元。”
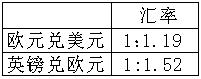
 请根据表中提供的汇率信息(由于短时间内国际货币的汇率变化不大,我们假定比值为定值),我们可以发现只有媒体
请根据表中提供的汇率信息(由于短时间内国际货币的汇率变化不大,我们假定比值为定值),我们可以发现只有媒体 ![]() (填入媒体的字母编号)的报道真实性强一些。
(填入媒体的字母编号)的报道真实性强一些。
12、如图,已知![]() 和
和![]() 都是正方形,且
都是正方形,且![]() ,
,![]() ,
,
若将图中已作出的线段的两个端点分别作为向量的始点和终点所形成的不相等的向量的全体
构成集合M,则从集合M中任取两个向量恰为平行向量的概率是 ![]() (用分数表示结果)。
(用分数表示结果)。
二、选择题:
13、设![]() 都是实数,则“
都是实数,则“![]() ”是“
”是“![]() ”的 条件
( A
)
”的 条件
( A
)
A,充分非必要; B,必要非充分; C,充要; D,既非充分又非必要。
14、已知等比数列![]() 中,
中,![]() ,且
,且![]() ,则
,则![]() (
B )
(
B )
A,![]() ;
B,
;
B,![]() ;
C,
;
C,![]() ;
D,
;
D,![]() 。
。
15、定义在![]() 上的函数
上的函数![]() 既是偶函数又是周期函数,若
既是偶函数又是周期函数,若![]() 的最小正周期是
的最小正周期是![]() ,且当
,且当![]() 时,
时,![]() ,则
,则![]() 的值为
( D
)
的值为
( D
)
A,![]() ;
B,
;
B,![]() ;
C,
;
C,![]() ;
D,
;
D,![]() 。
。
16、若方程![]() 表示双曲线,则下列方程所表示的椭圆中,与此双曲线有共同焦点的是 (
C )
表示双曲线,则下列方程所表示的椭圆中,与此双曲线有共同焦点的是 (
C )
A,![]() ; B,
; B,![]() ; C,
; C,![]() ; D,
; D,![]() 。
。
三、解答题:
17、已知:向量![]() ,求:
,求:![]() 。
。
解法一:由![]() ,又由条件得
,又由条件得![]() ,∴
,∴![]() ,
,
∴![]() 。
。
解法二:∵![]() ,
,
∴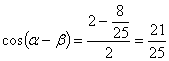 。
。
18、在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() 的焦点为
的焦点为![]() ,抛物线上一点
,抛物线上一点![]() 的横坐标为
的横坐标为![]() ,直线
,直线![]() 与抛物线交于点
与抛物线交于点![]() 、
、![]() ,求向量
,求向量![]() 和
和![]() 夹角的大小。
夹角的大小。
解:![]() ,由抛物线的对称性,不妨设
,由抛物线的对称性,不妨设![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,
,
把它代入![]() ,得
,得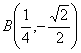 ,则
,则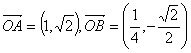 ,设向量
,设向量![]() 和
和![]() 夹角为
夹角为![]() ,
,
则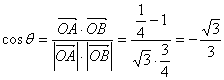 ,由对称性,当
,由对称性,当![]() 时,结论相同。
时,结论相同。
∴向量![]() 和
和![]() 夹角的大小为
夹角的大小为![]() 。
。
19、求证:不存在虚数![]() 同时满足:①
同时满足:①![]() ;②
;②![]() (
(![]() 为实数且
为实数且![]() )。
)。
解:假设存在虚数![]() 同时满足两个条件,
同时满足两个条件,
即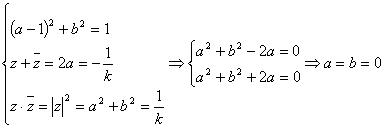 与假设
与假设![]() 矛盾,
矛盾,
∴不存在虚数![]() 同时满足①②两个条件。
同时满足①②两个条件。
20、人口问题其实是许多国家的政府都要面对的问题。05年10月24日出版的《环球时报》就报道了一篇俄罗斯政府目前遭遇“人口危机”的文章。报道中引用了以下来自俄政府公布的数据:
●截至05年6月底,俄罗斯人口为![]() 亿,人口密度每平方公里只有
亿,人口密度每平方公里只有![]() 人;
人;
●04年一年俄人口就减少了![]() 万,05年1月至5月共又减少了
万,05年1月至5月共又减少了![]() 万;
万;
●据俄联邦安全会议预测,到2050年,俄将只有约![]() 亿人口,比目前锐减
亿人口,比目前锐减![]() 。
。
试根据以上数据信息回答下列问题:
(1)以04年至05年5月这17个月平均每月人口减少的数据为基础,假设每月人口减少相同,预测到2050年6月底,俄罗斯的人口约为多少亿?(保留三位小数)
(2)按第(1)小题给定的预测方法,到何时俄罗斯的人口密度将低于每平方公里![]() 人?
人?
解:(1)由给出的信息可知,17个月里平均每月人口减少![]() 万人,
万人,
2005年6月底至2050年6月底共经过![]() 个月,若每月人口减少数相同,
个月,若每月人口减少数相同,
则到2050年6月底俄罗斯的人口数约为![]() 万,即约为
万,即约为![]() 亿。
亿。
(2)设从05年6月底起,经![]() 个月后俄罗斯的人口密度将低于每平方公里
个月后俄罗斯的人口密度将低于每平方公里![]() 人,
人,
于是有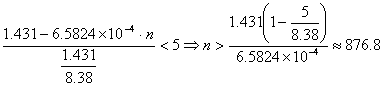 ,
,
∴至少要经过![]() 个月,即
个月,即![]() 年零
年零![]() 个月,也就是到2078年7月底,俄罗斯的人口密度将低于每平方公里
个月,也就是到2078年7月底,俄罗斯的人口密度将低于每平方公里![]() 人。
人。
21、设函数![]() ,函数
,函数![]() ,其中
,其中![]() 为常数且
为常数且![]() ,令函数
,令函数![]() 为函数
为函数![]() 和
和![]() 的积函数。
的积函数。
(1)求函数![]() 的表达式,并求其定义域;
的表达式,并求其定义域;
(2)当![]() 时,求函数
时,求函数![]() 的值域;
的值域;
(3)是否存在自然数![]() ,使得函数
,使得函数![]() 的值域恰为
的值域恰为![]() ?若存在,试写出所有满足条件的自然数
?若存在,试写出所有满足条件的自然数![]() 所构成的集合;若不存在,试说明理由。
所构成的集合;若不存在,试说明理由。
解:(1)![]() ,
,![]() 。
。
(2)∵![]() ,∴函数
,∴函数![]() 的定义域为
的定义域为![]() ,令
,令![]() ,则
,则![]() ,
,![]() ,
,
∴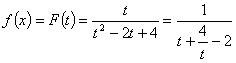 ,
,
∵![]() 时,
时,![]() ,又
,又![]() 时,
时,![]() 递减,∴
递减,∴![]() 单调递增,
单调递增,
∴![]() ,即函数
,即函数![]() 的值域为
的值域为![]() 。
。
(3)假设存在这样的自然数![]() 满足条件,令
满足条件,令![]() ,则
,则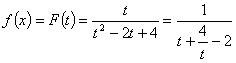 ,
,
∵![]() ,则
,则![]() ,要满足值域为
,要满足值域为![]() ,则要满足
,则要满足![]() ,
,
由于当且仅当![]()
![]() 时,有
时,有![]() 中的等号成立,且此时
中的等号成立,且此时![]() 恰为最大值,
恰为最大值,
∴![]() ,
,
又![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,∴
上是减函数,∴![]()
![]() ,
,
综上,得 ![]() 。
。
22、已知二次函数![]() 同时满足:①不等式
同时满足:①不等式![]() 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在![]() ,使得不等式
,使得不等式![]() 成立。
成立。
设数列![]() 的前
的前![]() 项和
项和![]() ,
,
(1)求数列![]() 的通项公式;
的通项公式;
(2)试构造一个数列![]() ,(写出
,(写出![]() 的一个通项公式)满足:对任意的正整数
的一个通项公式)满足:对任意的正整数![]() 都有
都有![]() ,且
,且![]() ,并说明理由;
,并说明理由;
(3)设各项均不为零的数列![]() 中,所有满足
中,所有满足![]() 的正整数
的正整数![]() 的个数称为这个数列
的个数称为这个数列![]() 的变号数。令
的变号数。令![]() (
(![]() 为正整数),求数列
为正整数),求数列![]() 的变号数。
的变号数。
解:(1)∵![]() 的解集有且只有一个元素,∴
的解集有且只有一个元素,∴![]() ,
,
当![]() 时,函数
时,函数![]() 在
在![]() 上递增,故不存在
上递增,故不存在![]() ,使得不等式
,使得不等式![]() 成立。
成立。
当![]() 时,函数
时,函数![]() 在
在![]() 上递减,故存在
上递减,故存在![]() ,使得不等式
,使得不等式![]() 成立。
成立。
![]() 综上,得
综上,得![]() ,
,![]() ,∴
,∴![]() ,∴
,∴
(2)要使![]() ,可构造数列
,可构造数列![]() ,∵对任意的正整数
,∵对任意的正整数![]() 都有
都有![]() ,
,
∴当![]() 时,
时,![]() 恒成立,即
恒成立,即![]() 恒成立,即
恒成立,即![]() ,
,
又![]() ,∴
,∴![]() ,∴
,∴![]() ,等等。
,等等。
(3)解法一:由题设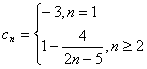 ,
,
∵![]() 时,
时,![]() ,∴
,∴![]() 时,数列
时,数列![]() 递增,
递增,
∵![]() ,由
,由![]() ,可知
,可知![]() ,即
,即![]() 时,有且只有
时,有且只有![]() 个变号数;
个变号数;
又∵![]() ,即
,即![]() ,∴此处变号数有
,∴此处变号数有![]() 个。
个。
综上得 数列![]() 共有
共有![]() 个变号数,即变号数为
个变号数,即变号数为![]() 。
。
解法二:由题设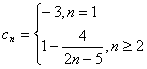 ,
,
![]() 时,令
时,令![]() ;
;
又∵![]() ,∴
,∴![]() 时也有
时也有![]() 。
。
综上得 数列![]() 共有
共有![]() 个变号数,即变号数为
个变号数,即变号数为![]() 。
。