松江区2005学年度第一学期期末质量监控试卷高三数学
一、填空题:
1、 函数![]() 的反函数是
的反函数是 ![]() 。
。
2、 复数![]() 满足
满足![]() ,则
,则![]()
![]() 。
。
3、 已知斜率为![]() 的直线
的直线![]() 与两坐标轴围成面积为
与两坐标轴围成面积为![]() 的三角形,则直线
的三角形,则直线![]() 的方程为
的方程为 ![]() 。
。
4、 不等式![]() 的解集是
的解集是 ![]() 。
。
5、 已知![]() ,点
,点![]() 是角
是角![]() 终边上的点,且
终边上的点,且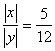 ,则
,则![]()
![]() 。
。
6、 某地自行车的牌照号码由六个数字组成,号码中每个数字可以是![]() 到
到![]() 这十个数字中的任一个。那么某人的一
这十个数字中的任一个。那么某人的一
辆自行车牌照号码中六个数字中![]() 恰好出现两次的概率是
恰好出现两次的概率是 ![]() (精确到
(精确到![]() )。
)。
7、 在![]() 中,
中,![]() ,则
,则![]()
![]() 。
。
8、 已知![]() 、
、![]() 是实系数一元二次方程的两虚根,
是实系数一元二次方程的两虚根,![]() ,且
,且![]() ,则
,则![]() 的取值范围为
的取值范围为 ![]() (用区间表示)。
(用区间表示)。
9、 已知直线![]() 和
和![]() 的夹角为
的夹角为![]() ,那么
,那么![]() 的值为
的值为 ![]() 。
。
 10、对长为
10、对长为![]() 、宽为
、宽为![]() 的一块长方形地面进行绿化,要求四周种花卉,花卉带的宽度相等,中间种草,并且种草的面积不小于总面积的一半,则花卉带的宽度范围为
的一块长方形地面进行绿化,要求四周种花卉,花卉带的宽度相等,中间种草,并且种草的面积不小于总面积的一半,则花卉带的宽度范围为 ![]() (用区间表示)。
(用区间表示)。
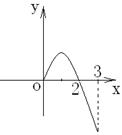
11、如果![]() 是定义在
是定义在![]() 上的奇函数,且当
上的奇函数,且当![]() 时,
时,![]() 的图象
的图象
如图所示。则不等式![]() 的解是
的解是 ![]() 。
。
12、在公差为![]() 的等差数列
的等差数列![]() 中,若
中,若![]() 是
是![]() 的前
的前![]() 项和,则数列
项和,则数列![]() 也成等差数列,且公差为
也成等差数列,且公差为![]() ,类比上述结论,相应地在公比为
,类比上述结论,相应地在公比为![]() 的等比数列
的等比数列![]() 中,若
中,若![]() 是数列
是数列![]() 的前
的前![]() 项积,则有=
项积,则有= ![]() 。
。
二、选择题:
13、若![]() ,
,![]() ,则
,则![]() 等于…………( B )
等于…………( B )
A. ![]() B.
B.
![]() C.
C.
![]() D.
无法计算
D.
无法计算
14、方程![]() 实数解的个数为………… ……………( C )
实数解的个数为………… ……………( C )
A. 0个 B. 1个 C. 2个 D. 3个
15、与函数![]() 的图象相同的函数是………………………………………( D )
的图象相同的函数是………………………………………( D )
A. ![]() B.
B.
![]() C.
C.![]() D.
D. 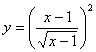
16、设等差数列的前![]() 项和
项和![]() ,
,![]() ,若
,若![]() ,
,![]() ,则使
,则使![]() 成立的最大自然数
成立的最大自然数![]() 为………………………………………………………( C )
为………………………………………………………( C )
A. 2005 B. 2004 C. 4008 D. 4009
三、解答题:
17、已知![]() 为复数,
为复数,![]() 为实数,
为实数,![]() ,且
,且![]() ,求
,求![]() 。
。
解:![]() ,
,![]()
![]() ,∵
,∵![]() ,∴
,∴![]() , ∴
, ∴![]() ,∴
,∴![]() 。
。
18、设![]() ,
,![]()
(1)若![]() ,求
,求![]() 的值;(2)若
的值;(2)若![]() ,求
,求![]() 的值。
的值。
解:(1)![]()
![]() ,
,![]() ,∴
,∴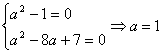 。
。
(2)![]()
![]() ,即
,即![]() ,
,
![]() 时,
时,![]() ;
; ![]() 时,
时,![]() ;
;
![]() 时,
时,![]() ;
; ![]() 时,
时,![]() 。 综上得
。 综上得 ![]() 。
。
19、关于![]() 的方程
的方程![]() 的两根为
的两根为![]() ,且
,且![]() ,若数列
,若数列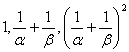 ,
,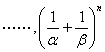 的前100项和为0,求
的前100项和为0,求![]() 的值。
的值。
解: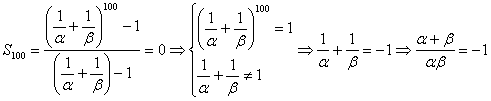 ,
,
∵![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() 。
。
20、某车队2000年初以98万元购进一辆大客车,并投入营运,第一年需支出各种费用12万元,从第二年起每年支出费用均比上一年增加4万元,该车投入营运后每年的票款收入为50万元,设营运![]() 年该车的盈利额为
年该车的盈利额为![]() 元,
元,
(1)写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)从哪一年开始,该汽车开始获利;
(3)若盈利额达最大值时,以20万元的价格处理掉该车,此时共获利多少万元?
解:(1)![]() 。
。
(2)令![]() ,即
,即![]() ,
,
∴从2002年开始,该汽车开始获利。
(3)![]() ,即
,即![]() 时,
时,![]() ,∴此时共获利
,∴此时共获利![]() 万元。
万元。
21、已知等差数列![]() 中,公差
中,公差![]() ,其前
,其前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
,
(1)求数列![]() 的通项公式;
的通项公式;
(2)通过![]() 构造一个新的数列
构造一个新的数列![]() ,是否存在一个非零常数
,是否存在一个非零常数![]() ,使
,使![]() 也为等差数列;
也为等差数列;
(3)求![]() 的最大值。
的最大值。
解:(1)∵等差数列![]() 中,公差
中,公差![]() ,
,
∴ 。
。
(2)![]() ,
,![]()
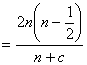 ,令
,令![]() ,即得
,即得![]() ,
,
数列![]() 为等差数列,∴存在一个非零常数
为等差数列,∴存在一个非零常数![]() ,使
,使![]() 也为等差数列。
也为等差数列。
(3)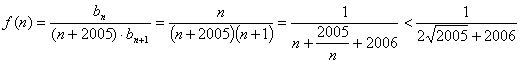 ,
,
∵![]() ,
,
即![]() , ∴
, ∴![]() 时,
时,![]() 有最大值
有最大值![]() 。
。
22、已知函数![]() 是
是![]() 上的奇函数,当
上的奇函数,当![]() 时,
时,![]() ,
,
(1)判断并证明![]() 在
在![]() 上的单调性;
上的单调性;
(2)求![]() 的值域; (3)求不等式
的值域; (3)求不等式![]() 的解集。
的解集。
解:(1)设![]() ,则
,则![]() ,
,![]()
∵![]() ,
,
∴![]() ,即
,即![]() 在
在![]() 上是增函数。
上是增函数。
(2)∵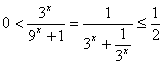 ,∴当
,∴当![]() 时,
时,![]() ;
;
∵当![]() 时,
时,![]()
![]() 。
。
综上得 ![]() 的值域为
的值域为 ![]() 。
。
(3)∵![]() ,又∵
,又∵![]() ,∴
,∴![]() ,此时
,此时![]() 单调递增, ∵
单调递增, ∵![]() ,∴
,∴![]() 时,
时,![]() 。令
。令![]() ,
,
即![]() ,
,
∴不等式![]() 的解集是
的解集是![]() 。
。