江西省重点中学2005-2006第二学期
高三(理科)数学期中试卷
班级
学号 姓名
得分 ![]()
选择题:(每小题3分,共30分)
1![]() 已知
已知![]() ,则
,则![]() 是A
是A![]() B
B![]() C三点构成三角形的 ( )
C三点构成三角形的 ( )
A![]() 充分不必要条件 B
充分不必要条件 B![]() 必要不充分条件
必要不充分条件
C![]() 充要条件 D
充要条件 D![]() 既不充分也不必要条件
既不充分也不必要条件
2![]() 设集合
设集合![]() ,
,![]() ,若
,若![]() ,且(
,且(![]() )
)![]()
![]() =
=![]() ,则实数
,则实数![]() 的取值范围是 ( )
的取值范围是 ( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]() 或
或![]()
3![]() 若函数
若函数![]() 的反函数的图象过
的反函数的图象过![]() 点,则
点,则![]() 点坐标可能是 ( )
点坐标可能是 ( )
A![]() (2,5) B
(2,5) B![]() (1,3) C
(1,3) C![]() (5,2) D
(5,2) D![]() (3,1)
(3,1)
4![]() 已知
已知![]() 是第三象限角,
是第三象限角,![]() 且
且![]() ,则
,则![]() 等于 ( )
等于 ( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
5![]() 若
若![]() ,
,![]() ,则
,则![]() 与
与![]() 的夹角为 ( )
的夹角为 ( )
A![]()
![]() B
B![]()
![]()
C![]()
![]() D
D![]()
![]()
6![]() 已知函数
已知函数![]() 为偶函数,其图象与直线
为偶函数,其图象与直线![]() 的某两个交点横坐标为
的某两个交点横坐标为![]() ,
,![]() 的最小值为
的最小值为![]() ,则 ( )
,则 ( )
A![]()
![]() ,
,![]() B
B![]()
![]() ,
,![]()
C![]()
![]() ,
,![]() D
D![]()
![]() ,
,![]()
7![]() 不等式
不等式![]() 的解集是 ( )
的解集是 ( )
A![]()
![]() B
B![]() [-1,3]
[-1,3]
C![]()
![]() D
D![]()
![]()
8![]() 直线
直线![]() 与曲线
与曲线![]() 有公共点,则
有公共点,则![]() 的取值范围是 ( )
的取值范围是 ( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
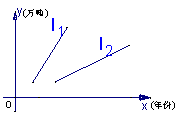
9![]() 对某种产品市场销量情况如图所示,其中:
对某种产品市场销量情况如图所示,其中:![]() 表示产品各年年产量的变化规律;
表示产品各年年产量的变化规律;![]() 表示产品各年的销售情况,下列叙述:
表示产品各年的销售情况,下列叙述:
 ⑴产品产量
⑴产品产量![]() 销售量均以直线上升,仍可按原生产计划进行
销售量均以直线上升,仍可按原生产计划进行
⑵产品已经出现了供大于求的情况,价格将趋跌
⑶产品的库存积压将越来越严重,应压缩产量或扩大销售量
⑷产品的产![]() 销情况均以一定的年增长递增
销情况均以一定的年增长递增
你认为较合理的是( )
A![]() ⑴⑵⑶ B
⑴⑵⑶ B![]() ⑴⑶⑷ C
⑴⑶⑷ C![]() ⑵⑷ D
⑵⑷ D![]() ⑵⑶
⑵⑶
 10
10![]()
![]() 是定义在区间[-c,c]上的奇函数,其图象如图所示:令
是定义在区间[-c,c]上的奇函数,其图象如图所示:令![]() ,则下列关于函数
,则下列关于函数![]() 的叙述正确的是 ( )
的叙述正确的是 ( )
若![]() ,则函数
,则函数![]() 的图象关于原点对称
的图象关于原点对称
B![]() 若
若![]() ,则方程
,则方程![]() 有大于2的实根
有大于2的实根
C![]() 若
若![]() ,则方程
,则方程![]() 有两个实根
有两个实根
D![]()
![]() ,则方程
,则方程![]() 有三个实根
有三个实根
填空题(每小题4分,共16分)
11![]() 若
若![]()
![]()
![]() 满足
满足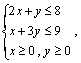 则
则![]() 的最大值为
的最大值为
![]()
12![]() 已知
已知![]() ,
,![]() ,
,![]() 与
与![]() 的夹角为
的夹角为![]() ,要使
,要使![]()
![]()
![]() 与
与![]() 垂直,则
垂直,则![]() =
=
![]()
13![]() 已知
已知![]() ,则
,则![]() 的值是
的值是
![]()
14![]() 若数列
若数列![]() 是等差数列,则有数列
是等差数列,则有数列![]() 也为等差数列,类比上述性质,相应地:若数列
也为等差数列,类比上述性质,相应地:若数列![]() 是等比数列,且
是等比数列,且![]()
![]() 则有
则有![]()
![]() 也是等比数列
也是等比数列![]()
解答题(共6题,54分)
15![]() (本题满分8分)求圆心在直线
(本题满分8分)求圆心在直线![]() ,并且与直线
,并且与直线![]() 相切于点
相切于点![]() 的圆的方程
的圆的方程![]()
16![]() (本题满分8分)已知
(本题满分8分)已知![]() 是定义在
是定义在![]() 上的奇函数,当
上的奇函数,当![]() 时,
时,![]() ,
,
⑴求函数![]() ;⑵解不等式
;⑵解不等式![]()
![]()
17![]() (本题满分8分)已知函数
(本题满分8分)已知函数![]()
![]()
![]() 为 常数,且
为 常数,且![]() )的图象过 点(0,
)的图象过 点(0,![]() ),且函数
),且函数![]() 的最大值为2
的最大值为2![]()
⑴求函数![]() 的解析式,并写出其单调递增区间;
的解析式,并写出其单调递增区间;
⑵若函数![]() 的图象按向量
的图象按向量![]() 作移动距离最小的平移后,使所得图象关于
作移动距离最小的平移后,使所得图象关于![]() 轴对称,求出向量
轴对称,求出向量![]() 的坐标及平移后的图象对应的函数解析式
的坐标及平移后的图象对应的函数解析式![]()
18![]() (本题满分8分)设
(本题满分8分)设![]()
![]()
![]() 是两个不共线的非零向量(
是两个不共线的非零向量(![]() )
)
⑴设![]() ,
,![]() ,
,![]() 那么当实数
那么当实数![]() 为何值时,
为何值时,![]()
![]()
![]()
![]()
![]() 三点共线?
三点共线?
⑵若![]()
![]() 且
且![]() 与
与![]() 夹角为120°,那么实数
夹角为120°,那么实数![]() 为何值时
为何值时![]() 的值最小?
的值最小?
19![]() (本题满分10分)某造纸厂拟建一座平面图形为矩形且面积为200平方米的二级污水处理池(平面图如图所示),池的深度一定,池的外圈周壁建造单价为每米400元,中间一条隔壁建造单价为每米100元,池底建造单价每平方米60元(池壁厚忽略不计)
(本题满分10分)某造纸厂拟建一座平面图形为矩形且面积为200平方米的二级污水处理池(平面图如图所示),池的深度一定,池的外圈周壁建造单价为每米400元,中间一条隔壁建造单价为每米100元,池底建造单价每平方米60元(池壁厚忽略不计)
⑴污水处理池的长设计为多少米时,可使总造价最低;
⑵如果受地形限制,污水处理池的长![]() 宽都不能超过14.5米,那么此时污水处理池的长设计为多少米时,可使总造价最低
宽都不能超过14.5米,那么此时污水处理池的长设计为多少米时,可使总造价最低![]()
20![]() (本题满分12分)已知数列
(本题满分12分)已知数列![]() 满足
满足![]() ,且对一切
,且对一切![]() 有
有![]() ,其中
,其中![]() ,
,
⑴求证对一切![]() 有
有![]() ;
;
⑵求数列![]() 的通项公式;
的通项公式;
⑶求证![]()
![]()
江西省重点中学2005第二学期高三(理科)数学期中试卷
参考答案
1 B 2 B
3 C 4 D
5 C 6 A 7 C 8
D 9 D 10 B 11 7 12 2
13![]()
14 ![]()
15 过点P(3,-2)与切线l 垂直的直线:x-y-5=0与圆心所在的直线4x+y=0的交点(1,-4)即为所求圆的圆心![]() ……4分 又圆半径r=
……4分 又圆半径r=![]() …..5分 所以所求为 (x-1)
…..5分 所以所求为 (x-1)![]() +(y+4) ……6分
+(y+4) ……6分
16 f(x)=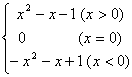 ….4分 x=0显然成立
….4分 x=0显然成立 ![]() 得 0<x<2
得 0<x<2 ![]()
![]() 得 x<-1…7分 综述(-
得 x<-1…7分 综述(-![]() -1)
-1)![]()
![]() …..8分
…..8分
17解:(1)![]()
![]()
所以函数![]() 的解析式是
的解析式是![]() …2分
…2分
![]() 的单调递增区间是
的单调递增区间是![]() …….4分
…….4分
(2)∵平移后的图象对应的函数解析式是![]()
图象关于y轴对称,即![]() 为偶函数,
为偶函数,
![]()
![]() 恒成立
恒成立
![]()
![]() ,
, ![]() ..7分
..7分
故![]()
![]() ,图象对应的函数解析式为
,图象对应的函数解析式为![]() ……..8分
……..8分
18.(1)
![]() ,
,![]()
![]()
![]() 4分
4分
(2)![]() …………..5分
…………..5分
![]()
![]() …………..8分
…………..8分
19Ⅰ()解:设污水处理池的长为x米,则宽为![]() 米
米![]() ………………………1分
………………………1分
总造价![]()
![]() …………………2分
…………………2分
![]()
![]()
=36000(元)………………………………………………………………4分
当且仅当![]() 时,即x=15等号成立
时,即x=15等号成立![]() …………………….6分
…………………….6分
记g(x)=x+![]() ,显然是减函数,……………….8分
,显然是减函数,……………….8分
![]() 有最小值,相应造价f(x)有最小值
有最小值,相应造价f(x)有最小值![]() 此时宽也不超过14.5…….10分
此时宽也不超过14.5…….10分
20 (Ⅰ)由ni=1![]() =Sn2, (1)
由n+1i=1
=Sn2, (1)
由n+1i=1![]() =Sn+12, (2)
=Sn+12, (2)
(2)-(1),得![]() =(Sn+1+Sn)(Sn+1-Sn)=(2 Sn+an+1)
an+1.
=(Sn+1+Sn)(Sn+1-Sn)=(2 Sn+an+1)
an+1.
∵ an+1 >0,∴an+12-![]() =2Sn.
……………………………4分
=2Sn.
……………………………4分
(Ⅱ)由an+12-![]() =2Sn,及an2-an =2Sn-1 (n≥2),
=2Sn,及an2-an =2Sn-1 (n≥2),
两式相减,得(an+1+ an)( an+1-an)= an+1+ an.
∵an+1+ an >0,∴an+1-an =1(n≥2) ……………………………6分
当n=1,2时,易得a1=1,a2=2,∴an+1 - an =1(n≥1).
∴{ an}成等差数列,首项a1=1,公差d=1,故an=n . …………………8分
(Ⅲ)nk=1![]() =nk=1
=nk=1![]() <1+nk=2 ……………………9分
<1+nk=2 ……………………9分
<1+nk=2=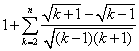
=1+ nk=2 (-) ………………………10分
=1+1+![]() -
-![]() -<2+
-<2+![]() <3.………………………12分
<3.………………………12分