晋江一中、德化一中、国光中学三校
05---06学年高三下学期数学(理科)第二次联考试卷
(考试时间120分钟,满分150分)
一、选择题:(5![]() 12=60)
12=60)
⒈
集合![]() ,
,![]() ,则
,则![]() ( )
( )
A.(0,![]() ) B.(1,
) B.(1,![]() ) C.(
) C.(![]() ,-1) D.(
,-1) D.(![]() ,-1)
,-1)![]() (1,
(1,![]() )
)
2. ![]() 的反函数是 ( )
的反函数是 ( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
3. 若a、b![]() , 则使
, 则使![]() 成立的一个充分不必要条件是( )
成立的一个充分不必要条件是( )
A.![]() B.
B. ![]() 且
且![]() C.
C.![]() D.
D.![]()
4. 过曲线![]() 上一点
上一点![]() 的切线平行于直线
的切线平行于直线![]() ,则点
,则点![]() 的坐标为( )
的坐标为( )
A. (1,4) B.(0,2) C.(-2,0) D.(1,0)
5. 函数![]() 的图象按向量
的图象按向量![]() 平移,使之与
平移,使之与![]() 的图像重合,则
的图像重合,则![]() 可以是( )
可以是( )
A.(![]() ,-1) B. (
,-1) B. (![]() ,1) C. (
,1) C. (![]() ,1) D. (
,1) D. (![]() ,1)
,1)
6. 定义在R上的函数![]() 为奇函数,且
为奇函数,且![]() 若
若![]() 则( )
则( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
7.在△ABC中,![]() 则
则![]() ( )
( )
A . ![]() B.
B. ![]() C.
C. ![]() 或
或![]() D.
D. ![]() 或
或![]()
8. 两个非零向量![]() 、
、![]() 不共线,若
不共线,若![]() ,则实数k的值为( )
,则实数k的值为( )
A. 1
B. -1
C.![]() 1
D. 0
1
D. 0
9. 关于X的不等式![]() 的解集为(1,
的解集为(1,![]() ), 则关于X的不等式
), 则关于X的不等式![]() 的解集( )
的解集( )
A. (-1、2) B. (-∞、-1)∪(2、+∞) C. (1、2) D. (-∞、-2)∪(1、+∞)
10.函数![]() 在定义域
在定义域![]() 内存在反函数且
内存在反函数且![]() 则
则
![]() 为 ( )
为 ( )
A.![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
11. 已知函数![]() ,若
,若![]() 有最小值
有最小值![]() ,则
,则![]() 的最大值为( )
的最大值为( )
A、-1 B、0 C、1 D、2
12.同时具有以下性质:“①最小正周期是π;②图象关于直线![]() 对称;③在
对称;③在![]() 上是增函数”的一个函数是( )
上是增函数”的一个函数是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
二 填空题:(4![]() 4=16)
4=16)
13. 设函数![]() ,
,![]() 若关于X的方程
若关于X的方程![]() 有3个不同的实根,则实数a的取值范围为
有3个不同的实根,则实数a的取值范围为
14. 已知点A(1,-2),若向量![]() 与
与![]() =(2,3)同向,
=(2,3)同向,![]() ,则点B坐标为
,则点B坐标为
15. 已知![]() ,
,![]() ,且
,且![]() 、
、![]() 、
、![]() ,则
,则![]() =
=
16.给出下列四个命题:
①函数![]() 与函数
与函数![]() 的定义域相同;
的定义域相同;
②函数![]() 与
与![]() 的值域相同;
的值域相同;
③函数![]() 与
与![]() 都是奇函数;
都是奇函数;
④函数![]() 与
与![]() 在区间[0,+∞)上都是增函数.
在区间[0,+∞)上都是增函数.
其中正确命题的序号是___________ (把你认为正确的命题序号都填上)
三、解答题:
17.(12分)已知![]() ,且
,且![]() ,
,
求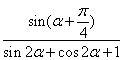 的值.
的值.
18.已知向量![]() ,
,![]()
(1)证明![]()
(2)若存在实数p、 q和非零实数t,使得![]()
![]()
求![]() 的关系式
的关系式
(3)由(2)的结论,写出![]() 的单调递增区间
的单调递增区间
19. 已知:命题![]() 是
是![]() =
=![]() 的反函数且
的反函数且![]() ,命题q:集合
,命题q:集合![]() ,
,![]() 且
且![]() ,求实数a的取值范围,使p、q中有且只有一个为真命题。
,求实数a的取值范围,使p、q中有且只有一个为真命题。
20.(12分)在![]() 中,三内角A、B、C满足条件
中,三内角A、B、C满足条件![]()
(1)判断![]() 形状
形状
(2)若![]() 周长为12,求
周长为12,求![]() 面积的最大值
面积的最大值
21、(12分)某工厂生产一种机器的固定成本为5000元,且每生产100部,需要增加投入2500元,对销售市场进行调查后得知,市场对此产品的需求量为每年500部,已知销售收入的函数为![]()
![]() ,其中
,其中![]() 是产品售出的数量.
是产品售出的数量.
(1)若![]() 为年产量,
为年产量,![]() 表示利润,求
表示利润,求![]() 的表达式;
的表达式;
(2)当年产量为何值时,工厂的利润最大,其最大值是多少?
(3)当年产量为何值时,工厂有盈利?(已知![]() )
)![]()
22.(14分)设关于![]() 的方程
的方程![]() 的两根为
的两根为![]()
![]() ,函数
,函数![]()
(1)求![]() 和
和![]() 的值
的值
(2)证明:![]() 在
在![]() 上是增函数
上是增函数
(3)对任意正数![]() ,求证:
,求证: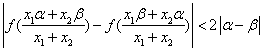
答案
一.1、B 2、D 3、C 4、A 5、B 6、D 7、B 8、C 9、B 10、A 11、C 12、B
二.13、![]() 14、
14、![]() 15、
15、![]() 16、①③
16、①③
三.17、答案:![]() -----------------4
-----------------4
![]()
![]()
![]() ----------------2
----------------2
![]()
![]() ------------2
------------2
原式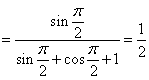 -------------------4 (德一)
-------------------4 (德一)
18、答案:(1)![]() ---------------4
---------------4
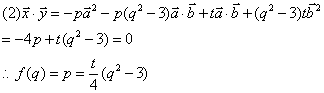 -----------------4
-----------------4
(3)若t>0增区间为(0, +![]() ) t<0 增区间为(-
) t<0 增区间为(-![]() ,0)----------4(晋一)
,0)----------4(晋一)
19、答案:![]() 由
由![]() 得:------------2
得:------------2
![]() ------------------------2
------------------------2
设![]() 判别式为
判别式为![]()
当![]() 时,
时,![]() ,此时
,此时![]() ,
,![]() -------2
-------2
当![]() 时,由
时,由![]() 得
得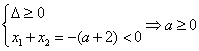 --------2
--------2
![]() a>-4
a>-4
(1)若p真q假![]() --------------------2
--------------------2
(2)若p假q真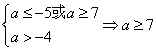 ---------------------2
---------------------2
![]() (晋一)
(晋一)
20、答案:(1)![]() ------------2
------------2
![]()
![]() ------------------------2
------------------------2
![]()
![]() -------------------------2
-------------------------2
![]() ,即
,即![]()
![]()
![]() 为直角三角形--------------------2
为直角三角形--------------------2
(2)![]() -----------------2
-----------------2
![]() -------------------2
(国光)
-------------------2
(国光)
21、答案: (1)
(德一)
22、答案:(1)由题意![]() ,
,![]() ,所以
,所以
![]() ------------2
------------2
同理:![]() ------------------2
------------------2
(2)因![]() ----------------2
----------------2
当![]() 时,
时,![]()
故当![]() 时,
时,![]() ------------------------2
------------------------2
所以,此函数在![]() 上是增函数
上是增函数
(3)
同理:![]() --------------2
--------------2
所以![]() 故
故![]()
又![]()
所以![]()
即![]() ----------------2
----------------2
由(1)得![]() 且
且![]()
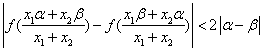 ----------------------2
(国光)
----------------------2
(国光)
![]()
![]()