南昌地区三校联考(一中、十中、新建二中)试卷
数学(文科)
命题学校:新建二中 命题人:李 勇 审题人:徐唐藩
一选择题 : (本大题共12小题,每小题5分,共60分. 每小题只有一项符合题意)
1.已知集合![]() ,则
,则![]() 是 ( )
是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.条件![]()
![]() 是
是![]() 的( )条件
的( )条件
A.充分不必要 B.必要不充分 C.充要 D.既不充分又不必要
3.函数![]() 的图象一个对称中心的坐标是 ( )
的图象一个对称中心的坐标是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.已知数列{an},如果a1,a2-a1,a3-a2,…,an-an-1,…,是首项为1,公比为的等比数列,则an=( )
A.(1-) B.(1-) C.(1-) D.(1-)
5.曲线y=x3-3x2-1在点(1,-3)处的切线方程为 ( )
A. y=3x-7 B. y=-3x C. y=-4x D. y=4x-5
6. 已知函数![]() 的图象过(0,1),则
的图象过(0,1),则![]() 的反函数的图象一定过点 A.(1,2) B.(2,1) C.(0,2) D.(2,0)
的反函数的图象一定过点 A.(1,2) B.(2,1) C.(0,2) D.(2,0)
7. 设![]() ,
,![]() 分别是平面直角坐标系内
分别是平面直角坐标系内![]() 轴、
轴、![]() 轴正方向上的两个单位向量,在同一直线上有A、B、C三个点,
轴正方向上的两个单位向量,在同一直线上有A、B、C三个点,![]() ,若
,若![]() ,则实数
,则实数![]() ,
,![]() 的值分别为( )
的值分别为( )
A. ![]() 或
或![]() B.
B. ![]() 或
或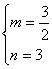
C . ![]() 或
或![]() D.
D. ![]() 或
或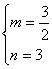
8.二次函数f(x)满足f(3+x)=f(3-x),又f(x)是[0,3]上的增函数,且f(a)≥f(0),那么实数a的取值范围是( )
A. a≥0 B. a≤0 C. 0≤a≤6 D. a≤0或a≥6
9. 设函数f(x) =xsinx,若x1,x2![]() [
[![]() ],且f(x1) < f(x2),则下列结论中必成立的是( )
],且f(x1) < f(x2),则下列结论中必成立的是( )
A. x1 < x2 B. x12 < x22 C. x1 > x2 D. x1+x2 <0
10. 函数y=sin2x+5sin(![]() +x)+3的最小值为( ) A. -3 B. -6 C.
+x)+3的最小值为( ) A. -3 B. -6 C.![]() D. -1
D. -1
11. 设O、A、B、C为平面上四个点,![]() = a,
= a,![]() =b,
=b,![]() =c,且a+b+c=0,
=c,且a+b+c=0,
a·b=b·c=c·a=-1, 则 a+b+c 等于
A. 2![]() B.
2
B.
2![]() C. 3
C. 3![]() D. 3
D. 3![]()
12. 定义运算:![]() ,若数列
,若数列![]() 满足
满足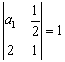 ,且
,且![]() (
(![]() ),则
),则![]() 为( ) A.34 B.36 C.38 D.40
为( ) A.34 B.36 C.38 D.40
二.填空题: (本大题共4小题,每小题4分,共16分)
13.等差数列{an}中,a1=,前n项和为Sn,且S3=S12.则a8= .
14.已知![]() .
.
15.已知函数![]() ,满足
,满足![]()
则![]() .
.
16. 若函数f(x)=![]() x3-
x3-![]() ax2+(a-1)x+1在区间(1,2)内为减函数,在区间(5,+∞)上为增函数,则实数a的取值范围是
.
ax2+(a-1)x+1在区间(1,2)内为减函数,在区间(5,+∞)上为增函数,则实数a的取值范围是
.
三解答题: (本大题共6小题, ,共74分)
17、(本题满分12分)
已知![]() ,
,![]() (
(![]() ),
),
(1)求![]() 关于
关于![]() 的表达式,并求
的表达式,并求![]() 的最小正周期;
的最小正周期;
(2)若![]() ,且
,且![]() 的最小值为5,求
的最小值为5,求![]() 的值.
的值.
18.(本题满分12分)
函数![]() ,以曲线
,以曲线![]() 上的点
上的点![]() 为切点的切线方程为
为切点的切线方程为![]() .
.
(1)若![]() 的表达式;
的表达式;
(2)在(1)的条件下,求![]() 上的最大值.
上的最大值.
19.(本题满分12分)
已知函数f(x)=![]() (x<—
(x<—![]() ),f(x)的反函数为g(x),点An(an,
),f(x)的反函数为g(x),点An(an,![]() )在曲线y=g(x)上(n∈N+),且a1=1.
)在曲线y=g(x)上(n∈N+),且a1=1.
(1)求y=g(x)的表达式;
(2)求数列{an}的通项公式.
20.(本题满分12分)
如图,△AOE和△BOE都是边长为1的等边三角形,
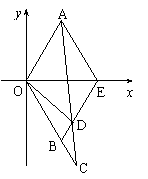 延长OB到C使BC=t(t>0),连AC交BE于D点.
延长OB到C使BC=t(t>0),连AC交BE于D点.
⑴用t表示向量![]() 和
和![]() 的坐标;
的坐标;
⑵当![]() =
=![]() 时,求向量
时,求向量![]() 和
和![]() 的夹角的大小.
的夹角的大小.
21.(本小题满分12分)
设数列![]() 的首项a1=1,前n项和Sn满足关系
的首项a1=1,前n项和Sn满足关系
![]() .
.
(1)求证:数列![]() 是等比数列;
是等比数列;
(2)设数列![]() 的公比是f(t),作数列
的公比是f(t),作数列![]() ,使
,使![]() 求bn;
求bn;
(3)求和:![]()
22.(本小题满分14分)
已知函数:![]()
(1)求f(x)+f(2a-x)的值;
(2)当f(x)的定义域为[a+![]() ,a+1]时,求f(x)的值域;
,a+1]时,求f(x)的值域;
(2)设函数g(x)=x2+(x-a)f(x) ,求g(x) 的最小值 .
2005-2006学年度上学期三校联考高三数学(文)试卷参考解答
一.选择题(本大题12个小题,每小题5分,共60分.每小题只有一项符合要求)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | A | B | A | B | A | C | C | B | D | D | C |
二.填空题(每小题4分,共16分.把答案填在题中横线上)
13. 0 14.![]() 15. 2005 16. [3,6]
15. 2005 16. [3,6]
三.解答题(本大题6个小题,满分74分,解答题应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)
解:(1)![]()
![]()
![]() 的最小正周期是
的最小正周期是![]() ……(6分)
……(6分)
(2)![]() ,
, ![]()
![]()
![]() 的最小值是
的最小值是![]()
![]() ……(12分)
……(12分)
18.(本小题满分12分)

![]()

(2)由(1)知![]()
| x |
| -2 |
|
|
|
|
| + | 0 | - | 0 | + |
|
|
| 极大 |
| 极小 |
|
![]()
![]()
![]() 上最大值为13 ……(12分)
上最大值为13 ……(12分)
19.(本小题满分12分)
解:(1)由y=![]() 得
得![]() ,∴
,∴![]() ∵x<—
∵x<—![]() ,
,
∴![]() ∴g(x)=
∴g(x)= ![]() (x>0) ………………(4分)
(x>0) ………………(4分)
(2)∵点An(an,![]() )在曲线y=g(x)上(n∈N+) ∴
)在曲线y=g(x)上(n∈N+) ∴![]() = g(an)=
= g(an)= ![]() , 并且an >0
, 并且an >0 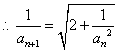 ,
, ![]()
∴数列{![]() }为等差数列。并且首项为
}为等差数列。并且首项为![]() =1,公差为2 ………… (8分)
=1,公差为2 ………… (8分)
∴![]() =1+2(n—1),∴
=1+2(n—1),∴![]() ∵an >0 , ∴
∵an >0 , ∴![]() ……(12分)
……(12分)
20.(本小题满分12分)
⑴![]() =((t+1),-(t+1)),………………………2分
=((t+1),-(t+1)),………………………2分
∵![]() =t
=t![]() ,∴
,∴![]() =t
=t![]() ,
,![]() =
=![]() ,又
,又![]() =(,),
=(,),
![]() =
=![]() -
-![]() =(t,-(t+2));∴
=(t,-(t+2));∴![]() =(,-),…………4分
=(,-),…………4分
∴![]() =(,-) ……………………6分
=(,-) ……………………6分
⑵由![]() =
=![]() 得t=,∴
得t=,∴![]() =(,-),
=(,-),![]() =(-,-)
=(-,-)
∴![]() ·
·![]() =-+= ………………………8分
=-+= ………………………8分
又∵![]() =,
=,![]() == …………………10分
== …………………10分
∴cos<![]() ,
,![]() >==,∴向量
>==,∴向量![]() 与
与![]() 的夹角为60°.………………12分
的夹角为60°.………………12分
21.(本小题满分12分)
解:(1)证明:由已知得![]() 减去
减去
![]() ,化得
,化得![]() .
.
当n=2时,由已知式及a1=1得![]()
数列{an}是以1为首项,![]() 为公比的等比数列. …………(4分)
为公比的等比数列. …………(4分)
(2)解: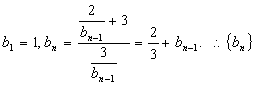 是以1为首项,
是以1为首项,![]() 为公差的
为公差的
等差数列 ![]() ……………
(9分)
……………
(9分)
(3)![]() 当k为奇数时,
当k为奇数时,![]()
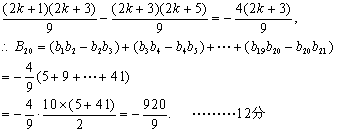
22.(本小题满分14分)
解:(1)![]()
![]() …………………4分
…………………4分
(2)![]()
当![]()
![]() 即
即![]() …………8分
…………8分
(3)解:![]()
①当![]()
如果![]() 即
即![]() 时,则函数在
时,则函数在![]() 上单调递增
上单调递增
![]()
如果![]()
当![]() 时,
时,![]() 最小值不存在 …………………………10分
最小值不存在 …………………………10分
②当![]()
如果![]()
![]()
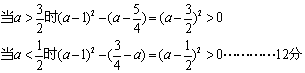
综合得:当![]() 时 g(x)最小值是
时 g(x)最小值是![]()
当![]() 时 g(x)最小值是
时 g(x)最小值是![]()
当![]() 时
g(x)最小值为
时
g(x)最小值为![]()
当![]() 时 g(x)最小值不存在 ………………14分
时 g(x)最小值不存在 ………………14分