南京市第二十七中学
2005届高三(上)数学第一次月考试卷
班级 学号 姓名 得分
一. 选择题(每小题5分,共60分)
1. 设全集U={1, 3, 5, 7, 9},集合A={1, a-5 , 9}, CUA={5, 7}, 则a的值是 ( )
A. 2 B. 8 C. -2或8 D. 2或8
2. 函数![]() 的定义域是
( )
的定义域是
( )
A. ![]() B.
(1,2) C. (2,+∞) D.
(-∞,2)
B.
(1,2) C. (2,+∞) D.
(-∞,2)
3. 若集合![]() 则下列对应中, 不是从P到Q的映射的
则下列对应中, 不是从P到Q的映射的
是 ( )
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
4. 在数列![]() 中,
中, ![]()
![]() 且
且![]() 则
则![]() 为 ( )
为 ( )
A. 5 B. 7 C. 8 D. 10
5. 已知奇函数f (x)是定义域为R, 且以4为周期的周期函数, 又f (1)=4, 那么
f [f ( 7 ) ]等于 ( )
 A. 5
B. 4
C. 0 D. -4
A. 5
B. 4
C. 0 D. -4
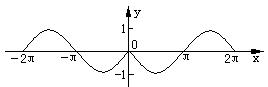
6. 图中的曲线对应的函数是 ( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
7. 在2与7之间插入n个数, 使这个以2为首项的数列成等差数列, 并且S16=56则n=( )
A. 26 B. 25 C. 24 D. 23
8. 记函数![]() 的反函数是
的反函数是![]() 则
则![]() =
( )
=
( )
A. 2 B. -2 C. 3 D. -1
9. 在![]() 内,使
内,使![]() 成立的
成立的![]() 的取值范围是
( )
的取值范围是
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
10. 函数y=![]() 的图象的一条对称轴方程是
( )
的图象的一条对称轴方程是
( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
11. 数列![]() 的前 n项和 S n=
的前 n项和 S n=![]() (n∈N+),当 n≥2时,有
( )
(n∈N+),当 n≥2时,有
( )
A. S n>na1>n a n B. S n<n a n<na1
C. na1<S n<n a n D. n a n<S n<na1
12. 设偶函数![]() 在(0,+∞)上单调递减,则
在(0,+∞)上单调递减,则![]() 与
与![]() 的大小关
的大小关
系是 ( )
A. ![]() =
=![]() B.
B. ![]() >
>![]()
C. ![]() <
<![]() D.
不能确定
D.
不能确定
二. 填空题(每小题4分,共16分)
13. 已知![]() =
=![]() ,则函数f (3 )=
.
,则函数f (3 )=
.
14. 使函数y=f ( x ) 图象上每一点的纵坐标保持不变, 横坐标缩小到原来的![]() ,然后再将
,然后再将
其图象沿x轴向左平移![]() 个单位, 得到的曲线与y=sin2x相同. 则f ( x ) 的表达式为
个单位, 得到的曲线与y=sin2x相同. 则f ( x ) 的表达式为
.
15. 等差数列![]() 中,
中, ![]() , 且
, 且![]() 恰好是某等比数列的前三项, 那么该等比数列
恰好是某等比数列的前三项, 那么该等比数列
的公比等于 .
16. 给出下面四个条件:
① ![]() ②
② ![]() ③
③ ![]() ④
④ ![]()
能使函数![]() 为单调减函数的是
.(填上使命题正确的所有条件的代号)
为单调减函数的是
.(填上使命题正确的所有条件的代号)
三. 解答题(共74分)
17.(本小题满分12分)在△ABC中,
(1) a=7, b=3, c=5, 求最大角和sinC; (2 )
b=(![]() -1)a , C=30°, 求A和B.
-1)a , C=30°, 求A和B.
18.(本小题满分12分)已知R为全集, A=![]() , B=
, B=![]() ,
,
求: CRA![]() B.
B.
 19. ( 本小题满分12分)
在国内投寄外埠平信,每封信不
19. ( 本小题满分12分)
在国内投寄外埠平信,每封信不
超过20克重付邮资80分,超过20克而不超过
40克重付邮资160分.试写出x![]() 克重
克重
的信应付的邮资y (分)与x的函数关系,并求函
数的定义域,然后作出函数的图象.
20.(本小题满分12分)已知等比数列![]() 中,
中, ![]() 前n项的和
前n项的和
![]() 求n和公比q
.
求n和公比q
.
21.(本小题满分12分)已知函数![]() ,
,
(1) 求y=f ( x )的最小正周期;
(2) 当x为何值时, 函数y=f ( x )有最小值, 并求出最小值.
(3) 写出函数y=f (
x )在![]() 上的单调递增区间.
上的单调递增区间.
22.(本小题满分14分)设二次函数![]() , 已知不论α,β为何实数,
, 已知不论α,β为何实数,
恒有f (sinα)≥0和f (2+cosβ)≤0.
(1) 求证:b+c=-1;
(2) 求证:c≥3;
(3) 若函数![]() 的最大值为8, 求b, c的值.
的最大值为8, 求b, c的值.
数 学 参 考 答 案 2004-10-5
一. 选择题(每小题5分,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | B | D | C | C | A | C | B | C | A | D | C |
二. 填空题(每小题4分,共16分)
13. 11 ; 14. ![]() 15. 1
或 4 ; 16. ① ④;
15. 1
或 4 ; 16. ① ④;
三. 解答题(共74分)
17.(本小题满分12分)
解: (1)![]() …………………2分
…………………2分 ![]() …………………3分
…………………3分
![]() …………………4分
…………………4分 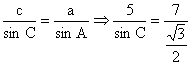 …………………5分
…………………5分
![]() …………………6分
…………………6分
(2)![]() …………………2分
…………………2分
![]() …………………3分
…………………3分
![]() …………………4分
…………………4分
![]() …………………5分
…………………5分
![]() …………………6分
…………………6分
18.(本小题满分12分)
解: 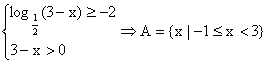 …………………4分
…………………4分
![]() …………………7分
…………………7分
CRA![]() …………………9分
…………………9分
![]() CRA
CRA![]() …………………12分
…………………12分
19.(本小题满分12分)
解: 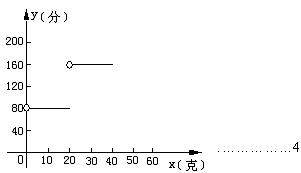
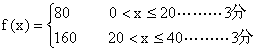
![]()
20.(本小题满分12分)
解: 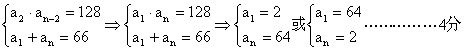
![]() …………………5分
…………………5分
![]() …………………7分
…………………7分
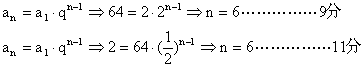
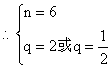 …………………12分
…………………12分
21.(本小题满分12分)
解: (1) ![]() …………………4分
…………………4分
T![]() …………………5分
…………………5分
(2) ![]() …………………7分
…………………7分
此时![]() …………………8分
…………………8分
(3) ![]() ………………10分
………………10分
![]() ①k
①k![]() 时
时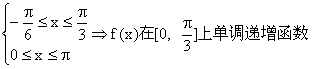 ;
;
![]() ②k
②k![]() 时
时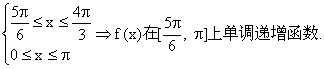 ………………12分
………………12分
22.(本小题满分14分)
解:(1)![]()
![]()
从而知![]() ………………………3分
………………………3分
(2)由![]()
又因为![]() …………………7分
…………………7分
(3)![]() ……………………9分
……………………9分
当![]() …………………………11分
…………………………11分
由![]() 解得
解得![]() …………………………14分
…………………………14分