钦州市大寺中学2006届高三数学(理科)模拟练习(3)
2006.3.16
一.选择题(每小题5分,共60分)
1.若集合![]() ,
,![]() ,则
,则![]() 中元素个数为
中元素个数为
A、1个 B、2个 C、3个 D、4个
2.在下列向量中,与向量a=(1,-![]() 平行的单位向量是t x
平行的单位向量是t x
A.(1,-![]() B.(
B.(![]() ,1)
C.(
,1)
C.(![]() ) D.(-
) D.(-![]() )
)
3.在△ABC中,A<B是cosA>cosB的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.方程![]() 的根所在的区间是
的根所在的区间是
A.(1,2) B.(![]() ,
,![]() ) C.(
) C.(![]() ,
,![]() ) D.(
) D.(![]() ,
,![]() )
)
5.若![]() 的值能被5整除,则
的值能被5整除,则![]() 的可取值的个数有
的可取值的个数有
A、2个 B、3个 C、4个 D、5个
6.下面能得出△ABC为锐角三角形的条件是
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
7.下面四个命题: ①“直线a∥直线b”的充要条件是“a平行于b所在的平面”;
②“直线![]() ⊥平面α内所有直线”的充要条件是“
⊥平面α内所有直线”的充要条件是“![]() ⊥平面
⊥平面![]() ”;
”;
③“直线a、b为异面直线”的充分不必要条件是“直线a、b不相交”;
④“平面α∥平面β”的必要不充分条件是“α内存在不共线三点到β的距离相等”;其中正确命题的序号是
A.①② B.②③ C.③④ D.②④
8.函数y=-sinx+cosx在x∈[-]时的值域是
A. [0,] B.[-,0] C.[0,1] D.[0,]
9.已知定义在实数集上的函数![]() 满足f (x+1)=+2,则f -1(x+1)的表达式是
满足f (x+1)=+2,则f -1(x+1)的表达式是
A.2x-2 B.2x-1 C.2x+2 D.2x+1
10.实数![]() 满足
满足![]() ,则
,则![]() 的值为
的值为
A.8 B.-8 C.8或-8 D.与θ有关
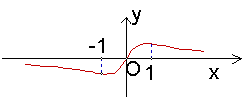 11.若函数
11.若函数![]() 的图象如图,则a的取值范围是
的图象如图,则a的取值范围是
A.(-∞,-1) B.(-1,0)
C.(0,1) D.(1,+∞)
12.双曲线的两个焦点为![]() ,以
,以![]() 为边作等边三角形,若双曲线恰平分三角形的另两边,则双曲线的离心率为
为边作等边三角形,若双曲线恰平分三角形的另两边,则双曲线的离心率为
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
二.填空题(每小题4分,共16分)
13.函数![]() 的最大值是
的最大值是
14.光线从点A(1,1)出发,经y轴反射到圆C:(x-5)2+(y-7)2=4的最短路程等于______
15.过点A(0,-![]() ,则AM的最大值为
,则AM的最大值为![]()
16.直角三角形ABC的斜边AB在平面内![]() ,且平面ABC与
,且平面ABC与![]() 所成的二面角为
所成的二面角为![]() ,若直角边AC与平面
,若直角边AC与平面![]() 成
成![]() 的角,则BC和平面
的角,则BC和平面![]() 所成的角为
所成的角为![]()
三.解答题(第17、18、19、20、21题每题12分,第22题14分,共74分)
17.已知实数![]() 满足不等式
满足不等式![]() ,试判断方程
,试判断方程![]() 有无实根,并给出证明.
有无实根,并给出证明.
18.已知数列![]() 是等比数列,其首项
是等比数列,其首项![]() ,公比为2;数列
,公比为2;数列![]() 是等差数列,其首项
是等差数列,其首项![]() ,公差为
,公差为![]() ,且其前
,且其前![]() 项的和
项的和![]() 满足
满足![]()
(1)求数列![]() 的前
的前![]() 项的和
项的和![]() ;
;
(2)在数列![]() 中任取一项
中任取一项![]() ,在数列
,在数列![]()
![]() 中任取一项
中任取一项![]() ,试求满足
,试求满足![]() 的概率。
的概率。
19.向量![]() ,
,![]() ,
,![]() ,a为常数
,a为常数
(1)求![]() 关于x的函数关系式
关于x的函数关系式![]()
(2)若![]() 时,
时,![]() 的最小值为-2,求a的值
的最小值为-2,求a的值
(3)用五点作图法作出(2)结论中函数在一个周期内的图象。
20.如图,直二面角D-AB-E中,四边形
ABCD是边长为2的正方形,AE=EB,F为
CE上的点,且BF⊥平面ACE。
(1)
 求证:AE⊥平面BCE;
求证:AE⊥平面BCE;
(2) 求二面角B-AC-E的大小;
(3) 求点D到平面ACE的距离。
21.已知函数f(x)是在(0,+![]() )上每一点处可导的函数,若
)上每一点处可导的函数,若![]() 上恒成立,
上恒成立,
(1)求证:函数![]() 上单调递增;
上单调递增;
(2)求证:当![]()
22.在直角坐标系内,△ABC的两个顶点C、A的坐标分别为(-![]() ,三个内角A、B、C满足2sinB=
,三个内角A、B、C满足2sinB=![]()
(1) 求顶点B的轨迹方程;
(1)
过点C做倾斜角为θ的直线与顶点B的轨迹交于P、Q两点,当θ∈(0,![]() 时,求△APQ面积的最大值.
时,求△APQ面积的最大值.
钦州市大寺中学2006届高三数学(理科)模拟练习(3)
答 题 卡
2006.3.16
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 得分 | |||||||||
一、选择题 :用2B铅笔填涂。 (本大题共12小题, 每小题5分, 共60分)
| 1.[ A ] [ B ] [ C ] [ D ] 5. [ A ] [ B ] [ C ] [ D ] 9. [ A ] [ B ] [ C ] [ D ] 2.[ A ] [ B ] [ C ] [ D ] 6. [ A ] [ B ] [ C ] [ D ] 10. [ A ] [ B ] [ C ] [ D ] 3.[ A ] [ B ] [ C ] [ D ] 7. [ A ] [ B ] [ C ] [ D ] 11. [ A ] [ B ] [ C ] [ D ] 4.[ A ] [ B ] [ C ] [ D ] 8. [ A ] [ B ] [ C ] [ D ] 12. [ A ] [ B ] [ C ] [ D ] |
二、填空题:(本大题共4小题,每小题4分,共16分.把答案填在题中横线上)
| 13 14 15 16 |
三、解答题(本大题共6个小题,共74分,解答应写出文字说明,证明过程或演算步骤)
| 17、(本小题满分12分) |
| 18.(本题满分12分) |
| 19.(本题满分13分) |
|
|
| 21.(本题满分12分) |
| (接21题) |
| 22.(本题满分13分) |
钦州市大寺中学2006届高三数学(理科)模拟练习(3)
参考答案
一.选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | D | C | B | D | D | D | D | B | A | D | A |
二.填空题
13.1;14.6![]() -2;15.
-2;15.![]() ;16.
;16.![]() 。
。
三.解答题
17.解:(1)![]() 等价于
等价于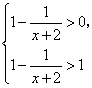 …………………………3’
…………………………3’
解得![]() .…………6’
.…………6’
(2)方程![]() 的判别式
的判别式![]() .…………8’
.…………8’
∵ ![]() ,∴
,∴![]() .即
.即![]() .…………………………………………10’
.…………………………………………10’
∴ ![]() .
.
由此得方程![]() 无实根.………………………………………12’
无实根.………………………………………12’
18.(1)解:由题意得:![]() ,由
,由![]() ,得
,得![]() ……………4’
……………4’
![]() …………………………………………………6’
…………………………………………………6’
(2)解:![]() ,为1,2,4,8;
,为1,2,4,8;![]() ,为1,4,7,10
,为1,4,7,10
有序实数对![]() 共有16个,……………………………………………………………………8’
共有16个,……………………………………………………………………8’
当![]() 时,
时,![]() 取1,4,7共3个;当
取1,4,7共3个;当![]() 时,
时,![]() 取1,4,7共3个
取1,4,7共3个
当![]() 时,
时,![]() 取1,4,7共3个;当
取1,4,7共3个;当![]() 时,
时,![]() 取1,4共2个;……………………10’
取1,4共2个;……………………10’
满足题意的点共11个,所求的概率为![]() ………………………………………………………12’
………………………………………………………12’
19.解:(1)![]()
![]()
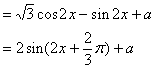 …………………………………………4’
…………………………………………4’
(2)![]() ,
,![]()
![]()
![]() …………………………………………………………………8’
…………………………………………………………………8’
(3)………………………………………………………………………………………13’
20.解法一:(1) ∵BF⊥平面ACE![]() BF⊥AE
BF⊥AE
又二面角D-AB-E为直二面角且CB⊥AB ![]() CB⊥平面ABE
CB⊥平面ABE ![]() CB⊥AE
CB⊥AE
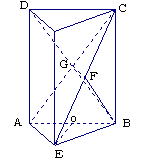 ∴AE⊥平面BCF即AE⊥平面BCE
……………………2分
∴AE⊥平面BCF即AE⊥平面BCE
……………………2分
(2) 连结BD交AC于G,连结FG。由ABCD
是边长是2的正方形有:BG⊥AC且BG=![]() ;
;
又BF⊥平面ACE。所以由三垂线定理得:FG⊥AC,
于是∠BGF是二面角B-AC-E的平面角。………………4分
又由①知:AE⊥平面BCE ![]() AE⊥BE
AE⊥BE
∴由AE=BE知AEB是等腰直角三角形,BE=![]()
又在直角三角形BCE中,![]() ,
,![]()
∴直角三角形BFG中,sin∠BGF=![]() ……………………6分
……………………6分
故二面角B-AC-E的大小为![]() .
……………………7分
.
……………………7分
(3) 过E作EO⊥AB交AB于O点,OE=1。由二面角D-AB-E为直二面角知:EO⊥平面ABCD。 ……………………9分
设D到平面ACE的距离为h,由![]()
![]()
![]() ……………………11分
……………………11分
∴点D到平面ACE的距离为![]() 。
……………………12分
。
……………………12分
解法二:(1)同解法一。 ……………………2分
(2) 如图,以线段AB的中点为原点为O,OE所在直线为x轴,AB所在直线为y轴,过O点平行于AD的直线为z轴,建立空间直角坐标系。 ……………………4分
由AE⊥平面BCE有AE⊥BE。在Rt△AEB中,AB=2,O为AB的中点,则OE=1,A(0,-1,0)、E(1,0,0)、C(0,1,2)。![]() ,
,![]() . ……………………5分
. ……………………5分
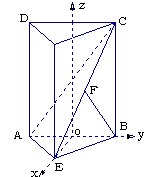 设平面AEC的一个法向量为n=(x,y,z),
设平面AEC的一个法向量为n=(x,y,z),
则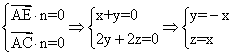 ,
,
从而平面AEC的一个法向量为n=(1,-1,1)…………7分
又平面ABC的一个法向量为m=(1,0,0).
∴cos〈m,n〉= ![]() ……………………9分
……………………9分
故二面角B-AC-E的大小为![]() . ……………………10分
. ……………………10分
(3)∵AD//z轴且AD=2 ![]()
![]()
∴点D到平面ACE的距离d=![]() cos〈
cos〈![]() ,n〉=
,n〉= ![]() …………………12分
…………………12分
21.(1)证明:由g(x)=![]() ′(x)=
′(x)=![]()
由xf′(x)>f(x)可知:g′(x) >0在x>0上恒成立.
从而g(x)=![]() …………………………………… 5分
…………………………………… 5分
(2)由(1)知g(x)=![]()
在x1>0,x2>0时,![]()
![]() ……………………9分
……………………9分
于是f(x1)<![]() ………………………11分
………………………11分
两式相加得到:f(x1)+f(x2)<f(x1+x2) ………………………………………………12分
22.解:
(1)因为2sinB=![]() ,根据正弦定理得2b=
,根据正弦定理得2b=![]()
又b=2![]() ,所以a+c=4由椭圆定义知顶点B的轨迹为椭圆,其方程为
,所以a+c=4由椭圆定义知顶点B的轨迹为椭圆,其方程为![]() 4’
4’
设PQ方程为y=tanθ(x+![]() ),θ∈(0,
),θ∈(0,![]()
由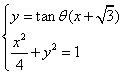 得(1+4tan2θ)x2+8
得(1+4tan2θ)x2+8![]() xtan2θ+12tan2θ-4=0 ……………………6’
xtan2θ+12tan2θ-4=0 ……………………6’
设P(x1,y1),Q(x2,y2),则x1+x2=![]() ……………………8’
……………………8’
又PQ=![]() 点A到PQ的距离d=
点A到PQ的距离d=![]() ,θ∈(0,
,θ∈(0,![]() ……………………10’
……………………10’
S△ABC=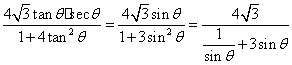 ≤2…………………………………12’
≤2…………………………………12’
当且仅当![]() △APQ的最大面积为2. …………13’
△APQ的最大面积为2. …………13’