第一学期期末高三数学文史类

青岛15中2005-2006学年度第一学期期末

高　 三　 数　学　文史类

本试卷分第Ⅰ卷(选择题　共60分)和第Ⅱ卷(非选择题　共90分)，考试时间为120分钟，满分为150分.

第Ⅰ卷　(选择题　共60分)

参考公式：

如果事件A、B互斥，那么P(A+B)=P(A)+P(B)

如果事件A、B相互独立，那么P(A·B)=P(A)·P(B)

如果事件A在试验中发生的概率是p，那么n次独立重复试验中恰好发生k次的概率P_n(k)=Cp^k(1－p)^n-k

正棱锥、圆锥的侧面积公式S_锥侧=cl，

其中c表示底面周长，l表示斜高或母线长

球的表面积公式S=4πR²，其中R表示球的半径

球的体积公式V=πR³，其中R表示球的半径

一、选择题(本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)

1.已知A={xx+1≥0}，B={yy²－2>0}，全集I=R，则A∩_IB为

A.{xx≥或x≤－}　　　　　　　　　　　　　　　　　B.{xx≥－1或x≤}

C.{x－1≤x≤}　　　　　　　　　　　　　　　　　　 D.{x－≤x≤－1}

2.不等式log (x－1)>－1的解集为

A.{xx>4}　　　　　　　　　　　　　　　　　　　　　　　　　　　B.{xx<4}　

C.{x1<x<4}　　　　　　　　　　　　　　　　　　　　　　　　　 D.{x1<x<}

3.下列函数中，图象与函数y=4^x的图象关于y轴对称的是

A.y=－4^xB.y=4^-xC.y=－4^-x D.y=4^x+4^-x

4.在以下关于向量的命题中，不正确的是

A.若向量a=(x，y)，向量b=(－y，x)(x、y≠0)，则a⊥b

B.四边形ABCD是菱形的充要条件是=，且=

C.点G是△ABC的重心，则++=0

D.△ABC中，和的夹角等于180°－A

5.已知函数y=x³－3x，则它的单调增区间是

A.(－∞，0)　　　　　　　　　　　　　　　　　　　　　　　　　　 B.(0，+∞)

C.(－1，1)　　　　　　　　　　　　　　　　　　　　　　　　　　　D.(－∞，－1)及(1，+∞)

6.已知数列{a_n}是各项均为正数的等比数列，公比q≠1，那么

A.a₃²+a₇²>a₄²+a₆²B.a₃²+a₇²<a₄²+a₆²

C.a₃²+a₇²=a₄²+a₆²D.大小不确定

7.曲线y=x³+x－2的一条切线平行于直线y=4x－1，则切点P₀的坐标为

A.(0，－2)或(1，0)　　　　　　　　　　　　　　　　　　　　 B.(1，0)或(－1，－4)

C.(－1，－4)或(0，－2)　　　　　　　　　　　　　　　　　D.(1，0)或(2，8)

8.函数y=f(x+1)与y=f(1－x)的图象关于

A.y轴对称　　　　　　　　　　　　　　　　　　　　　　　　　　　B.原点对称

C.直线x=1对称　　　　　　　　　　　　　　　　　　　　　　　D.关于y轴对称且关于直线x=1对称

9_.已知(－ax+b)=2，则b的值为

A.0　　　　　　　　　　　　　　　B.4　　　　　　　　　　　　　　　C.－4　　　　　　　　　　　　　 D.不确定

10.设f(x)、g(x)在［a，b］上可导，且f′(x)＞g′(x)，则当a＜x＜b时，有

A.f(x)＞g(x)　　　　　　　　　　　　　　　　　　　　　　　　　　B.f(x)＜g(x)

C.f(x)+g(a)＞g(x)+f(a)　　　　　　　　　　　　　　　　　　 D.f(x)+g(b)＞g(x)+f(b)

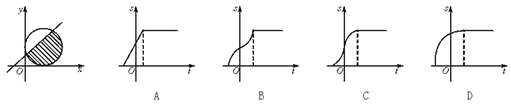
11.如图，圆C：(x－1)²+(y－1)²=1在直线l:y=x+t下方的弓形(阴影部分)的面积为S，当直线l由下而上移动时，面积S关于t的函数图象大致为

12.函数f(x)=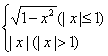，如果方程f(x)=a有且只有一个实根，那么a满足

A.a<0　　　　　　　　　　　　　B.0≤a<1　　　　　　　　　　　 C.a=1　　　　　　　　　　　　　D.a>1

第Ⅱ卷　(非选择题　共90分)

二、填空题(本大题共4小题，每小题4分，共16分，把答案填在题中横线上)

13.北京市某中学要把9台型号相同的电脑送给西部地区的三所希望学校，每所小学至少得到2台，不同送法的种数共有__________种.

14.已知f(x)=log₃x，当0<a<2时，有f(a)>f(2)，则a的取值范围是__________.

15.已知无穷等比数列首项为2，公比为负数，各项和为S，则S的取值范围为__________.

16.设有四个条件：

①平面γ与平面α、β所成的锐二面角相等；

②直线a∥b，a⊥平面α，b⊥平面β；

③a、b是异面直线，aα，bβ，且a∥β，b∥α；

④平面α内距离为d的两条直线在平面β内的射影仍为两条距离为d的平行线.

其中能推出α∥β的条件有__________.(填写所有正确条件的代号)

三、解答题(本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤)

17.(本小题满分12分)

△ABC中，a、b、c分别是∠A、∠B、∠C的对边.已知tanA+tanB+=tanA·tanB·，

(1)求∠C的大小；

(2)若c=，△ABC的面积S_△ABC=，求a+b的值.

18.(本小题满分12分)

已知a，b都是非零向量，且a+3b与7a－5b垂直，a－4b与7a－2b垂直，求a与b的夹角.

19_.(本小题满分12分)

已知曲线C：x²－y²=1及直线L：y=kx－1.

(1)若L与C有两个不同的交点，求实数k的取值范围；

(2)若L与C交于A、B两点，O是坐标原点，且△OAB的面积为，求实数k的值.

20.(本小题满分12分)

如图，已知三棱锥P—ABC中，PA⊥平面ABC，PA=3，AC=4，PB=PC=BC.

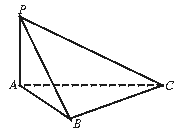
(1)求三棱锥P—ABC的体积V；

(2)作出点A到平面PBC的垂线段AE，并求AE的长；

(3)求二面角A—PC—B的大小.

21.(本小题满分12分)

某水库水位已超过警戒水位(设超过的水量为P)，由于上游仍在降暴雨，每小时将流入水库相同的水量Q，为了保护大坝的安全，要求水库迅速下降到警戒水位以下，需打开若干孔泄洪闸(每孔泄洪闸泄洪量都相同).要使水位下降到警戒水位，经测算，打开两孔泄洪闸，需40小时；打开4孔泄洪闸，需16小时.现要求在8小时内使水位下降到警戒水位以下，问：至少需打开几孔泄洪闸？

22.(本小题满分14分)

函数f(x)=log_a(x－3a)(a>0且a≠1)，当点P(x，y)是函数y=f(x)图象上的点时，Q(x－2a，－y)是函数y=g(x)图象上的点.

(1)写出函数y=g(x)的解析式；

(2)当x∈［a+2，a+3］时，恒有f(x)－g(x)≤1，试确定a的取值范围.

参　考　答　案

仿真试题(一)

一、选择题(每小题5分，共60分)

1.解析：由已知得A={xx≥－1}，B={yy＞或y＜－，_IB={y－≤y≤}，则A∩_IB={x－1≤x≤}，选C.

答案：C

2.解析：由已知得得1＜x＜4，选C.

答案：C

3.解析：关于y轴对称的规律是以－x代x，y代y，得所求函数为y=4^-x，选B.

答案：B

4.解析：若点G是△ABC的重心，则有++=0，而C的结论是++=0，显然是不成立的，选C.

答案：C

5.解析：由y=x³－3x，得y′=3x²－3.令y′=0，得x=±1.列表:

y	(－∞，－1)	(－1，1)	(1，+∞)
y′	＞0	＜0	＞0

所以函数y=x³－3x的单调增区间为(－∞，－1)及(1，+∞)，选D.

答案：D

6.解析：取特殊数列验证：

根据题意取数列1，2，4，8，16，32，64(q＞1)，易证a₃²+a₇²>a₄²+a₆²；取数列64，32，16，8，4，2，1(0＜q＜1)，易证a₃²+a₇²>a₄²+a₆²，故选A.

答案：A

7.解析：由y=x³+x－2，得y′=3x²+1，由已知得3x²+1=4，解之得x=±1.当x=1时，y=0;当x=－1时，y=－4.

∴切点P₀的坐标为(1，0)或(－1，－4)，选B.

答案：B

8.解析：根据对称关系验证D正确，选D.

答案：D

9_.解析：－ax+b

=

=.

∵(－ax+b)=2，

得得选B.

答案：B

10.解析：令F(x)=f(x)－g(x)，x∈［a，b］，

则F′(x)=f′(x)－g′(x)＞0.∴F(x)在［a，b］上是增函数.

又a＜x＜b，得F(a)＜F(x)＜F(b)，

即f(a)－g(a)＜f(x)－g(x)＜f(b)－g(b).

得f(x)+g(a)＞g(x)+f(a)，选C.

答案：C

11.解析：当t=－时，S=0;当t≥时，S=π;

当t=0时，S=.对照图象知B符合题意，故选B.

答案：B

12.解析：由图知a=1时，图象只有一个交点，故选C.

答案：C

二、填空题(每小题4分，共16分)

13.解析：分为三种情况：①每所学校得3台电脑；②有两所学校各得2台电脑，一所学校得5台电脑；③有一所学校得2台电脑，一所学校得3台电脑，一所学校得4台电脑.

答案：10

14.解析：由f(a)＞f(2)，得log₃a＞log₃2.

log₃a＞log₃2或log₃a＜－log₃2=log，

得a＞2或0＜a＜，又0＜a＜2，

∴0＜a＜.

答案：0＜a＜

15.解析：由已知S=，得q=.又－1＜q＜0得－1＜＜0.解之得1＜S＜2.

答案：1＜S＜2

16.解析：

①　　　　　　　不正确

②　　　　　　　正确

③　　　　　　　正确

④　　　　　　　不正确

故②③正确.

答案：②③

三、解答题(17、18、19、20、21题每题12分，22题14分，共74分)

17.解：(1)tanC=－tan(A+B)

=－

=－

=.

∵0°＜C＜180°，∴C=60°.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 6分

(2)由c=及余弦定理，

得a²+b²－2abcos60°

=()².

又由S_△ABC=absin60°=，

整理得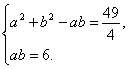

∴(a+b)²=，即a+b=.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 12分

18.解：∵a+3b与7a－5b垂直，a－4b与7a－2b垂直，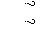

∴(a+3b)·(7a－5b)=0，(a－4b)·(7a－2b)

=0.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 4分

即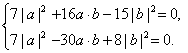　　　　　　 

两式相减：a·b=b²，代入①得a²=b².　　　　　　　　　　　　　　　　　　　　　　　　　　　　 8分

∴cosα==.∴α=60°，即a与b的夹角为60°.　　　　　　　　　　　　　　　　　 12分

19_.解：(1)曲线C与直线L有两个不同交点，则方程组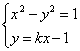有两个不同的解.

代入整理得：(1－k²)x²+2kx－2=0.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 2分

此方程必有两个不等的实根x₁，x₂，

∴

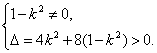
解得－＜k＜且k≠±1时，曲线C与直线L有两个不同的交点.　　　　　　　　　　 6分

(2)设交点A(x₁，y₁)，B(x₂，y₂)，直线L与y轴交于点D(0，－1)，

∴

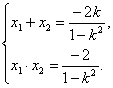
∵S_△OAB=S_△OAD+S_△OBD

=x₁+x₂

=(x₁+x₂)　 (∵x₁·x₂＜0　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 8分

=x₁－x₂=，

∴(x₁－x₂)²=(2)²，即()²+=8.解得k=0或k=±.

∵－＜k＜，

∴k=0或k=±时，△OAB面积为.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 12分

20.解：(1)∵PA⊥平面ABC，PB=PC，由射影定理得，AB=AC=4.

∵PA⊥平面ABC，∴PA⊥AC.

在Rt△PAC中，可求出PC=5，则PB=BC=5.

取BC中点D，连AD.在等腰△ABC中，求出底边上的高AD=.

∴V=··5··3=.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　4分

(2)连PD，则PD⊥BC，又AD⊥BC，

∴BC⊥平面PAD.又BC平面PBC，∴平面PAD⊥平面PBC.

作AE⊥PD于E，则AE⊥平面PBC，AE为点A到平面PBC的垂线段.

在Rt △PAD中，由PA·AD=AE·PD，即3·=AE·，求出AE=.8分

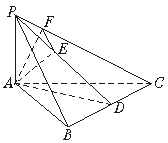
(3)作AF⊥PC于F，连EF，由三垂线逆定理，得EF⊥PC.

∠AFE为二面角A—PC—B的平面角.

在Rt△PAC中，由PA·AC=PC·AF，即3·4=5·AF，求出AF=，

∴sinAFE==·=.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　 12分

即二面角A—PC—B为arcsin.

21.解：设应打开n孔泄洪闸，每孔泄洪闸每小时的泄洪量为R，则有

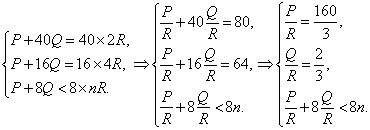　　　　　　　　　　　　　　　　　7分

∴8n＞.从而n＞≈7.3.

答：至少要打开8孔泄洪闸.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 12分

22.解：(1)设P(x₀，y₀)是y=f(x)图象上的点，Q(x，y)是y=g(x)图象上的点，则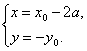

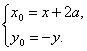∴∴－y=log_a(x+2a－3a).

∴y=log_a(x＞a)，即y=g(x)=log_a(x＞a).　　　　　　　　　　　　　　　　　　　　　　　　　5分

(2)∵　∴x＞3a.

∵f(x)与g(x)在［a+2，a+3］上有意义，∴3a＜a+2.∴0＜a＜1.　　　　　　　　　　　　　　　 8分

∵f(x)－g(x)≤1恒成立，∴log_a(x－3a)(x－a)≤1恒成立.

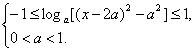
∴a≤(x－2a)²－a²≤.

对x∈［a+2，a+3］时恒成立，令h(x)=(x－2a)²－a²，其对称轴x=2a，2a＜2，2＜a+2，

10分

∴当x∈［a+2，a+3］时，h(x)_min=h(a+2)，h(x)_max=h(a+3).

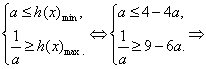∴0＜a≤.　　　　　　　　　　　　　　　　　　　　　 14分