江苏省灌云县2005届高三第一次八校联考

数学测试卷（文）04.10.3

　　　　 　　　　　 　 第I卷　　　　  命题人：孙广军　翟洪亮  李红艳

一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中,只有一个是符合题目要求的. 请将答案填在第II卷的相应处。

1.已知等于　（　 ）

A．　 B．　C．　　　　D．R

2.设p、q为简单命题，则“p且q”为假是“p或q”为假的　　　　　　 （　　）

　　A．充分不必要条件　　　　　　　　　 B．必要不充分条件

　　C．充要条件　　　　　　　　　　　　 D．既不充分也不必要条件

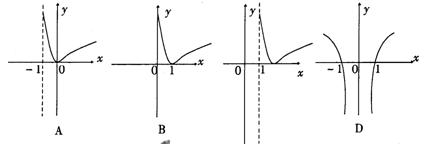
3.函数y= lg（x-1） 的图象是（　　 ）

C

4. 已知等差数列的前项和为 ,若,则等于　　　　　　 （　　）

A．72　　　 B．54　　　 C．36　　　 D．18

 5. 设集合，则集合的子集的个数是　　 　　　　　　　　　　　（　　）

　　A．11　　　　　　 B．10　　　　　　 C．15　　　　　　 D．16

6.若函数（>0且）的图象过点(0，1)和（，0），则的值为　　　　　　　　　　　　　　　　　　　　　　　 （　 ）　　　　  　　　　　　　　　　　　　　　　　　　　　　　　　　 

A．4　　  B．　　  C．3　　　 D．

7.若不等式＞在上有解,则的取值范围是　　　　（　　）

　 A． 　　　B. 　　　C．　 　　　　　D．

8. 若等差数列{a_n}中，a₂+a₆+a₁₆为一个确定的常数，则其前n项和S_n中也为确定的常数的是　　　　　　　　（　　）

　　A．S₁₇ B．S₁₅ C．S₈D．S₇

9.已知集合A={x}，B={x3<x<5},则能使AB成立的实数的取值范围是　　　　　　　　　　　　　　　　　　　　　　　　　　  （　　 ）

　 A.{3<4}　　　B. {34} 　　　C. {3<<4} 　　 D. φ

10. 若函数的定义域为[-1，1],则函数的定义域为　　　　  （　　）

A. [-1，1]　　　　B. （0，1）　　　　C.（0，2）　　　　  D. [1，2]

11. 已知是偶函数，则函数的图象的对称轴是　 （　　）

A．　　B．　　 C． 　 D． 　 

12. 设奇函数上是增函数，且若函数对所有的都成立，当时，则t的取值范围是　　　　　 （　　）

　　A．　　　　　　　　　　　 B．　　

　　C．　　　　　　　D．

二、填空题：本大题共4小题，每小题4分，共16分.请将答案填在第II卷的相应处。

13. 在等差数列｛a_n｝中，a₁=,第10项开始比1大，则公差d的取值范围是___________.

14.已知函数f(x)满足：f(p+q)=f(p)f(q),f(1)=3,则

=　　　　　   ．　

15. 在等比数列｛a_n｝中, ,,则　　　　　　　　 .

16.如右图，它满足：（1）第n行首尾两数均为n，

（2）表中的递推关系类似杨辉三角，则第n行

（n≥2）第2个数是　　　　   .

灌云县2005届高三第一次联考

数学测试卷（文）04.10.3

　　　　　　　　　　　 第II卷 　　　　 命题人：孙广军　翟洪亮  李红艳

一、选择题：（5分×12=60分）

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案

二、填空题（4分×4=16分）

13、　　　　　  14、　　　　　　 15、　　　　　　 16、　　　　　 

三、解答题：(本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤．)

17.(本题满分12分)已知数列｛a_n｝中,是其前项的和,且对不小于2的正整数满足关系.

（I）求、、；

（II）求数列｛a_n｝的通项.

18. (本题满分12分) 设函数（、）

(I)若，且对任意实数x均有0成立，求实数、的值.

(II)在(I)的条件下，当[－2，2]时，是单调函数，求实数的取值范围.

19. (本题满分12分) 某渔业公司年初用128万元购买一艘捕鱼船，第一年各种费用12万元，以后每年都增加4万元，每年捕鱼收益50万元。

　　（I）问第几年开始获利？

　　（II）若干年后，有两种处理方案：

　　（1）年平均获利最大时，以26万元出售该渔船；

　　（2）总纯收入获利最大时，以8万元出售该渔船。

问哪种方案合算？

20. (本题满分12分)已知等差数列｛｝的前n项的和为，=5，=155.(I)求数列｛｝的通项公式；（II）若从数列｛｝中依次取出第2，4，8，…，，…项，按原来的顺序排成一个新数列｛｝，试求｛｝的前n项的和.

21. (本题满分12分)已知， （>2）.（I）求、同时有意义的实数x的取值范围；

（II）求=+的值域.

22. (本题满分14分)已知函数是定义在R上的偶函数.当X0时, =.

(I)　　　　　　  求当X<0时, 的解析式;

(II)　　　　  试确定函数= (X0)在的单调性，并证明你的结论.

(III)　　　 若且，证明：－<2.

参考答案

江苏省灌云县2005届高三第一次八校联考数学测试卷（文）04.10.3

一、选择题：（5分×12=60分）

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案	A	B	C	A	D	A	C	B	B	D	C	C

二、填空题（4分×4=16分）

13、14、　　　 24　　　15、 或16、

17、（I）、、；

（II）数列｛a_n｝的通项.

18、(I) =1、=2.

(II)实数的取值范围是或.

19、（I）第五年　 ;

　　　（II）第(1)方案乘余90万元,第(2)方案乘余80万元,故第(1)方案合算

20、(I)数列｛｝的通项公式=；（II），前n项的和=.

21、（I）、同时有意义的实数x的取值范围；

（II）=+的值域为（1）当时，的值域为；（2）当时，的值域为.

22、（1）当X<0时,

（2）函数= (X0)在是增函数；

（3）因为函数= (X0)在是增函数，由得，又因为，所以，所以，因为，所以，且，即，所以，即－<2.