江苏省海安高级中学高三年级第一次统测
数 学 试 卷 第I卷（选择题，共60分）
一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合要求的.）
1．定义 
.若
，
则
A.{4，8} B.{1，2，6，10} C.{1} D.{2，6，10}
2．等差数列
中，若
，
，则前9项的和
等于
A．66 B．99 C．144 D．297
3．若0＜a＜1，且函数
，则下列各式中成立的是
A．
B．
C．
D．
4．函数
的反函数图像是
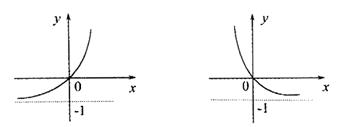
A B
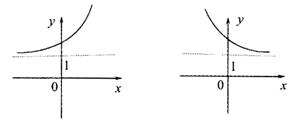
C D
5．今有命题p、q，若命题S为“p且q”，则“
或
”是“
”的
A．充分而不必要条件 B．必要而不充分条件
C．充要条件 D．既不充分也不必要条件
6．成等差数列的3个正数的和等于15，并且这三个数分别加上1，3，9后又成等比数列.
那么这三个数的乘积等于
A．210 B .105
C．70 D. 35
7．已知数列前n项和为
，则
的值是
A．13 B．-76 C．46 D．76
8．函数
与
图像关于直线x-y＝0对称，则
的单调增区间是
A．（0，2） B．（-2，0） C．（0，＋∞） D．（-∞，0）
9．已知函数
满足
且
∈[-1，1]时，
，则方程
解的个数是：
A．4 B. 6 C.8 D. 10
10．已知数列的前n项和为
，
，现从前m项：
，
，…，
中抽出一项（不是，也不是），余下各项的算术平均数为37，则抽出的是
A．第6项 B．第8项 C．第12项 D．第15项
11．将正奇数按下表排成5列
|
| 第1列 | 第2列 | 第3列 | 第4列 | 第5列 |
| 第1行 |
| 1 | 3 | 5 | 7 |
| 第2行 | 15 | 13 | 11 | 9 |
|
| 第3行 |
| 17 | 19 | 21 | 23 |
| …… |
| …… | 27 | 25 |
|
那么2005应该在第 行，第 列.
A．250，3 B．250，4
C．251，4 D．251，5
12．某种细菌
在细菌
的作用下完成培养过程，假设一个细菌与一个细菌可繁殖为2个细菌与0个细菌,今有1个细菌和512个细菌,则细菌最多可繁殖的个数为
A．511 B.512 C.513 D.514
第Ⅱ卷（非选择题，共90分）
二、填空题（本大题共4小题，每小题4分，共16分）
13．等差数列
中，
，公差
，则
的值等于___________________.
14. 已知二次函数f（x）= x2－3x + p－1，若在区间[0，1]内至少存在一个实数c，
使f（c）＞0，则实数p的取值范围是_____________.
15. 若数列，
是等差数列，则有数列
也为等差数列，类比上述性质，相应地：若数列
是等比数列，且
，则有
______ 也是等比数列．
16．已知函数
.给出下列命题：①f(x)必是偶函数；②f(0)= f(2)时，f(x)的图象必关于直线x=1对称；③若
，则f(x)在区间
上是增函数；
④f(x)有最小值
.
其中正确命题的序号是 .
三、解答题（本大题共6小题，共74分，解答应写出文字说明，证明过程，或演算步骤）
17．（本小题满分12分）
已知函数
.
（I）函数
和
是否具有奇偶性，并说明理由；
（II）证明函数在
上为增函数。
18．（本小题满分12分
命题p:函数
的定义域为
；命题q:不等式
对一切正实数均成立.如果命题p或q为真命题，命题p且q为假命题，求实数a的取值范围.
19．（本小题满分12分）
无穷数列的前n项和
，并且≠．
（1）求p的值；
（2）作函数
，如果
，
20.（本小题满分12分）
某工厂统计资料显示，产品次品率p与日产量n (件)
的关系表如下：
| n | 1 | 2 | 3 | 4 | ┅ | 98 |
| p |
|
|
|
| ┅ | 1 |
又知每生产一件正品盈利a元，每生产一件次品损失
元（
）.
(1)将该厂日盈利额T（元）表示为日产量n (件)的一种函数关系式；
（2）为了获得最大盈利，该厂的日产量应定为多少件？
21．（本小题满分12分）
已知点
都在直线
上，
为直线
与轴的交点，数列
成等差数列，公差为1. （
）
(1)求数列，
的通项公式；
(2)若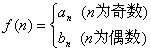
， 问是否存在
，使得
成立；若存在，求出
的值，若不存在，说明理由.
(3)求证：
…… +
(
2, )
22．（本小题满分14分）
已知二次函数
（1）若方程f（x）=0有两实根，且两实根是相邻的两个整数，求证：
（2）若方程f（x）=0有两个非整数实根，且这两实根在相邻两个整数之间，试证明存在整数k,使得
（3）若方程f（x）=0有两个非整数实根，且这两实根不在相邻两个整数之间，请你探求当a,b满足什么条件时，一定存在整数k,使得
成立？
高三数学第一次统测答案2004.10
一． DBDCC， BBACB，CC
二．13．4008 14．（1，+∞） 15.
16.③
三．17．解：（I）
又
函数的定义域为
,
函数的定义域
,
由的定义域为
可知函数为非奇非偶函数,
为偶函数.
（II）设
且
且，
所以
，
，
根据函数单调性的定义知 函数在上为增函数.
18. 解 命题p为真命题
函数的定义域为
对任意的x均成立
时，-x>0解集为；或者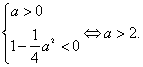
命题q为真命题对一切正实数均成立
对一切正实数均成立.
所以，命题q为真命题
根据题意知，命题p与q为有且只有一个为真命题. 当命题p为真命题且命题q为假命题时a不存在；当命题q为真命题且命题p为假命题时a的取值范围是[1，2].
综上，命题p或q为真命题，命题p且q为假命题，实数a的取值范围是[1，2].
19. 解（1）∵ 
∴ 
，且p＝1，或
．
若是，且p＝1，则由
．
∴ 
，矛盾．故不可能是：，且p＝1．由，得
．
又，∴ 
．
（2）∵ 
，
，
∴ 
．
．
当k≥2时，
． ∴ n≥3时有
．∴ 对一切
有：
．
根据定义证明为等差数列
∵ 
，∴ 
． 
．
故
．
∴ 
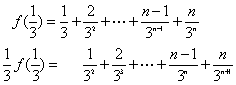两式相减得
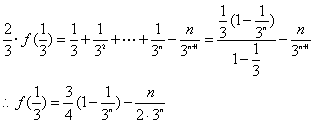
20. 解（1）由题意可知
日产量n 件中，正品（n-pn）件，日盈利额
.
,
当且仅当
，
故
时
取最大值，即
取最大值.
21. 解 (1) 
(2) 
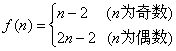
假设存在符合条件的
(ⅰ)若为偶数，则
为奇数，有
如果
，则
与为偶数矛盾.不符舍去；
(ⅱ) 若为奇数，则为偶数，有
这样的也不存在.
综上所述：不存在符合条件的.
(3) 
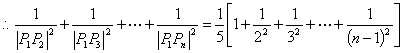
22.（1）证明
设方程f（x）=0两个实根分别为
,
则由题意有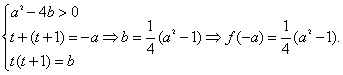
(2）证明
设方程f（x）=0两个实根分别为
，
则有
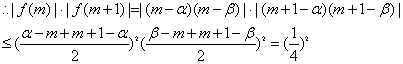
所以必有
故在所给条件下存在整数k=m或m+1,使得
(3)设方程f（x）=0两个实根分别为
令
，必有故此时存在整数k；当
时结论也成立 .
故当a,b满足条件
时，一定存在整数k,使得.