江苏省洪泽中学2006届高三数学期终考试试题
第I卷(选择题 共50分)
一. 选择题:(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的,请将所选答案的标号字母填在题后的括号内)
1. 过点(2,-2)且与双曲线![]() 有相同渐近线的双曲线方程是( )
有相同渐近线的双曲线方程是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.
![]()
2. 把函数![]() 的图像向左平移2个单位,再向下平移1个单位,所得图像的函数解析式为 ( )
的图像向左平移2个单位,再向下平移1个单位,所得图像的函数解析式为 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
3. 若m、n都是正整数,那么“m、n中至少有一个等于1”是“![]() ”的( )
”的( )
A. 充分而不必要的条件 B. 必要而不充分的条件
C. 充要条件 D. 既不充分也不必要的条件
4. 平面向量![]() 则这样的向量
则这样的向量![]() 有 ( )
有 ( )
A.1个 B.2个 C.多个2个 D.不存在
5. 在空间,下列命题正确的是 ( )
A. 若三条直线两两相交,则这三条直线确定一个平面
B. 若直线m与平面![]() 内的一条直线平行,则m//
内的一条直线平行,则m//![]()
C. 若平面![]() ,则过
,则过![]() 内一点P与l垂直的直线垂直于平面
内一点P与l垂直的直线垂直于平面![]()
D. 若直线a//b,且直线![]() ,则
,则![]()
6. 函数![]() 的定义域是
( )
的定义域是
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.
![]()
7. 已知![]() ,且
,且![]() 的值是
( )
的值是
( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
8. 已知F1、F2是椭圆![]() =1(5<a<10)的两个焦点,B是短轴的一个端点,则△F1BF2的面积的最大值是
( )
=1(5<a<10)的两个焦点,B是短轴的一个端点,则△F1BF2的面积的最大值是
( )
A.![]() B.
B.![]() C.100(3-2
C.100(3-2![]() ) D.
) D.![]() a2
a2
9. 已知函数f(x)是定义在R上的奇函数,当x<0时,![]() ,如果
,如果![]() 是f(x)的反函数,则
是f(x)的反函数,则![]() 的值是
( )
的值是
( )
A. ![]() B.
2 C.
B.
2 C.
![]() D.
D.
![]()
10. 已知![]() 是定义在R上的偶函数,且对任意
是定义在R上的偶函数,且对任意![]() ,都有
,都有![]() ,当
,当![]() [4,6]时,
[4,6]时,![]() ,则函数
,则函数![]() 在区间[-2,0]上的反函数
在区间[-2,0]上的反函数![]() 的值
的值![]() 为
( )
为
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第II卷(非选择题 共100分)
二. 填空题:(本大题共6小题,每小题5分,共30分,请把答案直接填在题中横线上) 11. 若x≥0,y≥0,且x+2y=1,则2x+3y2的值域为_____________
12. 若椭圆经过点(2,3),且焦点为![]() ,则这个椭圆的离心率等于_________________。
,则这个椭圆的离心率等于_________________。
13. 一个正方体的全面积为![]() ,它的顶点全都在一个球面上,则这个球的表面积为____。
,它的顶点全都在一个球面上,则这个球的表面积为____。
14. 已知![]() 的夹角的余弦值等于_________________。
的夹角的余弦值等于_________________。
15. 若点![]() ,点
,点![]() ,且
,且![]() ,则过点P且在两坐标轴上有相等截距的直线方程是
。
,则过点P且在两坐标轴上有相等截距的直线方程是
。
16. 定义一种运算“![]() ”为
”为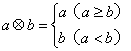 ,那么函数
,那么函数![]() 的值域为_________________。
的值域为_________________。
三. 解答题:(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.解关于x的不等式![]()
18.设向量![]()
![]() ,其中
,其中![]() .
.
(I)求![]() 的取值范围;
的取值范围;
(II)若函数![]() 的大小.
的大小.
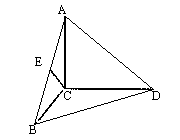
19.如图:已知在![]() 中,
中,![]() ,BC=CD=1,
,BC=CD=1,![]() 平面BCD,
平面BCD,![]() ,E是AB的中点。
,E是AB的中点。
(I)求直线BD和CE所成的角;
(II)求点C到平面ABD的距离;
(III)若F是线段AC上的一个动点,请确定点F的位置,使得平面![]() 平面DEF。
平面DEF。
20.已知倾斜角为![]() 的直线
的直线![]() 过点
过点![]() 和点
和点![]() ,其中
,其中![]() 在第一象限,且
在第一象限,且![]()
(Ⅰ)求点![]() 的坐标;
的坐标;
(Ⅱ)若直线![]() 与双曲线
与双曲线![]()
![]() 相交于不同的两点
相交于不同的两点![]() ,且线段
,且线段![]() 的中点坐标为
的中点坐标为![]() ,求实数
,求实数![]() 的值。
的值。
21. 某森林出现火灾,火势正以每分钟![]() 的速度顺风蔓延,消防站接到警报立即派消防队员前去,在火灾发生后五分钟到达救火现场,已知消防队员在现场平均每人每分钟灭火
的速度顺风蔓延,消防站接到警报立即派消防队员前去,在火灾发生后五分钟到达救火现场,已知消防队员在现场平均每人每分钟灭火![]() ,所消耗的灭火材料、劳务津贴等费用为每人每分钟125元,另附加每次救火所耗损的车辆、器械和装备等费用平均每人100元,而烧毁一平方米森林损失费为60元.问应该派多少消防队员前去救火,才能使总损失最少?
,所消耗的灭火材料、劳务津贴等费用为每人每分钟125元,另附加每次救火所耗损的车辆、器械和装备等费用平均每人100元,而烧毁一平方米森林损失费为60元.问应该派多少消防队员前去救火,才能使总损失最少?
22.在直角坐标平面上有一点列![]() ,对每个正整数
,对每个正整数![]() ,点
,点![]() 位于函数
位于函数![]() 的图象上,且
的图象上,且![]() 的横坐标构成以
的横坐标构成以![]() 为首项,
为首项,![]() 为公差的等差数列
为公差的等差数列![]() 。
。
(1)求点![]() 的坐标;
的坐标;
(2)设抛物线列![]() 中的每一条的对称轴都垂直于
中的每一条的对称轴都垂直于![]() 轴,第
轴,第![]() 条抛物线
条抛物线![]() 的顶点为
的顶点为![]() 且过点
且过点![]() ,记过点
,记过点![]() 且与抛物线
且与抛物线![]() 只有一个交点的直线的斜率为
只有一个交点的直线的斜率为![]() ,求证:
,求证:![]() ;
;
(3)设![]() ,
,![]() ,等差数列
,等差数列![]() 的任一项
的任一项![]() ,其中
,其中![]() 是
是![]() 中的最大数,
中的最大数,![]() ,求
,求![]() 的通项公式。
的通项公式。
参考答案及评分标准
一. 选择题:(每小题5分,共50分)
1. D 2. B 3. C 4. A 5. D 6. B 7. A 8. B 9. B 10. B
二. 填空题:(每小题5分,共30分)
11. [![]() ,2]12.
,2]12. ![]() ; 13.
; 13.
![]() ; 14.
; 14. ![]() 15.
15.
![]() 或
或![]()
16. ![]()
三. 解答题:(共70分,以下各题为累计得分,其他解法请相应给分)
17. 解:①当a=0时,化为![]() …………2分
…………2分
解集为![]() …………3分
…………3分
②当a>0时原不等式等价于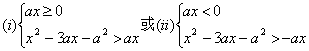 …5分
…5分
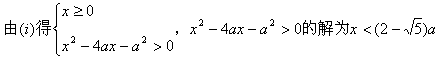
![]() …………7分
…………7分
![]()
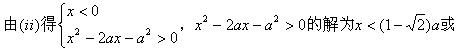
![]() …………9分
…………9分
![]()
![]() ,a>0时,解集为
,a>0时,解集为![]()
![]()
18. 解:(I)∵![]() (2分)
(2分)
∴![]() ,
(4分)
,
(4分)
∵![]() ,∴
,∴![]()
∴![]() ,∴
,∴![]() 。
(6分)
。
(6分)
(II)∵![]() ,
,
![]() , (8分)
, (8分)
∴![]() ,
(10分)
,
(10分)
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() 。 (12分)
。 (12分)
19. 解:(I)延长AC到G,使CG=AC,连结BG、DG,E是AB中点
![]()
故直线BG和BD所成的锐角(或直角)就是CE和BD所成的角……2分

(II)设C到平面ABD的距离为h
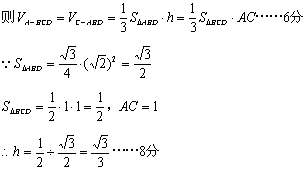

20. 解:(Ⅰ) 直线![]() 方程为
方程为![]() ,设点
,设点![]() ,
(2分)
,
(2分)
由![]() (4分)
(4分)
及![]() ,得
,得![]() ,
,
∴点![]() 的坐标为
的坐标为![]() (6分)
(6分)
(Ⅱ)由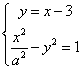 得
得![]() ,
(8分)
,
(8分)
设![]() ,则
,则![]() ,得
,得![]() , (11分)
, (11分)
此时,![]() ,∴
,∴![]() 。
(12分)
。
(12分)
(注:缺少![]() 扣1分,
扣1分,![]() 这个不等式可解可不解。)
这个不等式可解可不解。)
21. 解:设派x名消防员前去救火,用t分钟将火扑灭,总损失为y,则
![]()
y=灭火劳务津贴+车辆、器械装备费+森林损失费
=125tx+100x+60(500+100t)
=![]()
=![]()
=![]()
![]()
当且仅当![]() ,即x=27时,y有最小值36450.
,即x=27时,y有最小值36450.
故应该派27名消防员前去救火,才能使总损失最少,最少损失为36450元.
22. 解:(1)∵![]() 的横坐标构成以
的横坐标构成以![]() 为首项,
为首项,![]() 为公差的等差数列
为公差的等差数列![]() ,
,
∴![]() , (2分)
, (2分)
∵![]() 位于函数
位于函数![]() 的图像上,
的图像上,
∴![]() , (3分)
, (3分)
∴点![]() 的坐标为
的坐标为![]() 。 (4分)
。 (4分)
(2)据题意可设抛物线![]() 的方程为:
的方程为:![]() ,
,
即![]() ,
(5分)
,
(5分)
∵抛物线![]() 过点
过点![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() , (6分)
, (6分)
∵过点![]() 且与抛物线
且与抛物线![]() 只有一个交点的直线即为以
只有一个交点的直线即为以![]() 为切点的切线,
为切点的切线,
∴![]() , (7分)
, (7分)
∴![]() (
(![]() )
)
∴![]()
![]()
∴![]()
![]() 。 (8分)
。 (8分)
(3)∵![]() ,
,![]()
∴![]() 中的元素即为两个等差数列
中的元素即为两个等差数列![]() 与
与![]() 中的公共项,它们组成以
中的公共项,它们组成以![]() 为首项,以
为首项,以![]() 为公差的等差数列,
(9分)
为公差的等差数列,
(9分)
∵![]() ,且
,且![]() 成等差数列,
成等差数列,![]() 是
是![]() 中的最大数,
中的最大数,
∴![]() ,其公差为
,其公差为![]() ,
,
10当![]() 时,
时,![]() ,
,
此时![]() ,∴不满足题意,舍去;(10分)
,∴不满足题意,舍去;(10分)
20当![]() 时,
时,![]() ,
,
此时![]() ,
,
∴![]() ;
;
30当![]() 时,
时,![]() ,
,
此时![]() ,∴不满足题意,舍去。(12分)
,∴不满足题意,舍去。(12分)
综上所述所求通项为![]() 。
。