涡阳四中高三第一次月考
数学试题(文)
2006.8
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。共150分,考试用时120分钟。
(第Ⅰ卷选择题部分,共50分)
一、 选择题:(本大题共10小题,每个小题5分,共50分,在每小题给出的四个选项中,只有一个是符合要求的)
1、已知集合![]() ,则集合
,则集合![]() = ( )
= ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2、已知a,b为实数,集合M={,1},N={a,0},f:x→x表示把M中的元素x映射到集合N中仍为x,则a+b等于
A![]() -1 B
-1 B![]() 0 C
0 C![]() 1 D
1 D![]() ±1
±1
3、若不等式![]() ,则实数a= ( )
,则实数a= ( )
A.0 B.-4 C.-6 D.-8
4、.试在下列四个命题中找出一个与命题“无火不冒烟”等价的命题 ( )
A.若有火必冒烟 B.虽无火但有可能冒烟
C.冒烟处必有火 D.虽无烟但可能有火
5、设函数![]() 是定义在R上,周期为3的奇函数若
是定义在R上,周期为3的奇函数若![]() ,
,![]() 则 ( )
则 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6、已知函数![]() ,
,![]() ,则
,则![]() 等于( )
等于( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7、已知函数![]() 是R上的偶函数,
是R上的偶函数,![]() 是R上的奇函数,且
是R上的奇函数,且![]() ,若
,若![]() ,
,
则![]() 的值为 ( )
的值为 ( )
A.2 B.0 C.—2 D.±2
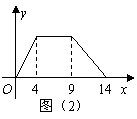
8、直角梯形ABCD如图(1),动点P从B点出发,由![]() 沿边运动,设点P运动的路程为x,
沿边运动,设点P运动的路程为x,![]() 的面积为
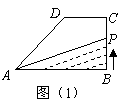
的面积为![]() .如果函数
.如果函数![]() 的图象如图(2),则
的图象如图(2),则![]() 的面积为 ( )
的面积为 ( )
 | |||
 | |||
A.10 B.16 C.18 D.32
9、若一系列函数的解析式相同,值域相同,但其定义域不同,则称这些函数为“同族函数”,那么函数解析式为y=x2,值域为{1,4}的“同族函数”共有
A.7个 B.8个 C.9个 D.10个
10、能成为a>1的必要非充分条件的是 ( )
(1)函数![]() 上是减函数
上是减函数
(2)![]()
(3)![]()
(4)![]()
A.(1)(2) B.(3)(4) C.(2)(3) D.(2)(4)
第Ⅱ卷(非选择题部分,共100分)
二、填空题:(本题共5个小题,每小题4分,共20分。)
11、已知函数![]() .
.
12、设![]() {1,2,3,4,5,6},A与B是
{1,2,3,4,5,6},A与B是![]() 的子集,若
的子集,若![]() ={1,3,5},则称
={1,3,5},则称
(A,B)为“理想配集”,所有“理想配集”的个数是 .
13、已知函数y=f(x)的定义域是[0,2],且![]() ,那么函数
,那么函数![]() 的定义域是_____________________
的定义域是_____________________![]()
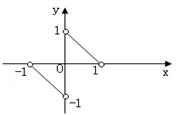 14、已知函数
14、已知函数![]() 的图象如图,则不等式
的图象如图,则不等式![]() 的解集为
。
的解集为
。
15已知x∈N*,f(x)= 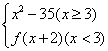 ,其值域设为D,给出下列数值:-26,-1,9,14,27,65,则其中属于集合D的元素是_________.
,其值域设为D,给出下列数值:-26,-1,9,14,27,65,则其中属于集合D的元素是_________.
(写出所有可能的数值)
三、解答题:(本大题共6小题,共80分,解答应写出文字说明、证明过程或演算步骤。)
16、(本小题满分12分)
设函数![]() ,不等式
,不等式![]() 的解集为
的解集为![]() ,
,
试求不等式![]() 的解集
的解集
17、(本小题满分12分)
已知函数![]() =
=![]() ,
,![]() (a为正常数),
(a为正常数),
且函数![]() 与
与![]() 的图象在y轴上的截距相等.
的图象在y轴上的截距相等.
(1)求a的值;
(2)求函数![]() -
-![]() 的单调递增区间.
的单调递增区间.
18. (本小题满分14分)
通过研究学生的学习行为,专家发现,学生的注意力随着老师讲课时间的变化而变化,
讲课开始时,学生的兴趣激增;中间有一段时间,学生的兴趣保持较理想的状态,随
后学生的注意力开始分散. 设![]() 表示学生注意力随时间t(分钟)的变化规律(
表示学生注意力随时间t(分钟)的变化规律(![]()
越大,表明学生注意力越集中),经过实验分析得知:

(1)讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟?
(2)有一道数学难题,需要讲解24分钟,并且要求学生的注意力至少达到180,那么
老师能否在学生达到所需的状态下讲授完这道题目?若能,老师如何安排讲解时
间;若不能,说明理由.
19.(本小题满分14分)
已知点A(7,0)在曲线![]() 上,且曲线C在点A处的切线与直线
上,且曲线C在点A处的切线与直线![]() 垂直,又当
垂直,又当![]() 时,函数
时,函数![]() 有最小值.
有最小值.
(I)求实数a,b,c的值;
(II)设函数![]() 的最大值为M,
的最大值为M,
求正整数![]() 的值,使得
的值,使得![]() 成立.
成立.
20(本小题满分14分)![]()
函数![]() 是定义域为R的偶函数,且对任意的
是定义域为R的偶函数,且对任意的![]() ,均有
,均有![]() 成立.当
成立.当![]() 时,
时,![]()
(1)当![]() 时,求
时,求![]() 的表达式;
的表达式;
(2)若![]() 的最大值为
的最大值为![]() ,解关于x的不等式
,解关于x的不等式![]() .
.
21、(本小题满分14分)
已知二次函数f(x)满足f(-1)=0,且 8x![]() f(x)
f(x)![]() 4(x2+1) 对
4(x2+1) 对![]() 恒成立
恒成立
(1)求函数y=f(x)的解析式;
(2)利用函数g(x)=![]() 的定义域为D,构造一个数列{xn},方法如下:
的定义域为D,构造一个数列{xn},方法如下:
对于给定的定义域中的x1,令x2= g(x1),x3=g(x2),…,xn= g(xn-1),…
在上述构造过程中,如果xi(i=1,2,3,…)在定义域D中,构造数列的过程继续下去;如果xi不在定义域中,则构造数列的过程停止.
如果X1=![]() ,请求出满足上述条件的数列{xn}的集合M={x1,x2,…,xn}
,请求出满足上述条件的数列{xn}的集合M={x1,x2,…,xn}
22、已知![]() 上是减函数,且
上是减函数,且![]() 。
。
(1)求![]() 的值,并求出
的值,并求出![]() 和
和![]() 的取值范围。
的取值范围。
(2)求证![]() 。
。
(3)求![]() 的取值范围,并写出当
的取值范围,并写出当![]() 取最小值时的
取最小值时的![]() 的解析式。
的解析式。
参考答案(文)
一,选择题:
D C B CC, CA BC B
二、填空题:
(11),
-3![]() ,
(12), 27
(13),
,
(12), 27
(13), ![]()
(14), ![]() . (15), -26,14,65
. (15), -26,14,65
三、解答题:
16, 由已知得![]() ;所以解集:
;所以解集:![]() ;
;
17, (1)由题意![]() ,
,![]() =1又a>0,所以a=1.
=1又a>0,所以a=1.
(2)![]()
![]() g(x)=
g(x)=![]() ,当
,当![]() 时,
时,![]()
![]()
![]() =
=![]() ,无递增区间;当x<1时,
,无递增区间;当x<1时,![]()
![]()
![]() =
=![]() ,它的递增区间是
,它的递增区间是![]() .
.
综上知:![]()
![]()
![]() 的单调递增区间是
的单调递增区间是![]() .
.
18, (1)当0<t≤10时,
![]() 是增函数,且f(10)=240
是增函数,且f(10)=240
当20<t≤40时,![]() 是减函数,且f(20)=240 所以,讲课开始10分钟,学生的注意力最集中,能持续10分钟。(3)当0<t≤10时,令
是减函数,且f(20)=240 所以,讲课开始10分钟,学生的注意力最集中,能持续10分钟。(3)当0<t≤10时,令![]() ,则t=4 当20<t≤40时,令
,则t=4 当20<t≤40时,令![]() ,则t≈28.57
,则t≈28.57
则学生注意力在180以上所持续的时间28.57-4=24.57>24
从而教师可以第4分钟至第28.57分钟这个时间段内将题讲完。
19, (I)![]() ……1分
……1分
根据题意,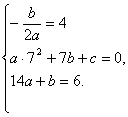 …………4分
…………4分
解得![]() . …………7分
. …………7分
(II)因为![]() ……7分
……7分
(i)![]() 时,函数
时,函数![]() 无最大值,
无最大值,
不合题意,舍去. …………11分
(ii)![]() 时,根据题意得
时,根据题意得
![]()
解之得![]() …………13分
…………13分
![]() 为正整数,
为正整数,![]() =3或4. …………14分
=3或4. …………14分
20. (1)当x∈[-1,0)时, f(x)= f(-x)=loga[2-(-x)]=loga(2+x).
当x∈[2k-1,2k),(k∈Z)时,x-2k∈[-1,0], f(x)=f(x-2k)=loga[2+(x-2k)].
当x∈[2k,2k+1](k∈Z)时,x-2k∈[0,1], f(x)=f(x-2k)=loga[2-(x-2k)].
故当x∈[2k-1,2k+1](k∈Z)时, f(x)的表达式为
|
loga[2-(x-2k)],x∈[2k,2k+1].
(2)∵f(x)是以2为周期的周期函数,且为偶函数,∴f(x)的最大值就是当x∈[0,1]时f(x)的最大值,∵a>1,∴f(x)=loga(2-x)在[0,1]上是减函数,
∴[f(x)]max= f(0)=![]() =
=![]() ,∴a=4.
,∴a=4.
当x∈[-1,1]时,由f(x)>![]() 得
得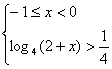
或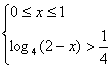 得
得![]()
∵f(x)是以2为周期的周期函数,
∴f(x)>![]() 的解集为{x2k+
的解集为{x2k+![]() -2<x<2k+2-
-2<x<2k+2-![]() ,k∈Z
,k∈Z
21.(1)由8x![]() f(x)
f(x)![]() 4(x2+1),∴f(1)=8,f(-1)=0,∴b=4
4(x2+1),∴f(1)=8,f(-1)=0,∴b=4
又8x![]() f(x)
f(x)![]() 4(x2+1) 对
4(x2+1) 对![]() 恒成立,∴a=c=2 f(x)=2(x+1)2
恒成立,∴a=c=2 f(x)=2(x+1)2
(2)∵g(x)=![]() =
=![]() ,D={x︱x
,D={x︱x![]() -1 }
-1 }
X1=![]() ,x2=
,x2=![]() ,x3=-
,x3=-![]() ,x4=-1,∴M={
,x4=-1,∴M={![]() ,
,![]() ,-
,-![]() ,-1}
,-1}
22、(1)![]()
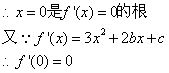
![]() ··············································2分
··············································2分

![]() ·············································5分
·············································5分
(2)![]()

![]() ··········································10分
··········································10分
(3)![]()
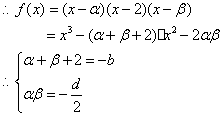
·······················································12分

![]() ··································15分
··································15分