无锡市辅仁高中高三数学测试06.02.21
姓名 班级
一、选择题(每小题5分,共10小题,共50分)
1.已知![]() ,全集U=R,集合M=
,全集U=R,集合M=![]() ,N=
,N=![]() ,P=
,P=![]() ,则P与M、N的关系为 ( )
,则P与M、N的关系为 ( )
A.P= (CUM) ![]() N B.P=M
N B.P=M![]() (CUN) C.P=M
(CUN) C.P=M![]() N D.P=M
N D.P=M![]() N
N
2.等差数列![]() 的通项公式是
的通项公式是![]() ,其前
,其前![]() 项和为
项和为![]() ,则数列
,则数列![]() 的前10项和为 ( )
的前10项和为 ( )
A.75 B.70 C.120 D.100
3.先将![]() 的图象沿
的图象沿![]() 轴向右平移
轴向右平移![]() 个单位,再将图象上每一个点的横坐标伸长为原来的2倍,而保持它们的纵坐标不变,得到的曲线与
个单位,再将图象上每一个点的横坐标伸长为原来的2倍,而保持它们的纵坐标不变,得到的曲线与![]() 的图象相同,则
的图象相同,则![]() 是
( )
是
( )
A.![]() B.
B. ![]()
C.![]() D.
D.![]()
4.已知直线![]() 、
、![]() 和平面
和平面![]() ,则
,则![]() 的一个必要不充分条件是 ( )
的一个必要不充分条件是 ( )
A. ![]() ,
,![]() B.
B.![]() ,
,![]()
C. ![]() ,
,![]() D.
D.![]() 、
、![]() 与
与![]() 成等角
成等角
5.函数![]() 在其定义域上单调递减,且值域为
在其定义域上单调递减,且值域为![]() ,则它的反函数的值域是
( )
,则它的反函数的值域是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 边上的高,若
边上的高,若![]() ,则实数
,则实数![]() 的值等于
( )
的值等于
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
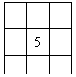 7.将1-9这9个不同的数字分别填入右图中的方格中,要求每行自左至右数字从小到大排,每列自上到下数字也从小到大排,并且5排在正中的方格,则不同的填法共有
( )
7.将1-9这9个不同的数字分别填入右图中的方格中,要求每行自左至右数字从小到大排,每列自上到下数字也从小到大排,并且5排在正中的方格,则不同的填法共有
( )
A.24种 B.20种 C.18种 D.12种
8.圆![]() 与圆
与圆![]() 关于直线
关于直线![]() 对称,则
对称,则![]() 与
与![]() 的值分别等于
( )
的值分别等于
( )
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
9. ![]() 为三角形的一个内角,且
为三角形的一个内角,且![]() ,则
,则![]() 与
与![]() 的值依次为 (
)
的值依次为 (
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.已知椭圆![]() 与双曲线
与双曲线![]() 有相同的焦点
有相同的焦点![]() 和
和![]() .若
.若![]() 是
是![]() 与
与![]() 的等比中项,
的等比中项,![]() 是
是![]() 与
与![]() 的等差中项,则椭圆的离心率等于
( )
的等差中项,则椭圆的离心率等于
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题:本大题共6小题,每小题4分,共24分;把答案题中的横线上.
11.设![]() 的展开式的各项系数之和为M,且二项式系数之和为N,M—N=992,则展开式中x2项的系数为 .
的展开式的各项系数之和为M,且二项式系数之和为N,M—N=992,则展开式中x2项的系数为 .
12.设![]() ,定义
,定义![]() ,且
,且![]() ,则
,则![]()
13.一个总体中有100个个体,随机编号0,1,2,…,99,依编号顺序平均分成10个小组,组号依次为1,2,3,…,10.现用系统抽样方法抽取一个容量为10的样本,规定如果在第1组随机抽取的号码为m,那么在第k组中抽取的号码个位数字与m+k的个位数字相同,若m=6,则在第7组中抽取的号码是 .(63)
14.有下列四个命题:
①函数![]() 的值域是
的值域是![]() ;
;
②平面内的动点P到点F![]() 和到直线
和到直线![]() :
:![]() 的距离相等,则P的轨迹是抛物线;
的距离相等,则P的轨迹是抛物线;
③直线AB与平面![]() 相交于点B,且AB与
相交于点B,且AB与![]() 内相交于C的三条互不重合的直线CD、CE、CF所成的角相等,则AB
内相交于C的三条互不重合的直线CD、CE、CF所成的角相等,则AB![]() ;
;
④函数![]() 的最小正周期是
的最小正周期是![]() .
.
其中正确的命题的编号是 .
15.如果三棱锥的三个侧面两两垂直,它们的面积分别为6![]() 、4
、4![]() 和3
和3![]() ,那么它的外接球的体积是
.
,那么它的外接球的体积是
.
16.已知函数![]() 的图象是平面上到两定点距离之差的绝对值等于定长的点的轨迹,则这个定长为
.
的图象是平面上到两定点距离之差的绝对值等于定长的点的轨迹,则这个定长为
.
三、解答题:本大题6小题,共76分.解答应写出文字说明,证明过程或演算步骤.
17.( 12分)在袋里装30个小球,其中彩球有:n个红色、5个蓝色、10个黄色,其余为白球. 求:
(Ⅰ)如果已经从中取定了5个黄球和3个蓝球,并将它们编上了不同的号码后排成一排,那么使蓝色小球互不相邻的排法有多少种?(用数字作答)
(Ⅱ)如果从袋里取出3个都是相同颜色彩球(无白色)的概率是![]() ,且n≥2,计算红球有几个?
,且n≥2,计算红球有几个?
18.( 12分)已知向量![]()
(Ⅰ)向量![]() 是否共线?请说明理由.
是否共线?请说明理由.
(Ⅱ)求函数![]() 的最大值.
的最大值.
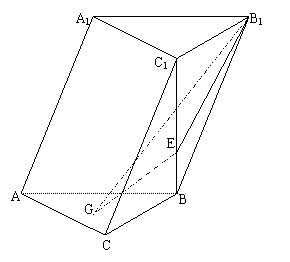 19.( 12分)如图,在斜三棱柱ABC-A1B1C1中,侧面AA1B1B
19.( 12分)如图,在斜三棱柱ABC-A1B1C1中,侧面AA1B1B![]() 底面ABC,侧棱AA1与底面ABC成
底面ABC,侧棱AA1与底面ABC成![]() 角,AA1=2,底面ABC是边长为2的正三角形,其重心为G点,E是线段BC1上一点,且BE=
角,AA1=2,底面ABC是边长为2的正三角形,其重心为G点,E是线段BC1上一点,且BE=![]() BC1
BC1
(Ⅰ)求证:GE//侧面AA1B1B;
(Ⅱ)求平面B1GE与底面ABC所成锐二面角的大小。
20.( 12分)已知函数![]() ,且函数
,且函数![]() 的图像关于原点对称,其图像在x=3处的切线方程为8x-y-18=0。
的图像关于原点对称,其图像在x=3处的切线方程为8x-y-18=0。
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)是否存在区间[a,b],使得函数g(x)的定义域和值域均为[a,b],且解析式与![]() 的解析式相同?若存在,求出这样的一个区间[a,b];若不存在,请说明理由。
的解析式相同?若存在,求出这样的一个区间[a,b];若不存在,请说明理由。
21.( 14分)已知曲线![]() ,过
,过![]() 上的点
上的点![]() 作曲线
作曲线![]() 的切线
的切线![]() 交
交![]() 轴于点
轴于点![]() ,再过点
,再过点![]() 作
作![]() 轴的平行线交曲线
轴的平行线交曲线![]() 于点
于点![]() ,再过点
,再过点![]() 作曲线
作曲线![]() 的切线
的切线![]() 交
交![]() 轴于点
轴于点![]() ,再过点
,再过点![]() 作
作![]() 轴的平行线交曲线
轴的平行线交曲线![]() 于点
于点![]() ,……,依次作下去,记点
,……,依次作下去,记点![]() 的横坐标为
的横坐标为![]()
![]()
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)设数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证:![]()
(Ⅲ)求证:![]() 。
。
22.( 14分)F1、F2分别是双曲线![]() 的两个焦点,O为坐标原点,圆O是以F1F2为直径的圆,直线
的两个焦点,O为坐标原点,圆O是以F1F2为直径的圆,直线![]() 与圆O相切,并与双曲线交于A、B两点. 向量
与圆O相切,并与双曲线交于A、B两点. 向量![]() 在向量
在向量![]() 方向的投影是p.
方向的投影是p.
(Ⅰ)根据条件求出b和k满足的关系式;
(Ⅱ)当![]() 时,求直线l的方程;
时,求直线l的方程;
(Ⅲ)当![]() 时,求
时,求![]() 面积的取值范围.
面积的取值范围.
参考答案
填空 :-250;![]() ;63;3、4;
;63;3、4;![]() ;
;![]()
17、解:(Ⅰ)将5个黄球排成一排只有![]() 种排法,将3个蓝球放在5个黄球所形成的6个空上,有
种排法,将3个蓝球放在5个黄球所形成的6个空上,有![]() 种放法 ,
种放法 ,
∴所求的排法为![]() =5×4×3×2×6×5×4=14400(种).
4分
=5×4×3×2×6×5×4=14400(种).
4分
(Ⅱ)取3个球的种数为![]() =4060,设“3个球全红色”为事件A,“3个球全蓝色”为事件B,“3个球全黄色”为事件C.
=4060,设“3个球全红色”为事件A,“3个球全蓝色”为事件B,“3个球全黄色”为事件C.
P(B)=![]() ,
,
∵A、B、C为互斥事件,
∴P(A+B+C)= P(A)+P(B)+P(C),
即![]()
![]() 取3个球红球的个数n≤2.
取3个球红球的个数n≤2.
又∵n≥2,故n = 2 .
18.解:(Ⅰ)![]() 共线.……(1分)
共线.……(1分)
![]() ,
,
∴![]() 共线.………………(5分)
共线.………………(5分)
(Ⅱ)![]() ……(7分)
……(7分)
![]() ………………(8分)
………………(8分)
又![]() ……(10分)
……(10分)
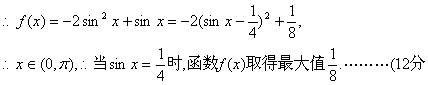
20、解:(1)![]()
![]() 的图像关于原点对称,
的图像关于原点对称,![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,![]() 。
。![]() ,
,![]()
又![]() 的图像在x=3处的切线方程为
的图像在x=3处的切线方程为![]() ,
,
即![]() ,据题意得:
,据题意得:![]() 解得:
解得: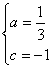 ,
,
![]()
(2)由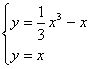 得x=0或
得x=0或![]() 。
。
又![]() ,由
,由![]() 得
得![]() ,且当
,且当![]() 或
或![]() 时,
时,![]() ,当
,当![]() 时
时![]() 。
。
所以,函数![]() 在
在![]() 和
和![]() 上递增,在
上递增,在![]() 上递减。
上递减。
于是,函数在![]() 上的极大值和极小值分别为
上的极大值和极小值分别为
![]() ,
,![]() 而
而![]() ,
,
故存在这样的区间[a,b],其中满足条件的一个区间![]()
21、21、解(1)![]() 曲线
曲线![]() 在点
在点![]() 处的切线
处的切线![]() 的斜率是
的斜率是![]() ,
,![]() 切线
切线![]() 的方程是
的方程是![]() ,由于点
,由于点![]() 的横坐标等于点
的横坐标等于点![]() 的横坐标
的横坐标![]() ,所以,令
,所以,令![]() ,
,
得![]() ,
,![]() 数列
数列![]() 是首项为1,公比为
是首项为1,公比为![]() 的等比数列,
的等比数列,![]()
(2)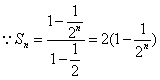 ,
,![]() ,令
,令![]() ,则
,则![]()
![]()
![]() 当
当![]() ,即
,即![]() 时,
时,![]() 有最大值1,即
有最大值1,即![]()
(3)![]() ,
,![]() ,即
,即![]() ,
,
![]() 数列
数列![]() 是首项为1,公比为4的等比数列
是首项为1,公比为4的等比数列
![]()
22、解(1)双曲线![]() 的两个焦点分别是
的两个焦点分别是![]() ,从而圆O的方程为
,从而圆O的方程为![]() 由于直线
由于直线![]() 与圆O相切,所以有
与圆O相切,所以有![]()
即![]() 为所求.
(3分)
为所求.
(3分)
(2)设![]() 则由
则由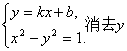 并整理得,
并整理得,
![]()
根据韦达定理,得![]() (5分)
(5分)
从而![]()
![]()
又由(1)知![]()
又由于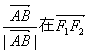 方向上的投影为p,所以
方向上的投影为p,所以
![]()
即![]() (8分)
(8分)
![]()
所以直线l的方程为![]() (9分)
(9分)
(3)类似于(2)可得 ![]()
即![]()
![]() (10分)
(10分)
根据弦长公式,得
![]()
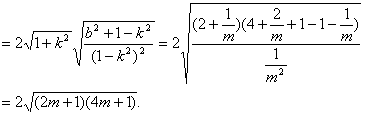
![]()
![]()
而![]()
![]()
当![]()
因此△AOB面积的取值范围是![]() (14分)
(14分)