西北师大附属中学2006届高三毕业班
数学基础能力综合测试(三)
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
1、若![]() ( )
( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限
2、已知集合![]() ( )
( )
A、1 B、2 C、1或2 D、8
3、函数![]() 的定义域为 ( )
的定义域为 ( )
A、![]() B、
B、![]() C、(1,2) D、
C、(1,2) D、![]()
4、设![]() ,则下列不等式成立的是 ( )
,则下列不等式成立的是 ( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
5、某地区高中分三类,A类校共有学生4000人,B类校共有学生2000人,C类校共有学生3000人.现欲抽样分析某次考试的情况,若抽取900份试卷进行分析,则从A类校抽取的试卷份数应为( )
A、450 B、400 C、300 D、200
|
A、![]() B、
B、![]()
C、![]() D、
D、![]()
7、实数![]() ( )
( )
A、![]() B、
B、![]() C、9 D、10
C、9 D、10
8、已知F1、F2为双曲线![]() 的焦点,过F2作垂直于x轴的直线,它与双曲线的一个交点为P,且
的焦点,过F2作垂直于x轴的直线,它与双曲线的一个交点为P,且![]() ,则双曲线的渐近线方程为 ( )
,则双曲线的渐近线方程为 ( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
9、已知![]() ,其中
,其中![]() 则满足条件的不共线的向量共有( )
则满足条件的不共线的向量共有( )
A、16个 B、13个 C、12个 D、9个
10、在棱长为2的正方体AC1中,点E,F分别是棱AB,BC的中点,则点C1到平面B1EF的距离是
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
11、已知f(x)是定义在R上的奇函数,且满足![]()
![]() ,则使
,则使![]() 的
的![]() 值等于 ( )
值等于 ( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
12、甲、乙两人同时从A地出发沿同一路线走到B地,所用时间分别为t1,t2,甲有一半时间以速度m行走,另一半时间以速度n行走(m≠n);乙有一半路程以速度m行走,另一半路程以速度n行走,则下列结论成立的是 ( )
A、t1>t2 B、t1=t2 C、t1<t2 D、t1,t2的大小无法确定
二、填空题:把答案填在题中横线上.
13、设抛物线![]() 则P到抛物线焦点F的距离为 .
则P到抛物线焦点F的距离为 .
14、给出下列四个命题:①若命题“p:x>2”为真命题,则命题“q:x≥2”为真命题;②如果一个简单多面体的所有面都是四边形,那么F=V-2(其中F是面数,V是顶点数);③函数![]() ④在
④在![]()
其中所有正确命题的序号是 .
![]()
![]() 15、设
15、设![]() “ ”为
“ ”为![]()
![]() =
=![]()
![]() ,若已知
,若已知![]() ,
,![]()
![]()
![]() ,则
,则![]() =
.
=
.
16、等差数列{an}的前n项和为Sn,且![]() 如果存在正整数M,使得对一切正整数n,
如果存在正整数M,使得对一切正整数n,![]() 都成立.则M的最小值是
.
都成立.则M的最小值是
.
三、解答题:解答应写出文字说明,证明过程或演算步骤.
17、已知![]() 是两个不共线的向量,且
是两个不共线的向量,且![]() .
.
(Ⅰ)求证:![]() 与
与![]() 垂直;
垂直;
(Ⅱ)若![]() ,且
,且![]() ,求
,求![]() 的值。
的值。
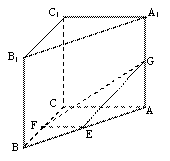 18、如图,在直三棱柱ABC—A1B1C1中,AC=BC=AA1,∠ACB=90°,E、F分别是AB、BC的中点,G是AA1上的点.
18、如图,在直三棱柱ABC—A1B1C1中,AC=BC=AA1,∠ACB=90°,E、F分别是AB、BC的中点,G是AA1上的点.
(Ⅰ)如果![]() ,试确定点G的位置;
,试确定点G的位置;
(Ⅱ)在满足条件(Ⅰ)的情况下,试求![]()
19、甲、乙、丙三人分别独立解一道题,甲做对的概率是![]() ,甲、乙、丙三人都做对的概率是
,甲、乙、丙三人都做对的概率是![]() 甲、乙、丙三人全做错的概率是
甲、乙、丙三人全做错的概率是![]()
(Ⅰ)分别求乙、丙两人各自做对这道题的概率;
(Ⅱ)求甲、乙、丙三人中恰有一人做对这道题的概率.
20、已知等差数列{an},公差大于0,且![]() 的两根,数列{bn}前n项和为Tn,且
的两根,数列{bn}前n项和为Tn,且![]()
(Ⅰ)写出数列{an}、{bn}的通项公式;
(Ⅱ)记![]() .
.
21、平面内动点M与点![]() 所成直线的斜率分别为k1、k2,且满足
所成直线的斜率分别为k1、k2,且满足![]()
(Ⅰ)求点M的轨迹E的方程,并指出E的曲线类型;
(Ⅱ)设直线:![]() 分别交x、y轴于点A、B,交曲线E于点C、D,且AC=BD.(1)求k的值;(2)若点
分别交x、y轴于点A、B,交曲线E于点C、D,且AC=BD.(1)求k的值;(2)若点![]() ,求△NCD面积取得最大时直线l的方程.
,求△NCD面积取得最大时直线l的方程.
参考答案
一、选择题:BCDCB ADDCB AC
二、填空题:13、4 14、①②④ 15、(-2,1) 16、2
三、解答题:17、解:(Ⅰ)(解法一)![]() ,
,![]()
(解法二)![]() ,
,![]()
![]()
![]()
(Ⅱ)![]()
![]() .
.
18、解:(Ⅰ)以C为原点,![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.
设AC=2,则C(0,0,0),A(0,2,0),C1(0,0,2)E(1,1,0)
设![]()
由![]() 即点
即点![]() 为
为![]() 的中点。
的中点。
(Ⅱ)![]() .
. ![]()
19、解:(Ⅰ)分别记甲、乙、丙三人各自全做对这张试卷分别为事件![]() ,则
,则![]() ,根据题意得
,根据题意得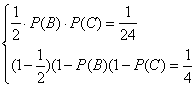
解得![]() 或
或![]()
答:乙、丙两人各自全做对这张试卷的概率分别为![]() 。(若少一解,则扣1分)
。(若少一解,则扣1分)
(Ⅱ)记“甲、乙、丙三人中恰有一人做对这道题”为事件D,则
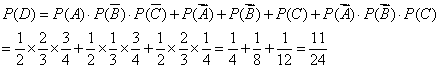
答:甲、乙、丙三人中恰有一人做对这道题的概率为![]()
20、解:(Ⅰ)由题意得![]()
又因为等差数列的公差大于零,![]() ,
,![]()
由![]()
当![]() 时,
时,![]() ,
,![]()
(Ⅱ)![]() ,
,![]() 。
。
21、解:(Ⅰ)设动点M的坐标为![]() ,
,![]() ,即
,即![]()
动点M的轨迹E是中心在原点,半长轴为2,焦点为(![]() )的椭圆(除去长轴两个端点.)它的方程是
)的椭圆(除去长轴两个端点.)它的方程是![]() 。
。
(Ⅱ)(1)在![]()
![]() 的中点为
的中点为![]()
设![]() ,由
,由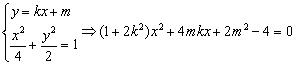
![]() ,∵
,∵![]() ,∴
,∴![]() 中点就是
中点就是![]() 中点,即
中点,即![]()
![]()
点![]() 到
到![]() 的距离
的距离![]() ,
,![]()
![]()
当且仅当![]() 时等号成立,即
时等号成立,即![]() ,此时
,此时![]() ,
,
所以直线的方程为![]() 。
。