徐州市2005-2006学年度高三第一次质量检测
数学试题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分. 第Ⅰ卷1至2页. 第Ⅱ卷3至4页.考试结束后,将本试卷和答题卡一并收回.
第Ⅰ卷(选择题 共60分)
参考公式:
三角函数的和差化积公式
若事件A在一次试验中发生的概率是P,则它在n次独立重复试验中恰好发生k次的概率
一组数据
的方差
+
+…+
]
其中
为这组数据的平均数
一、 选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是符合题目要求的。
(1)集合P=
，则
等于
(A) 
(B) 
(C) 
(D)
(2)若θ是第一或第四象限角,则有
(A) 
(B) 
(C) 
(D) 
(3)直线
与直线
的夹角是
(A) 
(B) 
(C) 
(D)
(4)等差数列
中,若
,则
的值是
(A) 64 (B) 31 (C) 30 (D) 15
(5)若P: 
,Q: 
,则P 是Q的
(A)充分而不必要条件 (B) 必要而不充分条件
(C) 充要条件 (D) 即不充分也不必要条件
(6)过曲线
上的点P0的切线平行于直线
,则切点P0的坐标为
(A)(0,－1)或(1,0) (B) (1,0)或(－1, －4)
(C) (－1, －4)或(0,－2) (D) (1,0)或(2,8)
(7)函数
的图象相邻的两条对称轴之间的距离是
(A) 
(B) 
(C) 
(D)
(8) 设
,若
,则n的值为
(A) 7 (B) 11 (C) 15 (D) 16
(9)已知函数
的图象过点(－1, 3)和(1,1),若0<c<1,则实数a的取值范围是
(A) [2,3] (B) [1,3] (C)(1,2) (D) (1,3)
(10) 已知直线l:Ax+By+C=0(A、B不全为0)及两点P1（x1,y1）,P2（x2,y2）,若（Ax1+By1+C）（Ax2+By2+C）>0，且Ax1+By1+C> Ax2+By2+C,则
(A)直线l与直线P1P2不相交 (B) 直线l与线段P2 P1的延长线相交
(C) 直线l与线段P1 P2的延长线相交 (D) 直线l与线段P1P2相交
(11)已知A、B、C三点共线，O是这条直线外一点，设
且存在实数m，使
0成立，则点A分
的比为
(A) 
(B) 
(C) 
(D) 
(12)已知双曲线
的左、右焦点分别为F1、F2，点P在双曲线的右支上，若此双曲线的离心率为e，且PF1=ePF2，则e的最大值为
(A) 
(B) 
(C) 2 (D) 1
第Ⅱ卷(非选择题 共90分)
二、填空题：本大题共6小题,每小题4分,共24分.把答案填写在答题卡相应位置上.
(13)设直线
和圆直线
相交于两点A、B，则弦AB的垂直平分线方程为_________▲_________
(14)已知直线
，则直线
的值为_______▲_______
(15)某校有教师200人，男学生1200人，女学生1000人，现用分层抽样的方法从所有师生中抽取一个容量为n的样本，已知从女学生中抽取的人数为80人，则n的值为_____▲___
(16)从2005年12月10日零时起，徐州市电话号码由七位升到八位，若升位前与升位后0，1，9均不作为电话号码的首位，则扩容后增加了______▲_____个电话号码。
(17)若函数
的值域为R，则实数a的取值范围是_▲
(18)在等比数列中，
，且
，则使
的最大自然数n的值为_________▲_________
三、本大题共5小题，共66分。解答应写出文字说明、证明过程或演算步骤。
(19)（本小题满分12分，每小问满分4分）
某学生在军训时连续射击6次，每次击中的概率都是，且每次射击是否击中目标相互之间没有影响。求：
（Ⅰ）这名学生首次击中目标恰为第3次的概率；
（Ⅱ）这名学生在射击过程中，恰好有3次击中目标的概率；
（Ⅲ）这名学生在射击过程中，至少有1次击中目标的概率。
(20) （本小题满分12分，每小问满分6分）
在△ABC中，角A、B、C所对的边分别是a,b,c,又
。
（Ⅰ）求tanc的值；
（Ⅱ）若△ABC最短边的长为
，求△ABC的面积。
(21) （本小题满分14分，第一小问满分6分，第二小问满分8分）
已知函数
（Ⅰ）若函数
在区间（－∞，+∞）上为单调函数，求实数a的取值范围；
（Ⅱ）设A(x1,
)、B(x2, 
)是函数的两个极值点，若直线AB的斜率不小于
，求实数a的取值范围。
(22) （本小题满分14分，第一小问满分6分，第二小问满分8分）
已知向量n=(1,0),O是坐标原点，动点P满足：
比向量
在n上的投影多2。
（Ⅰ）求动点P的轨迹方程；
（Ⅱ）设B、C是点P的轨迹上不同的两点，满足
，在x轴上是否存在点A(m,0)，使得
?若存在，求出实数m的取值范围；若存在，说明理由。
(23) （本小题满分14分，第一小问满分2分，第二小问满分3分，第三小问满分9分）
已知函数
。
（Ⅰ）用a表示f(2)、f(3)并化简；
（Ⅱ）比较f(2)－2与f(1)－1，f(3)－3 与f(2)－2的大小关系，并由此归纳出一个更一般的结论（此结论不要求写出证明过程）；
（Ⅲ）比较
与
，
与的大小关系，并由此归纳出一个更一般的结论，并加以证明。
徐州市2005-2006学年度高三第一次质量检测
高三数学参考答案
一、选择题（每小题5分，共60分）
⑴D ⑵B ⑶A ⑷D ⑸A ⑹B ⑺C ⑻B ⑼C ⑽C ⑾A ⑿D
二、填空题（每小题4分，共24分）
⒀
⒁
⒂192 ⒃6.3×107 ⒄(0,1)∪
⒅8
三、解答题
(19)记“这名学生首次击中目标恰为第3次”为事件A1,这是一个相互独立事件，则
（Ⅰ）P(A1)=(1－)(1－)×=
.
…………………………………………………4分
（Ⅱ）记“这名学生在射击过程中，恰好有3次击中目标” 为事件A2，相当于做6次独立重复试验，则P(A2)=C
×
×(1－)3=
.…………………………………………8分
（Ⅲ）记“这名学生在射击过程中，至少有1次击中目标” 为事件A3,则
P(A3)=1－(1－)6=
答：这名学生首次击中目标恰为第3次的概率为；这名学生在射击过程中，恰好有3次击中目标的概率为；至少有1次击中目标的概率为.………………………12分
(20) （Ⅰ）因为
，所以B为锐角或钝角.
当B为钝角时，
，又
，
所以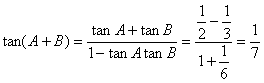
，
所以
,角C也是钝角，应舍去。…………………………………………3分
当B为锐角时，
，
又，同理
，所以
…………………………6分
（Ⅱ）由，0°<C<180°，所以C=135°，又tanA>tanB>0,
所以b边最短，即
，因为
，所以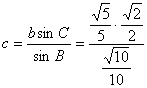
=1 …………………………………………10分
又，所以
所以△ABC的面积S=
…………………………12分
(21) （Ⅰ）因为函数在（－∞，+∞）上为单调递增函数，
所以
在（－∞，+∞）上恒成立。
由△=
，解得0<a<4 …………………………………………4分
又当a=0时，
（－∞，+∞）上为单调递增函数，
又当a=4时，
在（－∞，+∞）上为单调递增函数，所以0≤a≤4
…………………………………………6分
（Ⅱ）依题意，方程
=0有两个不同的实数根x1,、x2，
由△=
，解得a<0，或a>4,且x1＋x2=－a，x1x2= a …………………8分
所以
，
所以
=
. ………………………………12分
解之得－1≤a≤5, 所以实数a的取值范围是－1≤a<0,或4<a≤5. ……………14分
(22)(Ⅰ)设P点的坐标为(x,y),则
,
向量在n上的投影为
=(x,y) (1,0)= x ………………………………2分
所以
= x+2
………………………………4分
化简得
,所以动点P的轨迹方程是 .………………6分
(Ⅱ)若两点B、C满足
,得B、O、C三点共线，
设直线BC的方程为x=ky, B、C两点的坐标为（x1,y1）,（x2,y2）
由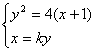
，得
=0
△=
，y1＋y2=4k，y1y2=－4 …………………………………………8分
又，所以
=0，即(x1－m)(x2－m)+ y1y2=0 ………………………10分
x1x2－m(x1＋x2)+m2+ y1y2=0,所以(k2+1) y1y2－mk( y1＋y2) +m2=0
化简得，（4m+4）k2= m2－4,当m=－1时不成立， ………………………12分
当m≠－1时，有
≥0，解之得
…………14分
（23）（Ⅰ）
………………………2分
（Ⅱ）
,
一般地,f(n+1) －(n+1)> f(n) －n(n∈N*) …………………………………………5分
(Ⅲ) 
所以
……………………………6分
判断
,证明如下:
(*)
因为
,
,所以(*)式显然成立,所以.…8分
一般地
(n∈N*)
…………………………………………9分
证明如下: 
>0
,此式显然成立,故(n∈N*)…………………14分