扬州市2005—2006学年高三第二次数学调研测试
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.
1、已知函数
的图象过（1，0），则
的反函数的图象一定过点（ ）
A．（1，2） B．（2，1） C．（0，2） D．（2，0）
2、设
，若区间
是函数
的单调递增区间，现将的图象按向量
的方向平移得到一个新的函数
的图象，则的一个单调递减区间可以是（ ）
A．
B．
C．
D．
3、定义在Ｒ上的周期函数
，其周期Ｔ＝２，直线
是它的图象的一条对称轴，且
上是减函数．如果Ａ、Ｂ是锐角三角形的两个内角，则（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
4、数列
是各项为正数的等比数列，
是等差数列，且
，则（ ）
A．
B．
C．
D．
与
的大小不确定。
5、对某种产品的5件不同正品和4件不同次品一一进行检测，直到区分出所有次品为止. 若所有次品恰好经过五次检测被全部发现，则这样的检测方法有（ ）
A．20种 B．96种 C．480种 D．600种
6、下列三图中的多边形均为正多边形，M、N是所在边上的中点，双曲线均以图中的F1、F2为焦点，设图①②③中的双曲线的离心率分别为e1、e2、e3，则 （ ）
 |
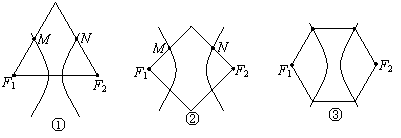A．e1＞e2＞e3 B．e1＜e2＜e3 C．e1=e3＜e2 D．e1=e3＞e2
7、在棱长为2R的无盖立方体容器内装满水，先将半径为R的球放入水中，然后再放入一个球，使它完全浸入水中，要使溢出的水量最大，则此球的半径是（ ）
A．
R B．
R C．
R D．
R
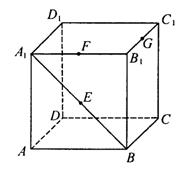8．如图所示，已知棱长为1的正方体容器
中，在
、
、
的中点E、F、G处各开有一个小孔，若此容器可以任意放置，则装水较多的容积是（小孔面积对容积的影响忽略不计）
（ ）
A．
B．
C．
D． 
9. 设A、B、C、D是半径为2的球面上四个不同的点，且AB·AC=0，AB·AD =0，AC·AD =0。△ABC、△ABD、△ACD的面积分别为S1、S2、S3，则S1+S2+S3最大值为（ ）
A．8 B.16 C.24 D.4
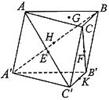10、如图，在三棱柱ABC—A′B′C′中，点E、F、H、 K分别为AC′、CB′、A′B、B′C′的中点，G为△ABC的重心. 从K、H、G、B′中取一点作为P， 使得该棱柱恰有2条棱与平面PEF平行，则P为 （ ）
A．K B．H C．G D．B′
11、身高互不相同的6个人排成2横行3纵列，在第一行的每个人都比他同列的身后的人个子矮，则所有不同排法的种数为 （ ）
A. 15 B. 84 C. 90 D. 540
12、过三棱柱任意两个顶点的直线共15条，其中异面直线有 （ ）
A．18对 B．24对 C．30对 D．36对
二、填空题：本大题共6小题，每小题4分，共24分。把答案填写在答题卡相应位置上。
13. 已知偶函数y=f(x)在区间[－1，0]上单调递增，且满足f(1－x)+f(1+x)=0，给出下列判断：
①f(5)=0； ②f(x)在[1，2]上是减函数； ③f(x)的图象关于直线x=1对称；
④f(x)在x=0处取得最大值； ⑤f(x)没有最小值。
其中正确的判断序号是_______________
14已知三棱锥
的三条侧棱
的长分别为
，且两两垂直，且满足
若三棱锥的体积取最大值时，侧面
与底面
成
，则三棱锥的体积取最大值时，
15.定义“等积数列”：在一个数列中，如果每一项与它的后一项的积都为同一常数，那么这个数列叫做“等积数列”，这个常数叫做该数列的公积.
(理)已知数列{an}是等积数列,且a1=2,公积为5,这个数列的前n项和Sn的计算公式为_______________________;
16． 对于各数互不相等的整数数组
(n是不小于2的正整数)，如果在
时有
，则称与是该数组的一个“逆序”，一个数组中所有“逆序”的个数称为该数组的“逆序数”。例如，数组(2,4,3,1)中有逆序“2,1”，“4,3”，“4,1”，“3,1”，其“逆序数”等于4。若各数互不相等的正整数数组
的“逆序数”是2，则
的“逆序数”是__________.
17.有6根细木棒,其中较长的两根分别为a, a,其余4根均为a,用它们搭成三棱锥,则其中两条较长的棱所在的直线所成的角的余弦值为 .
18．有一公用电话亭，在观察使用这个电话的人的流量时，设在某一个时刻，有n个人正在使用电话或等待使用的概率为
，且与时刻t无关，统计得到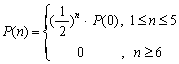
，那么在某一时刻这个公用电话亭里一个人也没有的概率P(0)的值是 ．
三、解答题：本大题共5小题，共66分。解答应写出文字说明、证明过程或演算步骤。
19 设定义在R上的函数f(x)满足:
① 对任意的实数x,y∈R,有f(x+y)=f(x)·f(y);
② 当x>0时,f(x)>1.
数列{an}满足a1=f(0),且f(an+1)=
(n∈N*).
(Ⅰ)求f(0),判断并证明函数f(x)的单调性;
(Ⅱ)求数列{an}的通项an的表达式;
(Ⅲ)令bn是最接近
,设Tn=
… +
.
20． 
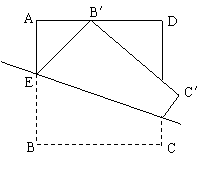如图，ABCD是边长为2的正方形纸片，沿某动直线l为折痕将正方形在其下方的部分向上翻折，使得每次翻折后点B都落在边AD上，记为B′；折痕l与AB交于点E，点M满足关系式
。
(1)建立适当的直角坐标系，求点M的轨迹方程；
(2)若曲线C是由点M的轨迹及其关于边AB对称的曲线组成的，F是AB边上的一点， = 4，过点F的直线交曲线C于P、Q两点，且→PF=λ→FQ，求实数λ的取值范围。
21.(本题12分)已知定义在区间(-m,m)(m＞0)上,值域为R的函数f(x)满足:①当0＜x＜m时,f(x)＞0;②对于定义域内任意的实数a、b均满足:f(a+b)=
.
(1)试求f(0);
(2)判断并证明函数f(x)的单调性；
（3）若函数f(x)存在反函数g(x)，当∈N时，
求证：g(
)+g(
)+…+g(
)＜g(
)
22．某地区发生流行性病毒感染，居住在该地区的居民必须服用一种药片预防，规定每人每天上午
时和晚上
时各服一片。现知该药片每片含药量为
毫克，若人的肾脏每
小时从体内滤出这种药的
，该药物在人体内的残留量超过
毫克，就将产生副作用。
（Ⅰ）某人上午时第一次服药，问到第二天上午时服完药后，这种药在他体内还残留多少？
（Ⅱ）若人长期服用这种药，这种药会不会对人体产生副作用？说明理由。（12分）
23．。已知x轴上有一列点P1，P2，P3，…，Pn，…，当
时，点Pn是把线段Pn－1 Pn+1作n等分的分点中最靠近Pn+1的点，设线段P1P2，P2P3，…，Pn Pn+1的长度分别为a1，a2，a3，…，an，其中a1=1.
（1）写出a2，a3和an（，
）的表达式；
（2）证明：a1+a2+a3+…+an<3（）；
（3）设点
在这些点中是否存在两个点同时在函数
的图象上，如果存在，请求出点的坐标；如果不存在，请说明理由.
参考答案
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.
1 A 2 D 3 A 4 B 5 D 6 D 7 C 8 A 9 A 10 C 11 C 12 D
二、填空题：本大题共6小题，每小题4分，共24分。把答案填写在答题卡相应位置上。
13 ①②④ 14 1
15 15.(理)Sn=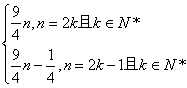
16 13 17 
18 .
三、解答题：本大题共5小题，共66分。解答应写出文字说明、证明过程或演算步骤。
19.解(Ⅰ)令y=0,x=1得:f(1)=f(1)·f(0)
f(1)(1-f(0))=0,
∵f(1)≠0, ∴f(0)=1
∵x>0时,f(x)>1
而由点到面①可知:1=f(0)=f(-x+x)=f (-x)·f(x)
∴f(x)=
∴x<0时,0<f(x)<1
∴x∈R时,0<f(x)
设x1<x2,由f(x2)=f[x1+(x2-x1)]=f(x1)·f(x2-x1)
而x1-x2>0,∴f(x2-x1)>1
∴f(x2)=f[x1+(x2-x1)]=f(x1)·f(x2-x1)>f(x1)
∴f(x)在R上是单调递增函数.
(Ⅱ)因为数列{an}满足a1=f(0)=1,且f(an+1)=
由(Ⅰ)可得f(an+1)=f(an+1)
即an+1=an+1
∴an+1-an=1(n∈N*)
∴an=n(n∈N*)
(Ⅱ)令bn=k(k∈N*)是最接近
的正整数,
则k-
由于k,n都是正整数 ∴k2-k+1≤n≤k2+k
所以满足bn=k的正整数n有k2+k-(k2-k+1)+1=2k个;
312<1000<322,322-32+1=993
T1000=
=
=
=64+
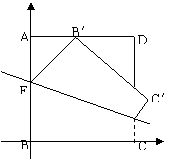20、（1）在BC所在的直线为x轴，以BA所在的直线为y轴，建立如图所示的直角坐标系。
设
，则
，从而直线
的斜率为
。 设
的中点为G，则
。
故直线的方程为：
，从而得点
，由得：
，所以：
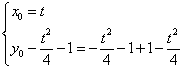，即：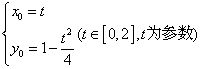
，消去t得：
即为点M的轨迹方程。
（2）由题意知：曲线C的方程为
，
。
设
与联立，得：
。
设
，则
① 
②
③
由①②③得：
，而
，所以
，故：
。
21.解：（1）令a=0,b=0,则有f(0)=
(2)令a=x,b=-x,得f(x)=f(-x)=0.所以函数f(x)为奇函数.
设任意的x1,x2,且0＜x1＜x2＜m,则m＞x2-x1＞0,∴f(x2-x1)＞0且f(x2)、f(x1) ＞0. ∴f(x2)-f(x1) =f(x2)+f(-x1)=f［x2+(-x1)］［1-f(x2)f(-x1)］
=f(x2-x1)［1+f(x2)f(x1)］＞0，
∴函数f(x)在区间(0,m)(m＞0)上单调递增.
又函数f(x)为奇函数且f(0)=0,因此函数f(x)在区间(-m,m)(m＞0)上单调递增.
(3)∵函数f(x)在区间(-m,m)( m＞0)上单调递增,∴函数f(x)必存在反函数g(x),且
g(x)也为奇函数, ∴函数g(x)在R上单调递增;且当x＞0时, m＞g(x)＞0.由f(a+b)=可得a+b=g［］,令f(a)=x,f(b)=y,则a=g(x),b=g(r),则上式可改写为:g(x)+g(y)=g(
)对任意的x,y∈R都成立
∴
∴
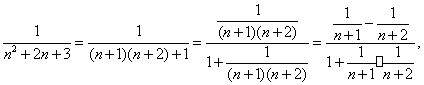
g()+g
［
］+［
］+…+［
］=
＜
.证毕.
22. 解：（Ⅰ）设人第
次服药后，药在体内的残留量为
毫克，则
，
，
，即到第二天上午时服完药后，这种药在他体内还残留
毫克； （6分）
（Ⅱ）由题意：
，∴
，
∴
是以
为首项，
为公比的等比数列，
∴
，（10分）
∵
，∴
，∴
。故若人长期服用这种药，这种药不会对人体产生副作用。（12分）
23、解：（1）由已知
令
令
同理：
所以
（2）因为
所以
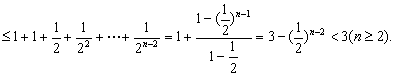
而
时，易知
成立，所以
（3）假设有两个点A（
、
，且
，
都在函数
上，即
所以
消去k得
，……①
以下考查数列
的增减情况，
，
当
时，
>0，所以对于数列
有
故，不可能存在p,q使得①式成立。因而，不存在。