导数的概念同步达纲练习
一、选择题
1．设函数f(x)在
处可导，则
等于（ ）
A．
B．
C．
D．
2．若
，则等于（ ）
A．
B．
C．3 D．2
3．若函数f(x)的导数为f′(x)=-sinx，则函数图像在点（4，f（4））处的切线的倾斜角为（ ）
A．90° B．0° C．锐角 D．钝角
4．一直线运动的物体，从时间t到t+△t时，物体的位移为△s，那么
为（ ）
A．从时间t到t+△t时，物体的平均速度
B．时间t时该物体的瞬时速度
C．当时间为△t 时该物体的速度
D．从时间t到t+△t时位移的平均变化率
5．对任意x，有
，f(1)=-1，则此函数为（ ）
A．
B．
C．
D．
6．设f(x)在处可导，下列式子中与相等的是（ ）
（1）
； （2）
；
（3）
（4）
。
A．（1）（2） B．（1）（3） C．（2）（3） D．（1）（2）（3）（4）
二、填空题
7．若函数f(x)在点处的导数存在，则它所对应的曲线在点
处的切线方程是_____________。
8．已知曲线
，则
_____________。
9．设
，则
_____________。
10．在抛物线
上依次取两点，它们的横坐标分别为
，
，若抛物线上过点P的切线与过这两点的割线平行，则P点的坐标为_____________。
三、解答题
11．曲线
在点A处的切线的斜率为3，求该曲线在A点处的切线方程。
12．在抛物线上求一点P，使过点P的切线和直线3x-y+1=0的夹角为
。
13．判断函数
在x=0处是否可导。
14．求经过点（2，0）且与曲线
相切的直线方程。
参考答案
同步达纲练习
一、选择题
1．C 2．B 3．C 4．B 5．B 6．B
二、填空题
7．
。
8．
。
9．-6。
10．（2，4）。
三、解答题
11．由导数定义求得
，
令
，则x=±1。
当x=1时，切点为（1，1），所以该曲线在（1，1）处的切线方程为y-1=3(x-1)即3x-y-2=0；
当x=-1时，则切点坐标为（-1，-1），所以该曲线在（-1，-1）处的切线方程为y+1=3(x+1)即3x-y+2=0。
12．由导数定义得f′(x)=2x，设曲线上P点的坐标为
，则该点处切线的斜率为
，根据夹角公式有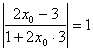
解得
或
，
由，得
；
由，得
；
则P（-1，1）或
。
13．
，
，
∵
，
∴
不存在。
∴函数f(x)在x=0处不可导。
14．可以验证点（2，0）不在曲线上，故设切点为
。
由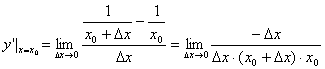
，
得所求直线方程为
。
由点（2，0）在直线上，得
，
再由在曲线上，得
，
联立可解得
，。所求直线方程为x+y-2=0。