数学归纳法及其应用举例单元练习（二）
一、选择题（本大题共6小题，每小题3分，共18分）
1.在应用数学归纳法证明凸n边形的对角线为
n(n－3)条时，第一步验证n等于
A. 1 B.2 C.3 D.0
2.等式12+22+32+…+n2=
A.n为任何自然数时都成立；B.仅当n=1，2，3时成立
C.n=4时成立，n=5时不成立；D.仅当n=4时不成立
3.用数学归纳法证明不等式
+…+
（n≥2,n∈N*)的过程中，由n=k逆推到n=k+1时的不等式左边
A. 增加了1项
； B.增加了“
”，又减少了“
”
C.增加了2项 D.增加了，减少了
4.用数学归纳法证明（n+1)(n+2)…(n+n)=2n·1·3·5·…（2n－1)(n∈N*)时，假设n=k时成立，若证n=k+1时也成立，两边同乘
A.2k+1 B.
C.
D.
5.证明1+
+…+
(n∈N*)，假设n=k时成立，当n=k+1时，左端增加的项数是
A. 1项 B.k－1项 C.k项 D.2k项
6.上一个n级台阶，若每步可上一级或两级,设上法总数为f(n),则下列猜想中正确的是
A.f(n)=n B.f(n)=f(n－1)+f(n－2)
C.f(n)=f(n－1)·f(n－2) D.f(n)=
二、填空题（本大题共5小题，每小题3分，共15分）
7.凸n边形内角和为f(k)，则凸k+1边形的内角和f(k+1)=f(k)+___________.
8.观察下列式子：1+
,1+
＜
,1+
,…则可归纳出：___________.
9.设f(n)=（1+
,用数学归纳法证明f(n)≥3.在“假设n=k时成立”后，f(k+1)与f(k)的关系是f(k+1)=f(k)·___________.
10.有以下四个命题：（1）2n＞2n+1(n≥3) (2)2+4+6+…+2n=n2+n+2(n≥1) (3)凸n边形内角和为f(n)=(n－1)π(n≥3) (4)凸n边形对角线条数f(n)=
(n≥4)．其中满足“假设n=k(k∈N,k≥n0).时命题成立，则当n=k+1时命题也成立.”但不满足“当n=n0（n0是题中给定的n的初始值）时命题成立”的命题序号是___________.
11.用数学归纳法证明
（a,b是非负实数，n∈N*)时，假设n=k命题成立之后，证明n=k+1命题也成立的关键是___________.
三、解答题（本大题共3小题，每小题9分，共27分）
12.已知an=
n∈N*求证：an＜1.
13.平面内有n个圆，其中任何两个圆都有两个交点，任何三个圆都没有共同的交点，试证明这n个圆把平面分成了n2－n+2个区域.
14.设f(k)是满足不等式log2x+log2(3·2k－1－x)≥2k－1(k∈N*)的正整数x的个数.
（1）求f(k)的解析式；
（2）记Sn=f(1)+f(2)+…+f(n),Pn=n2+n－1（n∈N*）试比较Sn与Pn的大小.
参考答案：
一、1.C 2.B 3.B 4.C 5.D 6.D 二、7.180°
8.1+
9.(1+
10.(2)（3） 11.两边同乘以
三、12.证明：(1)当n=1时，a1=＜1，不等式成立.
（2）假设n=k(k≥1)时，不等式成立，即ak=
＜1
亦即1+22+33+…+kk＜(k+1)k
当n=k+1时
ak+1=
=
=(
)k＜1.
∴n=k+1时，不等式也成立.
由（1）、（2）知,对一切n∈N*，不等式都成立.
13.证明：（1）当n=1时，一个圆把平面分成两个区域，而12－1+2=2，命题成立.
（2）假设n=k(k≥1)时，命题成立，即k个圆把平面分成k2－k+2个区域.
当n=k+1时，第k+1个圆与原有的k个圆有2k个交点，这些交点把第k+1个圆分成了2k段弧，而其中的每一段弧都把它所在的区域分成了两部分，因此增加了2k个区域，共有k2－k+2+2k=(k+1)2－(k+1)+2个区域.
∴n=k+1时，命题也成立.
由（1）、（2）知，对任意的n∈N*,命题都成立.
14.解：（1）∵log2x+log2(3·2k－1－x)≥2k－1
∴
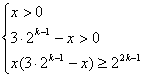,解得2k－1≤x≤2k,
∴f(k)=2k－2k－1+1=2k－1+1
(2)∵Sn=f(1)+f(2)+…+f(n)=1+2+22+…+2n－1+n=2n+n－1
∴Sn－Pn=2n－n2
n=1时,S1－P1=2－1=1＞0;n=2时，S2－P2=4－4=0
n=3时，S3－P3=8－9=－1＜0;n=4时，S4－P4=16－16=0
n=5时，S5－P5=32－25=7＞0;n=6时，S6－P6=64－36=28＞0
猜想，当n≥5时，Sn－Pn＞0
①当n=5时，由上可知Sn－Pn＞0
②假设n=k(k≥5)时，Sk－Pk＞0
当n=k+1时,Sk+1－Pk+1=2k+1－(k+1）2=2·2k－k2－2k－12(2k－k2)+k2－2k－1
=2(Sk－Pk)+k2－2k－1＞k2－2k－1=k(k－2)－1≥5(5－2)－1=14＞0
∴当n=k+1时，Sk+1－Pk+1＞0成立
由①、②可知，对n≥5，n∈N*，Sn－Pn＞0成立即Sn＞Pn成立
由上分析可知，当n=1或n≥5时，Sn＞Pn
当n=2或n=4时，Sn=Pn
当n=3时，Sn＜Pn. 