成都市2006届高中毕业班第一次诊断性检测题
数 学(文科)
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 得分 | |||||||||
注意事项:全卷满分为150分,完成时间为120分钟。
| 参考公式:如果事件A、B互斥,那么 | 球的表面积公式 |
| P(A+B)=P(A)+P(B) | S=4 |
| 如果事件A、B相互独立,那么 | 其中R表示球的半径 |
| P(A•B)=P(A)•P(B) | 球的体积公式 |
| 如果事件A在一次试验中发生的概率是P, 那么n次独立重复试验中恰好发生k次的概率 |
|
|
| 其中R表示球的半径 |
第Ⅰ卷(选择题,共60分)
一、选择题:本题共有12个小题,每小题5分;在每小题给出的四个选项中,只有一项是符合题目要求的,把正确选项的代号涂在机读卡的指定位置上。
1.lg8+3lg5的值为
(A) -3 (B) -1 (C) 1 (D) 3
2.若![]() ,则下列不等式中总成立的是
,则下列不等式中总成立的是
(A) ![]() (B)
(B)
![]()
(C) ![]() (D)
(D)
![]()
3.设![]() 或
或 ![]() 或
或![]() ,则
,则![]() 是
是![]() 的
的
(A) 充分但不必要条件 (B) 必要但不充分条件
(C) 充要条件 (D) 既不充分也不必要条件
4.已知![]() 是R上的增函数,若令
是R上的增函数,若令![]() ,则
,则![]() 是R上的
是R上的
(A) 增函数 (B) 减函数
(C) 先减后增的函数 (D) 先增后减的函数
5.已知直线l⊥平面α,直线m![]() 平面β,有下列四个命题:①
平面β,有下列四个命题:①![]()
②![]() ③
③![]() ④
④![]() 。其中真命题是
。其中真命题是
(A) ①② (B) ③④ (C) ②④ (D) ①③
6.将函数![]() 的图象按向量
的图象按向量![]() 平移后得到函数
平移后得到函数![]() 的图象,则向量
的图象,则向量![]() 可以是
可以是
(A) ![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D) ![]()
7.一组样本数据,容量为150。按从小到大的组序分成10个组,其频数如下表:
| 组号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 频数 | 15 | 17 | 14 | 18 | x | 13 | 19 | 16 | 12 | 11 |
那么,第5组的频率为
(A) 0.1 (B) 10 (C) 0.15 (D) 15
8.函数y=f (x)的图象如右图所示,则y =log0.2f (x)的示意图是
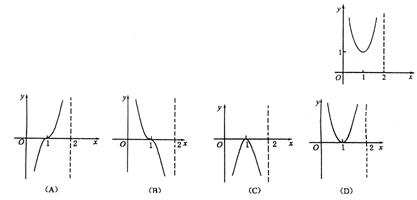
9.设向量![]() ,
,![]() ,若t是实数,且
,若t是实数,且![]() ,则
,则![]() 的最小值为
的最小值为
(A) ![]() (B)
1
(C)
(B)
1
(C) ![]() (D)
(D)
![]()
10.有A、B、C、D、E、F6个集装箱,准备用甲、乙、丙三辆卡车运送,每台卡车一次运两个。若卡车甲不能运A箱,卡车乙不能运B箱,此外无其它任何限制;要把这6个集装箱分配给这3台卡车运送,则不同的分配方案的种数为
(A) 168 (B) 84 (C) 56 (D) 42
11.已知![]() ,则
,则![]() =
=
(A)![]() (B)
(B) ![]() (C)
1 (D)
0
(C)
1 (D)
0
12.已知集合![]() 满足
满足![]() ,则p与q的关系为
,则p与q的关系为
(A) ![]() (B)
(B) ![]() (C)
(C)
![]() (D)
(D) ![]()
第Ⅱ卷 (非选择题,共90分)
| 得分 | 评卷人 |
二、填空题:(本大题共4小题,每小题4分,共16分)
把答案填在题中横线上。
13.![]() 的展开式中,x10的系数为
(用数字作答)。
的展开式中,x10的系数为
(用数字作答)。
 14.在数列
14.在数列![]() 和
和![]() 中,bn是an和an+1的等差中项,a1=2且对任意
中,bn是an和an+1的等差中项,a1=2且对任意![]() 都有
都有![]() ,则
,则![]() 的通项bn= 。
的通项bn= 。
15.若角![]() 、
、![]() 满足
满足![]() <
<![]() <
<![]() <
<![]() ,则
,则![]() 的取值范围是 。
的取值范围是 。
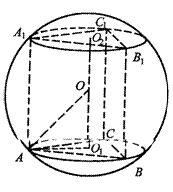
16.如图,棱长为3的正三棱柱内接于球O中,则球O的表面积为 。
三、解答题:(本大题共6小题,共74分)
解答应写出文字说明、证明过程或推演步骤。
| 得分 | 评卷人 |
17.(共12分)
甲、乙两人参加一项智力测试。已知在备选的10道题中,甲能答对其中的6道题,乙能答对其中的8道题。规定每位参赛者都从备选题中随机抽出3道题进行测试,至少答对2道题才算通过。
(I)求甲乙两人均通过测试的概率;
(II)求甲、乙两人至少有一人通过测试的概率。
| 得分 | 评卷人 |
18.(共11分)
已知ΔABC中,角A、B、C所对边分别是a、b、c,b<a<c且![]() 。求sin2A的值。
。求sin2A的值。
| 得分 | 评卷人 |
19.(共14分)
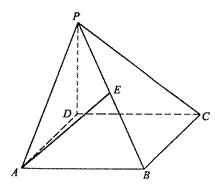 如图,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,且PD=AB=a,E是PB的中点。
如图,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,且PD=AB=a,E是PB的中点。
(I)求异面直线PD、AE所成的角;
(II)在平面PAD内求一点F,使得EF⊥平面PBC;
| 得分 | 评卷人 |
20.(共12分)
已知向量![]() 、t为正实数,
、t为正实数,![]() 。
。
(I)若![]() ,求k的最大值;
,求k的最大值;
(II)是否存在k、t使得![]() ?若存在,求出k的取值范围;若不存在,请说明理由。
?若存在,求出k的取值范围;若不存在,请说明理由。
| 得分 | 评卷人 |
21.(共12分)
某西部山区的某种特产由于运输的原因,长期只能在当地销售,当地政府对该项特产的销售投资收益为:每投入x万元,可获得利润![]() 万元。当地政府拟在新的十年发展规划中加快发展此特产的销售,其规划方案为:在规划前后对该项目每年都投入60万元的销售投资,在未来10年的前5年中,每年都从60万元中拨出30万元用于修建一条公路,5年修成,通车前该特产只能在当地销售;公路通车后的5年中,该特产既在本地销售,也在外地销售,在外地销售的投资收益为:每投入x万元,可获利润
万元。当地政府拟在新的十年发展规划中加快发展此特产的销售,其规划方案为:在规划前后对该项目每年都投入60万元的销售投资,在未来10年的前5年中,每年都从60万元中拨出30万元用于修建一条公路,5年修成,通车前该特产只能在当地销售;公路通车后的5年中,该特产既在本地销售,也在外地销售,在外地销售的投资收益为:每投入x万元,可获利润![]() 万元。问从10年的累积利润看,该规划方案是否可行?
万元。问从10年的累积利润看,该规划方案是否可行?
| 得分 | 评卷人 |
22.(共13分)
已知数列![]() 中,
中,![]() ,其前n项和为Sn,满足
,其前n项和为Sn,满足![]() ,
,![]() 且
且![]() 。数列
。数列![]() 的满足
的满足![]() 。
。
(I)求数列![]() 、
、![]() 的通项an与bn;
的通项an与bn;
(II)若![]() 记
记![]() 为数列
为数列![]() 的前n项和,求证:
的前n项和,求证:![]() 。
。
成都市2006届高中毕业班第一次诊断性检测题
数学试题(文科)参考答案及评人人分意见
第Ⅰ卷 (选择题,共60分)
一、选择题:(每小题5分,共60分)
1.原式=3lg2+3lg5=3lg10=3,选(D)。
2.由![]() ,选(C)或令特值:a=2,b=1,排除(A)、(D),再令
,选(C)或令特值:a=2,b=1,排除(A)、(D),再令![]() ,排除(B)。
,排除(B)。
3.![]() ;反之,
;反之,![]() 推不出q
推不出q![]()
![]() 推不出
推不出![]() 。选(A)
。选(A)
4.取![]() ,则
,则![]() 为减函数,选(B)。
为减函数,选(B)。
5.对②、④可画图举出反例,选(D)。
6.![]() ,由
,由![]() 的图象变为
的图象变为![]() 的图象,
的图象,![]() 选(B)。
选(B)。
7.![]() ,(选A)
,(选A)
8.![]() 是减函数,而
是减函数,而![]() 在(0,1)是减函数,在(1,2)是增函数,故
在(0,1)是减函数,在(1,2)是增函数,故![]() 在(0,1)是增函数,而在(1,2)应是减函数,选(C)。
在(0,1)是增函数,而在(1,2)应是减函数,选(C)。
9.![]()
![]() 选(C)。
选(C)。
10.分两类:①甲运B箱,有![]() 种;②甲不运B箱,有
种;②甲不运B箱,有![]() 。
。
![]() 不同的分配方案共有
不同的分配方案共有![]() +
+![]() =42(种),选(D)。
=42(种),选(D)。
11.![]() 。周期T=6。且
。周期T=6。且![]()
![]() ∴
∴![]()
![]()
![]() =
=![]() 。选(A)
。选(A)
12.![]() 。
。![]() 非空,
非空,![]() B非空。设
B非空。设![]() ,观察数轴,有
,观察数轴,有![]() 。即x=2是方程
。即x=2是方程![]() 的一个根,把
的一个根,把![]() 代入
代入![]() ,有
,有![]() 。选(D)。
。选(D)。
第Ⅱ卷 (非选择题,共90分)
二、填空题:(每小题4分,共16分)
13.设![]() 由
由![]() 。
。![]() 的系数为
的系数为![]() 。
。
14.![]() 。
。![]() 是公比为
是公比为![]() 的等比数列
的等比数列![]()
![]() 。
。
15.![]() 又
又
![]() 即
即![]() 。
。
[注]:只有左界者得1分。
16.可求得![]() 设该球的半径为R,则AO=R。由
设该球的半径为R,则AO=R。由![]() +
+
![]() ,得
,得![]() 。
。
三、解答题:(共74分)
17.解:(I)设甲、乙两人通过测试的事件分别为A、B,则
![]() ,
2分
,
2分
![]() 。
2分
。
2分
∵A、B相互独立,
∴甲、乙两人都通过测试的概率为
![]() 。
3分
。
3分
(II)∵A、B相互独立,
∴甲、乙两人都通过测试的概率为
![]() 。
3分
。
3分
∴甲、乙两人至少有一人通过测试的概率为
![]() 。
2分
。
2分
18.解:由![]() 有
有
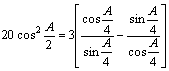 ,
2分
,
2分
即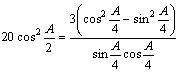 。
。
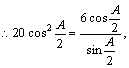 2分
2分
即![]() 。
。
![]() 。
1分
。
1分
∵A、B、C是三角形的内角,![]() ,
,
![]() 。
2分
。
2分
又∵b<a<c,∴A为锐角。
![]() 。
2分
。
2分
![]() 。
2分
。
2分
19.解:(I)建立如图所示的空间直角坐标系,则A (a,0,0) , B(a,a,0),
C(0,a,0),P(0,0,a)
![]() 。
。
![]()
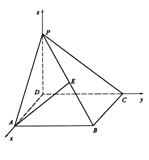
![]() 。
。
![]() 。
。
又![]()
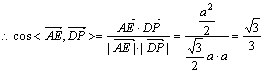 。
。
故异面直线AE、DP所成角为![]() 。
7分
。
7分
(II)∵F∈平面PAD,故设F(x,0,z),则有![]() 。
。
∵EF⊥平面PBC,∴![]() 且
且![]() 。
。
∴![]()
又![]() ,
,
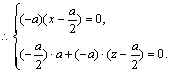
从而![]()
∴![]() ,取AD的中点即为F点。
7分
,取AD的中点即为F点。
7分
20.解:![]()
![]() 。
2分
。
2分
(I)若![]() 则
则![]() 。
。
![]() 。
2分
。
2分
整理,得![]()
![]() 3分
3分
(II)假设存在正实数k、t,使![]() ,则
,则
![]() 。
2分
。
2分
化简,得![]() 。
2分
。
2分
![]() 、t是正实数,故满足上式的k、t不存在。
、t是正实数,故满足上式的k、t不存在。
∴不存在这样的正实数k、t,使![]() 。
1分
。
1分
21.解:在实施规划前,由题设![]() (万元),知每年只须投入40万,即可获得最大利润100万元。
(万元),知每年只须投入40万,即可获得最大利润100万元。
则10年的总利润为W1=100×10=1000(万元)。 3分
实施规划后的前5年中,由题设![]() 知,每年投入30万元时,有最大利润
知,每年投入30万元时,有最大利润![]() (万元)。
(万元)。
前5年的利润和为![]() (万元)。
3分
(万元)。
3分
设在公路通车的后5年中,每年用x万元投资于本地的销售,而用剩下的(60-x)万元于外地区的销售投资,则其总利润为
![]()
![]() 。
3分
。
3分
当x=30时,W2max=4950(万元)。
从而10年的总利润为![]() (万元)。
2分
(万元)。
2分
![]() ,故该规划方案有极大实施价值。
1分
,故该规划方案有极大实施价值。
1分
22.解:(I)n=1时,![]() 由
由![]() 。
1分
。
1分
当n≥2时
![]() ①
①
![]() ②
②
由②—①,有![]() 2分
2分
从而,![]() 。
。
∴数列![]() 是以1为首项,
是以1为首项,![]() 为公比的等比数列。
为公比的等比数列。
∴![]() 。
3分
。
3分
∴ ![]() 1分
1分
(II)当![]() 时,
时,![]() 。
1分
。
1分
![]() 。
。
∵![]() ③
③
![]() 。
④
。
④
由③—④,得![]()
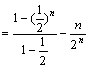 2分
2分
![]()
![]() 。
。
![]() 。
1分
。
1分
![]()
![]() 。
1分
。
1分