四川省广安实验中学高三年级阶段测试
数学（理科）试题
一、选择题：（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一个是符合题目要求的）
1．已知
为三角形的一个内角，且
=表示（ ）
A．焦点在x轴上的椭圆 B．焦在点y轴上的椭圆
C．焦点在x轴上的双曲线 D．焦点在y轴上的双曲线
2．双曲线
两焦点为F1，F2，点P在双曲线上，直线PF1，PF2倾斜角之差为
则△PF1F2面积为 （ ）
A．16
B．32 C．32 D．42
3．要使直线
与焦点在x轴上的椭圆
总有公共点，实数a的取
值范围是 （ ）
A．
B．
C．
D．
4．与双曲线有共同渐近线，且过
的双曲线的一个焦点到一条渐近
线的距离是 （ ）
A．
B．
C．
D．
5．过点M（－2，0）的直线m与椭圆
交于P1，P2，线段P1P2的中点为P，设直线m的斜率为k1（
），直线OP的斜率为k2，则k1k2的值为 （ ）
A．2 B．－2 C．
D．－
6．设
为单元素集，则t值的个数是 （ ）
A．1 B．2 C．3 D．4
7．a、b是两条异面直线，下列结论正确的是 （ ）
A．过不在a、b上的任一点，可作一个平面与a、b都平行
B．过不在a、b上的任一点，可作一条直线与a、b都相交
C．过不在a、b上的任一点，可作一条直线与a、b都平行
D．过a可以且只可以作一个平面与b平行
8．已知点F1、F2分别是双曲线
的左、右焦点，过F1且垂直于x轴的直线与双曲线交于A、B两点，若△ABF2为锐角三角形，则该双曲线的离心率e的范围是（ ）
A．
B．
C．
D．
9．过抛物线
的焦点F的直线m的倾斜角
交抛物线于A、B两点，且A点在x轴上方，则FA的取值范围是 （ ）
A．
B．
C．
D．
10．在正方体ABCD—A1B1C1D1中，O为AC、BD的交点，则C1O与A1D所成的角为（ ）
A．60° B．90° C．
D．
11．直平行六面体ABCD—A1B1C1D1的棱长均为2，
，则对角线A1C与侧面DCC1D1所成角的正弦值为 （ ）
A． B．
C．
D．
12．正方体ABCD—A1B1C1D1中，P在侧面BCC1B1及其边界上运动，且总保持AP⊥BD1，则动点P的轨迹是 （ ）
A．线段B1C B．线段BC1
C．BB1中点与CC1中点连成的线段 D．BC中点与B1C1中点连成的线段
二、填空题（本大题共4小题，每小题4分，共16分）
13．在棱长为1的正方体ABCD—A1B1C1D1中，O为正方形ABCD的中心，E、F分别为AB、BC的中点，则异面直线C1O与EF的距离为 .
14．已知抛物线
上两点
关于直线
对称，且
，那么m的值为
.
15．从双曲线上任意一点P引实轴平行线交两渐近线于Q、R两点，则PQPR之值为
.
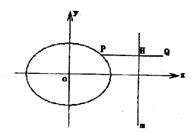
16．过抛物线
焦点F的直线与抛物线交于P、Q，由P、Q分别引其准线的垂线PH1、QH2垂足分别为H1、H2，H1H2的中点为M，记PF=a，QF=b，则MF=
。
三、解答题（本大题共6小题，第17—21小题各12分，第22小题14分，共74分，解答应有证明或演算步骤）
17．解不等式：
.
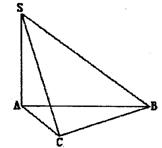
18．在三棱锥S—ABC中，∠SAB=∠SAC=∠ACB=90°，AC=2，BC=
，SB=
|
（2）求侧面SBC与底面ABC所成二面角大小；
（3）求异面直线SC与AB所成角的大小.
（用反三角函数表示）
19．点B（－1，0）为抛物线
上的定点，P、Q为动点，且在抛物线上，
当BP⊥PQ时，求点Q横坐标的取值范围.
20．已知
，
（1）求点P（x，y）的轨迹C的方程；
（2）若直线
与曲线C交于A、B两点，已知点D（0，－1）
且有AD=BD，试求t的取值范围.
|
上任一点P，作E的右准线m的垂线PH（H为垂足），
延长PH到Q，使HQ=λPH（λ>0）.
（1）求当P在E上运动时，点Q的轨迹G的方程.
（2）若轨迹G是与椭圆E离心率相等的椭圆，求λ的值.
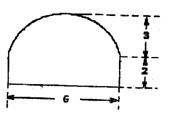
22．如图，一条隧道横截面由一段抛物线及矩形的三边围成，各段长度见图中所示（单位：米）某卡车空载时能通过此隧道.
（1）现有一集装箱，箱宽3米，装上卡车后，箱顶高4.5米，问此车能否通过这条隧道？
（2）若卡车载货板离地面1.4米,为安全起见，集装箱顶与隧道顶部距离不少于0.1米，在可以通过隧道的情况下，长、宽各为多少米的集装箱截面积最大？
|
参考答案（理）
一、选择题：（本大题共12小题，每小题5分，共60分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | A | C | C | D | D | D | B | A | D | D | A |
二、填空题（本大题共12小题，每小题5分，共60分）
13． 14．
15．
16．
三、解答题：（本大题共6小题，第17—21小题各12分，第22小题14分，共74分）
17．
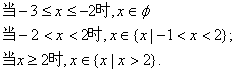
18．（1）
∵BC
平面ABC； ∴SA⊥BC ∵AC⊥BC ∴BC⊥平面ACS
∵SC平面ACS ∴BC⊥SC.
（2）∵面SBC∩面ABC=BC； SC⊥BC于C，AC⊥BC于C；
∴∠SCA为所求二面角的平面角 又∵SB=
BC=
∴SC=4 ∵AC=2 ∴∠SCA=60°
（3）
19．解：
易见
；
当
20．解：（1）
（2）
21．解：（1）设Q（x, y），相应点P（x0, y0）, H（3,y0），
∵HQ=λPH即QH=λHP； ∴点H分有向线段QP所成比为λ，
（2）
; 
22．（1）不能
（2）
.