四川省重点中学高2006级数学能力题训练二
（由四川教科院组织名校教师联合编写）
1. 已知数列
，那么“对任意的
，点
都在直线
上”是“为等差数列”的 （ ）
(A)必要而不充分条件 (B)充分而不必要条件
(C)充要条件 (D)既不充分也不必要条件
2. 已知函数f(x)定义域为R，则下列命题：
①y=f(x)为偶函数，则y=f(x+2)的图象关于y轴对称.
②y=f(x+2)为偶函数，则y=f(x)关于直线x=2对称.
③若函数f(2x+1)是偶函数，则f(2x)的图象关于直线 
对称.
④若f(x-2)=f(2-x)，则y=f(x)关于直线x=2对称.
⑤y=f(x-2)和y=f(2-x)的图象关于x=2对称.
其中正确的命题序号是( )
A、①②④ B、①③④ C、②③⑤ D、②③④
3. 一间民房的屋顶有如图三种不同的盖法：①单向倾斜；②双向倾斜；③四向倾斜，记三种盖法屋顶面积分别为P1、P2、P3．
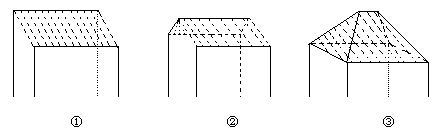
若屋顶斜面与水平面所成的角都是α，则
[ ]
A．P3＞P2＞P1 B．P3＞P2=P1
C．P3=P2＞P1 D．P3=P2=P1
4. 已知关于x的方程
没有实数解,则实数m的取值范围是
(A)
(B) 
(C) 或 
(D)
5. xy>0是x+y=x+y的 （ ）
A．充分不必要条件 B．必要不充分条件 C．充要条件 D．不充分不必要条件
6. 给定实数
，定义
为不大于的最大整数，则下列结论不正确的是
A．
B．
C．
是周期函数 D．是偶函数
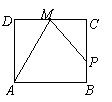
7. 如图，点P在边长为1的正方形ABCD边上运动，设点M是CD边的中点，点P沿A®B®C®M运动时，点Ｐ经过的路程记为x，△APM的面积为y，则函数y=f(x)的图象只可能是（ ）.
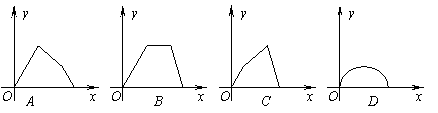
8. 方程
有五个不相等的实数根，则这五根之和为（ ）.
| A、5 | B、10 | C、 | D、 |
9. 方程
有一个负根且无正根，则
的取值范围是
（ ）
≤
≥
10. 
≤
的解集是
，则的取值范围是
（ ）
11. 设
、
分别是定义在R上的奇函数和偶函数，当
,
且
，则不等式
的解集是 （ ）
A．
B．
C．
D．
12. 设函数
区间
，
则使M=N成立的实数对（a，b），有 （ ）
A．0个 B．1个 C．2个 D．无数多个
13. 已知二次函数f（x）= x2－3x + p－1，若在区间[0，1]内至少存在一个实数c，
使f（c）＞0，则实数p的取值范围是_____________.
14. 已知函数
.给出下列命题：①f(x)必是偶函数；②f(0)= f(2)时，f(x)的图象必关于直线x=1对称；③若
，则f(x)在区间
上是增函数；
④f(x)有最小值
.
其中正确命题的序号是 .
15. 若直线y=2a与函数y=ax-1(a>0,且a≠1)的图象有两个公共点，则a的取值范围是_______.
16. 设坐标平面内有一个质点从原点出发，沿x轴跳动，每次向正方向或负方向跳1个单位，经过5次跳动质点落在点（3，0）（允许重复过此点）处，则质点不同的运动方法共有________种（用数字作答）。
17. 已知函数
的定义域为
，值域为
．试求函数
（
）的最小正周期和最值
18.甲、乙两人进行五次比赛，如果甲或乙无论谁胜了三次，比赛宣告结束。假定甲获胜的概率是
，乙获胜的概率是
，试求下列概率。
（I）比赛以甲3胜1败而结束的概率；
（II）比赛以乙3胜2败而结束的概率；
（III）设甲先胜3次的概率为a，乙先胜3次的概率为b，求a:b的值。
19. 已知函数：
．
（1）证明：f(x)+2+f(2a－x)=0对定义域内的所有x都成立；
（2）当f(x)的定义域为[a+
,a+1]时，求证：f(x)的值域为[－3，－2]；
（3）设函数g(x)=x2+(x－a)f(x) ,求g(x) 的最小值 ．
20. 已知集合
，试问集合A与B共有几个相同的元素，并写出由这些“相同元素”组成的集合.
21. 设关于x的一元二次方程2x2－ax－2=0的两根的α、β(α<β)，函数f(x)＝
⑴求f(α)·f(β)的值；
⑵证明f(x)是[α,β]的增函数；
（3）当a为何值时，f(x)在区间[α,β]上的最大值与最小值之差最小？
22. 已知点
都在直线
上，
为直线
与轴的交点，数列
成等差数列，公差为1. （
）
(1)求数列，
的通项公式；
(2)若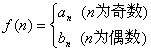
， 问是否存在
，使得
成立；若存在，求出
的值，若不存在，说明理由.
(3)求证：
…… +
(
2, )
高三数学能力训练2参考答案
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| B | C | D | C | A | A | A | C | D | A | D | A |
13. （1，+∞）
14.③
15. 
16.5
17. 解： 
……2’
…………………………4’
当
＞0时，
，
解得
，………………………………………………………………6’
从而，
，
T=
，最大值为5，最小值为－5；………………………………………………8’
当m＜0时， 解得
，………………………………………………10’
从而，
，T=，最大值为
，
最小值为
．……………………………………………………………………12
18. 解：（I）以甲3胜1败而结束比赛，甲只能在1、2、3次中失败1次，因此所求概率为：
（II）乙3胜2败的场合
，因而所求概率为：
（III）甲先胜3次的情况有3种：3胜无败，3胜1败，3胜2败
其概率分别为
于是
乙获胜概率
19. 解（1）证明：
．
∴结论成立 ………………………………………………………………………………4’
（2）证明：
当
，
，
，
，
∴
．
即
．………………………………………………………………8’
（3）
①当
．
如果
即
时，则函数在
上单调递增，
∴
．
如果
．
当
时，
最小值不存在．……………………………………………………10’
②当
，
如果
．
如果
．
当
．
．……………………………………………12’
综合得：当
时， g（x）最小值是
；当
时， g（x）最小值是
；当
时， g（x）最小值为
；当时， g（x）最小值不存在．
20. 解：因为
，所以
，
因为
，所以
，
所以A、B有两个公共元素，由这些“相同元素”组成的集合是{1，9}.
21. 解：⑴ f(α)f(β)＝－4
⑵设α≤x1<x2≤β，f(x1)－f(x2)＝
又∵2x12-ax1-2≤0, 2x22-ax2-2≤0,∴a(x1+x2)+4≥2(x12+x22) 得4+a(x1+x2)－4x1x2≥2(x12+x22) －4x1x 2=2(x1-x2)2>0，得f(x1)<f(x2)∴f(x)在[α,β]为增函数．
⑶由⑴⑵可知，f(x)max=f(β)>0，f(x)min＝f(α)<0
∵f(α)·f(β)＝4，而f(β)－f(α)＝f(β)+f(α)≥4
符号在f(B)＝2时成立，即
22. 
解 (1) 
(2) 
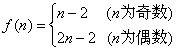
假设存在符合条件的
(ⅰ)若为偶数，则
为奇数，有
如果
，则
与为偶数矛盾.不符舍去；
(ⅱ) 若为奇数，则为偶数，有
这样的也不存在.
综上所述：不存在符合条件的.
(3) 
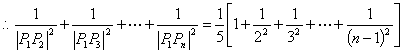
