四川省重点中学高2006级数学能力题训练六
（由四川教科院组织名校教师联合编写）
1.
天文台用3.2万元买一台观测仪，已知这台观测仪从启用的第一天起连续使用，第n天的维修保养费为
元（n∈N*），使用它直至报废最合算（所谓报废最合算是指使用的这台仪器的平均耗资最少）为止，一共使用了
（ ）
A．800天 B．1000天 C．1200天 D．1400天
2.
两个正数a、b的等差中项是5，等比中项是4。若a＞b，则双曲线
的离心率e等于
（ ）
A．
B．
C．
D．
3. 有一棱长为a的正方体框架，其内放置一气球，是其充气且尽可能地膨胀（仍保持为球的形状），则气球表面积的最大值为 （ ）
A．
B．2 C．3 D．4
4. 直角坐标xOy平面上，平行直线x＝n（n＝0，1，2，……，5）与平行直线y＝n（n＝0，
1，2，……，5）组成的图形中，矩形共有 （ ）
A．25个 B．36个 C．100个 D．225个
5.
方程
所对应的曲线图形是 （ ）
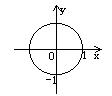
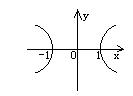
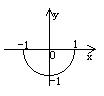
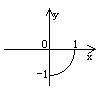
A． B． C． D．
6.
设0＜x＜π，则函数
的最小值是
（ ）
A．3 B．2
C． D．2-
7.
四面体
的六条棱中，其中五条棱的长度都是2，则第六条棱长的取值范围是( )
A．
B．
C．
D．
8.
若直线
与曲线
有两个不同的交点，则
的取值范围是 （ ）
A．
B．
C．
D．
或
9. 某企业购置了一批设备投入生产，据分析每台设备生产的总利
润
（单位：万元）与年数
满足如图的二次函数关系。
要使生产的年平均利润最大，则每台设备应使用 （ ）
A．3年 B．4年 C．5年 D．6年
10.
从长度分别为1，2，3，4的四条线段中，任取三条的不同取法共有n种，在这些取法中，以取出的三条线段为边可组成的三角形的个数为m，则
等于 （ ）
A. 0 B．
C．
D．
11. 设函数
，则
的值为 （ ）
A．a B．b
C．a、b中较小的数 D．a、b中较大的数
12. 已知点P在定圆O的圆内或圆周上，圆C经过点P且与定圆O相切，则动圆C的圆心轨迹是 （ ）
A．圆或椭圆或双曲线 B．两条射线或圆或抛物线
C．两条射线或圆或椭圆 D．椭圆或双曲线和抛物线
13.
有四个好友A, B, C, D经常通电话交流信息, 已知在通了三次电话后这四人都获悉某一条高考信息, 那么第一个电话是A打的情形共有 种.甲、乙、丙、丁、戊5名学生进行投篮比赛，决出了第1至第5名的不同名次，甲、乙两人向裁判询问成绩，根据右图所示裁判的回答，5人的名次排列共有
种不同的情况.
14. x0是x的方程ax=logax(0<a<1)的解，则x0,1,a这三个数的大小关系是
15.
已知矩形
的边
平面
现有以下五个数据：
当在
边上存在点
，使
时，则
可以取_____________.（填上一个正确的数据序号即可）
16. 某池塘中野生水葫芦的面积与时间的函数关系的图象，如右图所示. 假设其关系为指数函数，并给出下列说法
①此指数函数的底数为2；
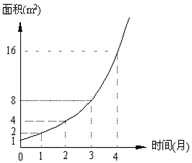②在第5个月时，野生水葫芦的面积就会超过30m2；
③野生水葫芦从4m2蔓延到12m2只需1.5个月；
④设野生水葫芦蔓延到2m2,3m2, 6m2所需的时间分别
为t1, t2, t3, 则有t1 + t2 = t3；
⑤野生水葫芦在第1到第3个月之间蔓延的平均速度
等于在第2到第4个月之间蔓延的平均速度.
其中正确的说法有 . (请把正确说法的序号都填在横线上)
17. 一个口袋内有4个不同的红球，6个不同的白球，
（1）从中任取4个球，红球的个数不比白球少的取法有多少种？
（2）若取一个红球记2分，取一个白球记1分，从中任取5个球，使总分不少于7分的
取法有多少种？
18. 摸球兑奖，口袋中装有4红4白共8个小球，其大小和手感都无区
别，交4元钱摸4个球，具体奖金如下：4红(10元)、3红(5元)、2红(1元)、1红(1包
0.2元的葵花籽)，试解释其中的奥秘
19. 已知
的展开式中含xn项的
系数相等，求实数m的取值范围
20. 已知10件产品中有3件是次品.
（1）任意取出3件产品作检验，求其中至少有1件是次品的概率；
（2）为了保证使3件次品全部检验出的概率超过0.6，最少应抽取几件产品作检验？
21.
平面上两个质点A、B 分别位于（0，0），（2，2），在某一时刻同时开始，每隔1秒钟向上下左右任一方向移动1个单位，已知质点A向左右移动的概率都是
向上下移动的概率分别是
和
质点B向各个方向移动的概率是
求：（1）4秒钟后A到达C（1，1）的概率；
（2）三秒钟后，A，B同时到达D（1，2）的概率
22. （文）如图甲、乙连接的6个元件,它们断电的概率第一个为P1=0.6,第二个为P2=0.2,其余四个都为P=0.3.分别求甲断电、乙通电的概率.
 |
（理）已知a＞1，数列
的通项公式是
，前n项和记作
（n＝1，2，…），规定
．函数
在
处和每个区间（
，
）（i＝0，1，2，…）上有定义，且
，
（i＝1，2，…）．当
（，
）时，f（x）的图像完全落在连结点
（，
）与点
（，
）的线段上．
（Ⅰ）求f（x）的定义域；
（Ⅱ）设f（x）的图像与坐标轴及直线l：
（n＝1，2，…）围成的图形面积为
，
求及
；
（Ⅲ）若存在正整数n，使得
，求a的取值范围．
高三数学能力训练6参考答案
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| A | C | B | D | D | C | B | A | C | B | C | C |
13. 16 54。 14.10或10
15.①或② 16. ①②③
17.解（1）将取出4个球分成三类情况1）取4个红球，没有白球，有
种 2）取3个红球1个白球，有
种；3）取2个红球2个白球，有
14. 解：摸出4球有C84＝70种可能性，四“红”只有一种，三“红”：C43C41＝16种，2“红”：C42C42＝36种.1“红”：C41C43＝16种 共计：赌70次收参赌费280元，平均奖金1×10+16×5+36×1+16×0.2＝129.2(元).所以，每赌70次，该赌者可净赚150.8元
15. m
16. 解：（1）任意取出3件产品作检验，全部是正品的概率为
…………3分
至少有一件是次品的概率为
……………………6分
（2）设抽取n件产品作检验，则3件次品全部检验出的概率为
………8分
由
整理得：
，……………………10分
∴当n=9或n=10时上式成立.…………11分
答：任意取出3件产品作检验，其中至少有1件是次品的概率为
为了保证使3件次品全部检验出的概率超过0.6，最少应抽取9件产品作检验.………………12分
17.
18. （文）解：图甲：AB、CD、EF三线路断电事件为M、N、G,每个线路断电二个元件至少有一个断电,且它们是相互独立的,于是：
P（M）=1－（1－0.6）（1－0.2）=1－0.4×0.8=0.68
P（N）=P（G）=1－（1－0.3）（1－0.3）=1－0.7×0.7=0.51
由于事件M、N、G相互独立,所以电器断电的概率P（M·N·G）=0.68×0.51×0.51=0.177.
图乙：1、3、5通路的概率P1=1-0.6×0.3×0.3=0.946；
2、4、6通路的概率P2=1-0.2×0.3×0.3=0.982；
所以图乙通路的概率= P1×P2=0.946×0.982=0.929。
（理）解：（1）f（x）的定义域是
，
由于所有的
都是正数，故是单调递增的．
∵
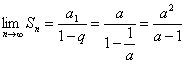∴f（x）的定义域是
（Ⅱ）∵ 
（i＝1，2，…）与i无关．
∴ 所有的
，
，
…共线，
该直线过点（a，a），斜率为1-a， ∴ 
．
当n≥2时，是一个三角形与一个梯形面积之和（如上图所示）．梯形面积是
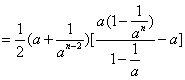
于是
故
（Ⅲ）解法一：结合图像，易见
即a≥2时，
，
而
，即a＜2时，
故当1＜a＜2时，存在正整数n，使得
解法二：假设存在正整数n，使得，
则应有
∵ 
， ∴ 
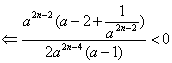
∴ 1＜a＜2时，存在正整数n，使得
成立