四川省重点中学高2006级数学能力题训练三
(由四川教科院组织名校教师联合编写)
1.
已知实数a、b、c满足b+c=6-4a+3![]() ,c-b=4-4a+
,c-b=4-4a+![]() ,则a、b、c的大小关系是
( )
,则a、b、c的大小关系是
( )
A.c≥b>a B.a>c≥b C.c>b>a D.a>c>b
2.
设实数x,
y满足x + y=4, 则![]() 的最小值为 ( )
的最小值为 ( )
A. ![]() B.4 C.2
B.4 C.2![]() D.8
D.8
3. 对“a、b、c是不全相等的正数”,给出下列判断:
①(a-b)2+(b-c)2+(c-a)2≠0; ②a>b与a<b及a≠c中至少有一个成立;
③a≠c,b≠c,a≠b不能同时成立.
其中判断正确的个数为 ( )
A.0个 B.1个 C.2个 D.3个
4.
定义在R上的函数y=f(x),在(-∞,![]() )上是增函数,且函数 y=f(x+
)上是增函数,且函数 y=f(x+![]() )是偶函数,当x1<
)是偶函数,当x1<![]() ,x2>
,x2>![]() 且
且![]() 时,有
( )
时,有
( )
A.f(2![]() -x1)> f(2
-x1)> f(2![]() -x2) B.f(2
-x2) B.f(2![]() -x1)= f(2
-x1)= f(2![]() -x2)
-x2)
C.f(2![]() -x1)< f(2
-x1)< f(2![]() -x2) D.-f(2
-x2) D.-f(2![]() -x1)< f(x2-2
-x1)< f(x2-2![]() )
)
5.
已知a![]() b,且a
b,且a![]() sin
sin![]() +acos
+acos![]() -
-![]() =0 ,b
=0 ,b![]() sin
sin![]() +bcos
+bcos![]() -
-![]() =0,则连接(a,a
=0,则连接(a,a![]() ),
),
(b,b![]() )两点的直线与单位圆的位置关系是
( )
)两点的直线与单位圆的位置关系是
( )
A.相交 B.相切 C.相离 D.不能确定
6.
M(![]() 为圆
为圆![]() 内异于圆心的一点,则直线
内异于圆心的一点,则直线![]() 与该圆的位置关系为 ( )
与该圆的位置关系为 ( )
A.相切 B.相交 C.相离 D.相切或相交
7.
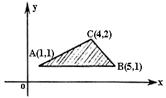 在如图所示的坐标平面的可行域(阴影部分且包括边界)内,目标函数
在如图所示的坐标平面的可行域(阴影部分且包括边界)内,目标函数![]() 取得最大值的最优解有无数个,则a为
( )
取得最大值的最优解有无数个,则a为
( )
A.-2 B.2 C.-6 D.6
8. 设△ABC的一个顶点是A(3,-1),∠B,∠C的平分线方程分别是x=0,y=x,则直线BC的方程是 ( )
A.y=2x+5 B.y=2x+3 C.y=3x+5 D.![]()
9. 三边均为整数且最大边的长为11的三角形的个数为 ( )
A.15 B.30 C.36 D.72
10.
若关于![]() 的方程
的方程![]() 有且只有两个不同的实数根,则实数
有且只有两个不同的实数根,则实数![]() 的取值范围是
( )
的取值范围是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11. 已知A(-1,0),B(1,0),点C(x,y)满足:![]() ,则
,则![]() ( )
( )
A.6 B.4 C.2 D.不能确定
12.
抛物线![]() 与直线
与直线![]() 交于A、B两点,其中点A的坐标为(1,2),设抛物线的焦点为F,则FA+FB等于 ( )
交于A、B两点,其中点A的坐标为(1,2),设抛物线的焦点为F,则FA+FB等于 ( )
A.7 B.![]() C.6 D.5
C.6 D.5
13. 黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案:
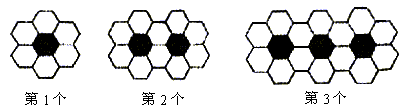
 则第n个图案中有白色地面砖____________块.
则第n个图案中有白色地面砖____________块.
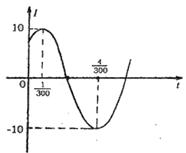
14. 电流强度I(安)随时间t(秒)变化的函数
I=![]() 的图象如图
的图象如图
所示,则当![]() 秒时,电流强度是
安
秒时,电流强度是
安
15. 已知点![]() 是函数
是函数![]() 上的两个不同点,且
上的两个不同点,且![]() ,试根据图像特征判定下列四个不等式的正确性:①
,试根据图像特征判定下列四个不等式的正确性:①![]() ;②
;②![]() ;③
;③![]()
![]() ;④
;④![]() 。其中正确不等式的序号是
.
。其中正确不等式的序号是
.
16.
已知集合A={(x,y)|![]() =2,x、y∈R},B={(x,y)|4x+ay=16,x、y∈R},若A∩B=
=2,x、y∈R},B={(x,y)|4x+ay=16,x、y∈R},若A∩B=![]() ,则实数a的值为
.
,则实数a的值为
.
17. 已知函数f(x)=sin(wx+j),xÎR,(其中w>0)的图象与x轴在原点右侧的第一个交点为N(6,0),又f(2+x)=f(2-x),f(0)<0,求这个函数的解析式.
18.
已知△ABC的周长为6,![]() 成等比数列,求(1)△ABC的面积S的最大值; (2)
成等比数列,求(1)△ABC的面积S的最大值; (2)![]() 的取值范围.
的取值范围.
19.
已知![]() 为
为![]() 的三个内角,
的三个内角,
且![]() .
.
(1)当![]() 取得最小值时,求
取得最小值时,求![]() 的度数;
的度数;
(2)当![]() 时,将函数
时,将函数![]() 按向量
按向量![]() 平移后得到函数
平移后得到函数![]() ,
,
求向量![]()
20. 已知向量![]() .①若点A、B、C能构成三角形,求实数m应满足的条件;②若△ABC为直角三角形,且∠A为直角,求实数m的值
.①若点A、B、C能构成三角形,求实数m应满足的条件;②若△ABC为直角三角形,且∠A为直角,求实数m的值
21. 已知集合![]() ,集合
,集合![]() ,求集合
,求集合![]()
22.
ABC的三个内角A、B、C的对边的长分别为a、b、c,有下列两个条件:(1)a、b、c成等差数列;(2)a、b、c成等比数列.现给出三个结论:(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
请你选取给定的两个条件中的一个条件为条件,三个结论中的两个为结论,组建一个你认为正确的命题,并证明之.
高三数学能力训练3参考答案
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| A | C | C | A | A | C | A | A | C | D | B | A |
13. ![]()
14. 5
15. ①③
16. -2
17.
解:![]() f(2+x)=f(2-x)
f(2+x)=f(2-x)![]() f(x)关于x=2对称,又x轴在原点右侧的第一个交点为N(6,0)
f(x)关于x=2对称,又x轴在原点右侧的第一个交点为N(6,0)
![]()
![]() =6-2=4,即T=16,
=6-2=4,即T=16,![]()
![]() =
=![]() 。
……4分
。
……4分
将N(6,0)代入f(x)=sin(![]() x+j)得:sin(
x+j)得:sin(![]() +j)=0,
+j)=0,
得:j=2k![]() +
+![]() 或j=2k
或j=2k![]() +
+![]() (kÎZ),
……8分
(kÎZ),
……8分
![]() f(0)<0,
f(0)<0,![]() j=2k
j=2k![]() +
+![]() (kÎZ),满足条件的最小正数j=
(kÎZ),满足条件的最小正数j=![]() , ……10分
, ……10分
![]() 所求解析式f(x)=sin(
所求解析式f(x)=sin(![]() x+
x+![]() )。
……12分
)。
……12分
18.
解 设![]() 依次为a,b,c,则a+b+c=6,b²=ac,
依次为a,b,c,则a+b+c=6,b²=ac,
由余弦定理得![]() , ……4分
, ……4分
故有![]() ,又
,又![]() 从而
从而![]() ……6分
……6分
(1)所以![]() ,即
,即![]() …8分
…8分
(2)所以![]()
![]() ……12分
……12分
![]() , …………14分
, …………14分
19.
解:(1)解: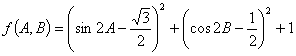 ,当
,当![]() 最小时,
最小时,
![]()
![]() 或60°,
或60°,![]() 或90°
或90°
(2)解:![]() ,
,![]()
![]() 设
设![]() ,
,![]() ,
, ![]()
![]()
20.
①已知向量![]()
若点A、B、C能构成三角形,则这三点不共线,………………2分
![]() …………5分
…………5分
故知![]() ∴实数
∴实数![]() 时,满足的条件…………8分
时,满足的条件…………8分
(若根据点A、B、C能构成三角形,必须AB+BC>CA…相应给分)
②若△ABC为直角三角形,且∠A为直角,则![]() ,
,
![]() …………10分 解得
…………10分 解得![]() …………12分
…………12分
21. 解.![]() ,或
,或![]() ,又
,又![]()
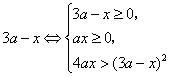 或
或![]()
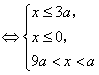 或
或![]() (以上a<0)
(以上a<0)![]() 或
或
![]() ,所以
,所以![]() ;
;
![]() ,所以
,所以![]() ,即
,即![]() ,所以
,所以![]() .
.
22.解: 可以组建命题一:△ABC中,若a、b、c成等差数列,求证:(1)0<B≤![]()
(2)![]() ;
;
命题二:△ABC中,若a、b、c成等差数列求证:(1)0<B≤![]()
(2)1<![]() ≤
≤![]()
命题三:△ABC中,若a、b、c成等差数列,求证:(1)![]()
(2)1<![]() ≤
≤![]()
命题四:△ABC中,若a、b、c成等比数列,求证:(1)0<B≤![]()
(2)1<![]() ≤
≤![]()
………………………………………………………………………………………………6分
下面给出命题一、二、三的证明:
(1)∵a、b、c成等差数列∴2b=a+c,∴b=![]()
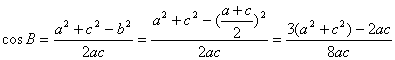 ≥
≥![]()
且B∈(0,π),∴0<B≤![]()
(2)
![]() (3)
(3)![]()
∵0<B≤![]() ∴
∴![]() ∴
∴![]() ∴
∴![]()
下面给出命题四的证明:
(4)∵a、b、c成等比数列∴b2=a+c,
![]()
且B∈(0,π),∴0<B≤![]() ………………………………………………………14分
………………………………………………………14分
评分时若构建命题的结论仅一个但给出了正确证明,可判7分;若构建命题完全正确但论证仅正确给出一个,可判10分;若组建命题出现了错误,应判0分,即坚持错不得分原则。