2006届45分钟小测试卷(三角部分)(Ⅰ)
试卷总分100分 班级 姓名 座号 成绩
一、选择题:(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的,将正确答案填入题中括号中.)
1
若![]() 为第三象限,则
为第三象限,则![]() 的值为 A.3 B.-3 C.1 D.-1
的值为 A.3 B.-3 C.1 D.-1
2 以下各式中能成立的是
( ) A.![]() B.
B.![]() 且
且![]()
C.![]() 且
且![]() D.
D.![]() 且
且![]()
3 sin7°cos37°-sin83°cos53°值 A.![]() B.
B.![]() C.
C.![]() D.-
D.-![]()
4 若函数f(x)=![]() sin
sin![]() x, x∈[0,
x, x∈[0, ![]() ], 则函数f(x)的最大值是 A
], 则函数f(x)的最大值是 A ![]() B
B ![]() C
C ![]() D
D ![]()
5
条件甲![]() ,条件乙
,条件乙![]() ,那么 A.甲是乙的充分不必要条
,那么 A.甲是乙的充分不必要条
B.甲是乙的充要条件 C.甲是乙的必要不充分条件 D.甲是乙的既不充分也不必要条件
6 ![]() 、
、![]() 为锐角a=sin(
为锐角a=sin(![]() ),b=
),b=![]() ,则a、b之间关系为
,则a、b之间关系为
A.a>b B.b>a C.a=b D.不确定
7 (1+tan25°)(1+tan20°)的值是 A -2 B 2 C 1 D -1
8 ![]() 为第二象限的角,则必有 A.
为第二象限的角,则必有 A.![]() >
>![]() B.
B.![]() <
<![]()
C.![]() >
>![]() D.
D.![]() <
<![]()
二.填空题(本大题共4小题,每小题5分,共20分。把答案填在题中横线上。)
9 若tan![]() =2,则2sin2
=2,则2sin2![]() -3sin
-3sin![]() cos
cos![]() =
。
=
。
10 若![]() -
-![]() ,
,![]() ∈(0,π),则tan
∈(0,π),则tan![]() =
。
=
。
11已知锐角![]() 终边上一点的坐标为(
终边上一点的坐标为(![]() 则
则![]() =
。
=
。
12 下列命题正确的有_________。①若-![]() <
<![]() <
<![]() <
<![]() ,则
,则![]() 范围为(-π,π);
范围为(-π,π);
②若![]() 在第一象限,则
在第一象限,则![]() 在一、三象限;③若
在一、三象限;③若![]() =
=![]() ,
,![]() ,则m∈(3,9);
,则m∈(3,9);
④![]() =
=![]() ,
,![]() =
=![]() ,则
,则![]() 在一象限。
在一象限。
三. 解答题 (本大题共4小题,共40分,解答应写出文字说明,或演算步骤)
13 (本小题满分8分)求![]() 的值。
的值。
14 (本小题满分10分) 已知sin(![]() +
+![]() )=-
)=-![]() ,cos(
,cos(![]() )=
)=![]() ,且
,且![]() <
<![]() <
<![]() <
<![]() ,
,
求sin2![]() .
.
15 (本小题满分10分)(已知![]()
求![]() 的值.
的值.
16 (本小题满分12分)设关于x的方程sinx+![]() cosx+a=0在(0, 2π)内有相异二解α、β.
cosx+a=0在(0, 2π)内有相异二解α、β.
(Ⅰ)求a的取值范围; (Ⅱ)求tan(α+β)的值.
2006届45分钟小测试卷三角(Ⅰ)参考答案
一选择题: 1.B [解析]:∵![]() 为第三象限,∴
为第三象限,∴![]()
则![]()
![]()
2.C [解析]: 若![]() 且
且![]() 则
则![]()
3.A [解析]:sin7°cos37°-sin83°cos53°= sin7°cos37°-cos7°sin37°=sin(7°- 37°)
4.D [解析]:函数f(x)=![]() sin
sin![]() x, ∵x∈[0,
x, ∵x∈[0, ![]() ],∴
],∴![]() x∈[0,
x∈[0, ![]() ],∴
],∴![]() sin
sin![]() x
x![]()
5.D [解析]:![]() , 故选D
, 故选D
6.B [解析]:∵![]() 、
、![]() 为锐角∴
为锐角∴![]()
又sin(![]() )=
)=![]() <
<![]() ∴
∴![]()
 7.B [解析]:(1+tan25°)(1+tan20°)=1+
7.B [解析]:(1+tan25°)(1+tan20°)=1+![]()
![]()
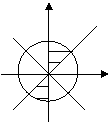
8.A [解析]:∵![]() 为第二象限的角 ∴
为第二象限的角 ∴![]() 角的终边在如图区域内
角的终边在如图区域内
∴![]() >
>![]()
二填空题: 9.![]() [解析]:2sin2
[解析]:2sin2![]() -3sin
-3sin![]() cos
cos![]() =
=![]()
10.![]() 或
或![]() [解析]:
∵
[解析]:
∵![]() -
-![]() >1,且
>1,且![]() ∈(0,π)∴
∈(0,π)∴![]() ∈(
∈(![]() ,π)
,π)
∴ (![]() -
-![]() ∴2sin
∴2sin![]() cos
cos![]() =
=![]() ∴
∴![]() +
+![]()
∴sin![]() =
=![]() cos
cos![]() =
=![]() 或sin
或sin![]() =
=![]() cos
cos![]() =
=![]() tan
tan![]() =
=![]() 或
或![]()
11.3-![]() [解析]:由三角函数定义有:tan
[解析]:由三角函数定义有:tan![]() =
=![]() = - cot 3 = tan (3 -
= - cot 3 = tan (3 - ![]() )
)
又 ∵
0<![]() <
<![]() ,0<3 -
,0<3 - ![]() <
<![]() ,∴
,∴ ![]() = 3 -
= 3 - ![]()
12.② [解析]:∵若-![]() <
<![]() <
<![]() <
<![]() ,则
,则![]() 范围为(-π,0)∴①错∵若
范围为(-π,0)∴①错∵若![]() =
=![]()
,![]() ,则m∈(3,9)
又由
,则m∈(3,9)
又由![]() 得m=0或 m=8∴m=8 故③错
得m=0或 m=8∴m=8 故③错
由![]() >0,
>0, ![]() <0且
<0且 ![]() <
< ![]() 得 2kπ+
得 2kπ+![]() <
< ![]() <2kπ+π (
<2kπ+π (![]() )
)
∴ 4kπ+![]() <
< ![]() <4kπ+2π (
<4kπ+2π (![]() ) ∴
) ∴![]() 为第四象限的角 故④错
为第四象限的角 故④错
三 解答题: 13 原式 =![]() ……2分
……2分
=![]() ……4分=
……4分=![]() =
=![]() ……6分
……6分
![]() =
=![]() ……8分
……8分
14
解: ∵![]() <
<![]() <
<![]() <
<![]() ∴
∴![]()
∵sin(![]() +
+![]() )=-
)=-![]() ,cos(
,cos(![]() )=
)=![]() ∴cos(
∴cos(![]() +
+![]() )=
)=![]() sin(
sin(![]() )=
)=![]()
∴![]() =
=![]() .
.
15
解: 由![]() =
= ![]()
=![]() 得
得![]() 又
又![]() ,所以
,所以![]() . 于是
. 于是
![]() ==
==![]() =
=![]()
16 解: (Ⅰ)∵sinx+![]() cosx=2(
cosx=2(![]() sinx+
sinx+![]() cosx)=2 sin(x+
cosx)=2 sin(x+![]() ), ∴方程化为sin(x+
), ∴方程化为sin(x+![]() )=-
)=-![]() .
.
∵方程sinx+![]() cosx+a=0在(0, 2π)内有相异二解, ∴sin(x+
cosx+a=0在(0, 2π)内有相异二解, ∴sin(x+![]() )≠sin
)≠sin![]() =
=![]() .
.
又sin(x+![]() )≠±1 (∵当等于
)≠±1 (∵当等于![]() 和±1时仅有一解), ∴-
和±1时仅有一解), ∴-![]() <1 . 且-
<1 . 且-![]() ≠
≠![]() .
.
即a<2 且a≠-![]() . ∴ a的取值范围是(-2, -
. ∴ a的取值范围是(-2, -![]() )∪(-
)∪(-![]() , 2).
, 2).
(Ⅱ) ∵α、 β是方程的相异解, ∴sinα+![]() cosα+a=0 ①. sinβ+
cosα+a=0 ①. sinβ+![]() cosβ+a=0 ②.
cosβ+a=0 ②.
①-②得(sinα- sinβ)+![]() ( cosα- cosβ)=0.
( cosα- cosβ)=0.
∴ 2sin![]() cos
cos![]() -2
-2![]() sin
sin![]() sin
sin![]() =0, 又sin
=0, 又sin![]() ≠0,
≠0,
∴tan![]() =
=![]() . ∴tan(α+β)=
. ∴tan(α+β)=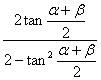 =
=![]() .
.