三角函数、平面向量专题试题集-高中三年级数学试题练习、期中期末试卷、测验题、复习资料-高中数学试卷-试卷下载

三角函数、平面向量专题试题集

1. 函数的最小正周期为　　　　　　　　　　　　　　　　　　　　　　（ A ）

　　　 A．　　　　　　　　　　 B．　　　　　　　　　　　 C．8　　　　　　　　　　　　D．4

2. 已知函数的图象的一条对称轴方程为直线x=1，若将函数的图象向右平移b个单位后得到y=sinx的图象，则满足条件的b的值一定为　　　　　　　（ C ）

　　　 A．　　　　　　　　　B．　　　　　　　　　 C．D．

3. 在△ABC，为角A、B、C所对的三条边.

　（1）求时，t的取值范围；

　（2）化简（用（1）中t表示）.

（1）∵，∴△ABC为直角三角形，

∴∠A+∠B= …………2分

又 …………4分

∵ ∴， ∴…………6分

（2）∵ ∴

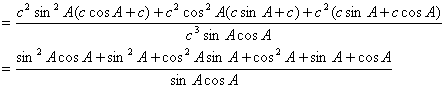
　…………9分

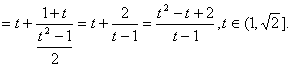　…………12分

4. 已知向量a和b的夹角为60°， a = 3， b = 4，则(2a – b)·a等于（ B ）

　（A）15　　　　　　　　（B）12　　　　　　　　（C）6　　　　　　　　（D）3

5. 已知．

　（Ⅰ）求cos的值；

　（Ⅱ）求满足sin(– x ) – sin (+ x) + 2cos=的锐角x．

解：（Ⅰ）因为，所以．　　　　（2分）

　　　　所以=，　　　　　　　（4分）

　　　　由，所以．　　　　　　（6分）

　　（Ⅱ）因为sin() – sin() + 2cos，

　　　所以，　　　　　　（8分）

　　　　所以sinx =，　　　　　　　（10分）

　　　　因为x为锐角，所以．　　　　（12分）

6. 下列函数中，最小正周期为，且图象关于直线对称的是　　　　　　　　　　　（ B ）

　　　 A．　　　　　　　　　　　　　　　 B．

　　　 C．　　　　　　　　　　　　　　　 D．

7. 若是纯虚数，则的值为　　　　　　　　　　　　　　　　　　　　（ B ）

　　　 A．　　　　　　　　　　　　　　　B．

　　　 C．　　　　　　　　　　　　　　　D．

8. 已知向量上的一点（O为坐标原点），那么的最小值是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（ B ）

　　　 A．－16　　　　　　　　　 B．－8　　　　　　　　　　 C．0　　　　　　　　　　　　D．4

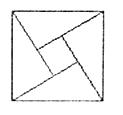9. 2002年8月，在北京召开的国际数学家大会会标如图所示，它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形，若直角三角形中较小的锐角为，大正方形的面积是1，小正方形的面积是的值等于（ D ）

　　　 A．1　　　　　　　　　　　　B．

　　　 C．　　　　　　　　　　D．－

10. 为锐角，为钝角，=.

11. 已知a=1，b=，

　（1）若a//b，求a·b；

　（2）若a，b的夹角为135°，求a+b.

解（1），

①若，同向，则　　　　　　　　　　　　　　　　　　　　　　　　 ……3分

②若，异向，则　　　　　　　　　　　　　　　　　　　　　 ……3分

　　　（2）的夹角为135°，　　　　　　　　　　　……2分

　　　　　　　　　　　　　　　　　　　　 ……2分

12.

已知函数

　　　（1）将的形式，并求其图象对称中心的横坐标；

　　（2）如果△ABC的三边a、b、c成等比数列，且边b所对的角为x，试求x的范围及此时函数f（x）的值域.

解：（1）　　　　 ……3分

　　　由

　　　即对称中心的横坐标为　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ……3分

　　　（2）由已知.

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ……3分

　　　的值域为　　　　　　　　 ……2分

　　　综上所述，　　　　　　　　　　　　　　　　　　　　　　……1分

13. 设平面上的动向量a=（s，t），b=（－1，t²－k）其中s，t为不同时为0的两个实数，实

数，满足a⊥b，

　　　（1）求函数关系式

　　　（2）若函数上是单调增函数，求证：；

　　（3）对上述，存在正项数列，其中通项公式并证明.

（1）解：　　　　　　　　　　　　　　　　　　　　　 ……3分

　　（2）证明：成立，　　　　　　　　　　　　　　　　　　　　……2分

　　　　　故；　　　　　　　　　　　　　　　　　　　　　　　　　　　　……1分

　（3）

　　　　　故

　　　　因为　　……4分

　　　　　事实上，

　　　　　　　　　　　　　　　　　　　　　　　　　　　　……4分

　　　方法1：

　　　方法2：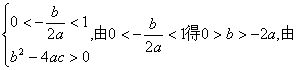

14. 如果函数的最小正周期是T，且当时取得最大值，那么（ A ）

A．　 B．　 C．　 D．

15. 在中，已知，那么一定是（ B ）

A．直角三角形　B．等腰三角形 C．等腰直角三角形　D．正三角形

16. 已知，那么的值为，的值为。

17. 若，且（）⊥ ，则与的夹角是　　（ B ）

（A）　　　　（B）　　　　（C）　　　　（D）

18. 把y = sinx的图象向左平移个单位，得到函数y = sin的图象；再把所得图象上的所有点的横坐标伸长到原来的2倍，而纵坐标保持不变，得到函数的图象。

19. 已知直线：x – 2y + 3 = 0 ，那么直线的方向向量为（2，1）或等(注：只需写出一个正确答案即可)；过点（1，1），并且的方向向量₂与₁满足₁·= 0，则的方程为2x + y – 3 = 0。

20. 已知：tan= 2，求：

（Ⅰ）tan的值；

　　（Ⅱ）sin2的值．

解：（Ⅰ）== 2，∴tan．　　　（5分）

　　　　　　　（Ⅱ）解法一：

　　　　　　　　　　　 sin2+sin²+ cos²= sin²+ sin²+ cos²– sin²

　　　　　　　　　　　 = 2sincos+ cos²　　　　　　　　　　　　（8分）

　　　　　　　　　　　 = 　　　　　（11分）

　　　　　　　　　　　 =．　　　　（13分）

　　　　　　（Ⅱ）解法二：

　　　　　　　　　　　 sin2+ sin²+ cos2= sin2+ sin²+ cos²– sin²

　　　　　　　　　　　 = 2sincos+ cos² （1）　　　　　　　　　　　　　　　　　（8分）

　　　　　　　　　　　 ∵tan=，∴为第一象限或第三象限角．

　　　　　　　　　　　当为第一象限角时，sin=，cos=，代入（1）得

　　　　　　　　　　　 2sincos+ cos²=；　　　　　（10分）

　　　　　　　　　　　当为第三象限角时，sin=，cos=，代入（1）得

　　　　　　　 2sincos+ cos²=．　　（12分）

　　　　　　　　　　　综上所述：sin2+ sin²+ cos2=．　　　（13分）

21. 已知常数a > 0，向量，，经过定点A (0，– a )以+为方向向量的直线与经过定点B (0，a)以+ 2为方向向量的直线相交于点P，其中∈R．

　（Ⅰ）求点P的轨迹C的方程；

　（Ⅱ）若，过E (0，1)的直线l交曲线C于M、N两点，求的取值范围．

解：（Ⅰ）设P点的坐标为(x，y)，则，，

　　　　　　　　　　　又，故，．

　　　　　　　　　　　由题知向量与向量平行，故(y + a) = ax．

　　　　　　　　　　　又向量与向量平行，故y – a = 2．

　　　　　　　　　　　两方程联立消去参数，得点P (x，y)的轨迹方程是

　　　　　　　　　　　 (y + a)(y – a) = 2a²x²，即y² – a² = 2a²x²．　　　　（6分）

　　　　　（Ⅱ）∵，故点P的轨迹方程为2y² – 2x² = 1，

　　　　　　　　　　　此时点E (0，1)为双曲线的焦点．

　　　　　　　　　　　 ①若直线l的斜率不存在，其方程为x = 0，l与双曲线交于、

，此时．　（8分）

　　　　　　　 ②若直线l的斜率存在，设其方程为y = kx + 1，代入2y² – 2x² = 1化简得

　　　　　　　　 2(k² – 1) x² + 4kx + 1 = 0．

∴直线l与双曲线交于两点，

∴△= (4k)² – 8 (k² – 1) > 0且k² – 1≠0．解得k≠±1．

设两交点为M (x₁，y₁)、N (x₂，y₂)，

则x₁ + x₂ =，x₁x₂ =．　　（10分）

此时

= x₁x₂ + k²x₁x₂ = (k² + 1) x₁x₂ =．

当– 1 < k < 1时，k² – 1 < 0，故≤；

当k > 1或k < – 1时，k² – 1 > 0，故．

综上所述，的取值范围是∪．　（13分）

22.

数学三角考点综合讲解与训练(2)

23.

24.

25.

数学三角考点综合讲解与训练(3)

26.

27.

28.

数学三角考点综合讲解与训练(4)

29.

30.

数学三角考点综合讲解与训练(5)

31.

32. 已知向量＝(8， x)，＝(x，1)，其中x＞0，若(－2)∥(2＋)，则x的值为
A.4　　　　　　　　　　　　　　　　　B.8　　　　　　　　　　　　　　　C.0　　　　　　　　　　　　　　　D.2
解：－2＝(8－2x，x－2)，2＋＝(16＋x，x＋1)
由(－2)∥(2＋)，得(8－2x，x－2)＝λ(16＋x，x＋1)
即　Þ　x＝4.选A

33. 同时具有以下性质：“①最小正周期实π；②图象关于直线x＝对称；③在[－]上是增函数”的一个函数是
A.y＝sin()　　　　　　　　 B.y＝cos(2x＋)　　　　　 C.y＝sin(2x－)　　　　　　D.y＝cos(2x－)
解：由性质①排除A，由性质②排除D，由性质③排除B，选C.

34. 在△ABC中，已知sin2Asin2B＝，tanAtanB＝3，求角C.
解：∵sin2Asin2B＝，∴sinAsinBcosAcosB＝　　 ……①　　　……3'
　由A、B∈(0，π)，知sinAsinB＞0，∴cosAcosB＞0
　又tanAtanB＝3，即＝3　　　　　　　　 ……②　　　……6'
由①②得：
∴cosC＝－cos(A＋B)＝－cosAcosB＋sinAsinB＝
而C∈(0，π)，∴C＝.

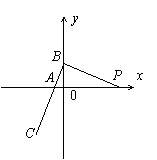35. 如图，已知点P(3，0)，点A、B分别在x轴负半轴和y轴上，且＝0，，当点B在y轴上移动时，记点C的轨迹为E.
(1)求曲线E的方程；
(2)已知向量＝(1，0)，＝(0，1)，过点Q(1，0)且以向量＋k(k∈R)为方向向量的直线l交曲线E于不同的两点M、N，若D(－1，0)，且＞0，求k的取值范围.
解：(1)设A(a，0)(a＜0)，B(0，b)，C(x，y)
则＝(x－a，y)，＝(a，－b)，＝(3，－b)，
∵＝0，，
∴　　　　　　　　　　　　 ……3'
消去a、b得：y²＝－4x
∵a＜0，∴x＝3a＜0
故曲线E的方程为y²＝－4x(x＜0)　　　　　　　　 ……5'
(2)设R(x，y)为直线l上一点，由条件知)
即(x－1，y)＝λ(1，k)
∴，消去λ得l的方程为：y＝k(x－1)　 ……7'
由Þk²x²－2(k²－2)x＋k²＝0　 ……(*)
∵直线l交曲线E与不同的两点M、N
∴△＞0　Þ　－1＜k＜1　　　　　　　　 ……①　……9'
设M(x₁，y₁)，N(x₂，y₂)，则＝(x₁＋1，y₁)，＝(x₂＋1，y₂)
∵M、N在直线y＝k(x－1)上，
∴y₁＝k(x₁－1)，y₂＝k(x₂－1)
又由(*)，有x₁＋x₂＝，x₁x₂＝2
∴＝(x₁＋1)(x₂＋1)＋y₁y₂
　　　　＝(x₁＋1)(x₂＋1)＋k²(x₁－1)(x₂－1)
　　　　＝(k²＋1)x₁x₂＋(1－k²)(x₁＋x₂)＋k²＋1
　　　　＝
由条件知：＞0　Þk²＞　　　　　 ……②　……12'
由①②知：－1＜k＜－或＜k＜1.　　　　　 ……13'