三山高级中学 高三文科第一次月考数学试卷
高三文科第一次月考数学试卷
一.选择题(每题5分,共50分)
1.已知全集![]() ,集合
,集合![]() ,集合
,集合![]() ,则集合
,则集合![]() 等于┄┄( )
等于┄┄( )
A.{3,4,5} B.{3,5}
C.{4,5}
D.![]()
2.已知数列![]() 是等差数列,且
是等差数列,且![]() 则数列
则数列![]() 的公差等于┄┄┄┄┄( )
的公差等于┄┄┄┄┄( )
A.1 B.4 C.5 D.6
3.已知函数![]() ,那么
,那么![]() 的值为┄┄┄┄┄┄┄┄┄┄┄┄┄( )
的值为┄┄┄┄┄┄┄┄┄┄┄┄┄( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.条件![]()
![]() ,条件
,条件![]()
![]() ,则
,则![]() 是
是![]() 的┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄( )
的┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄( )
A.充分但不必要条件 B.必要但不充分条件
C.充分且必要条件 D.既不充分也不必要条件
5.若定义在区间![]() 内的函数
内的函数![]() 满足
满足![]() ,则实数
,则实数![]() 的取值范围为( )
的取值范围为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.在各项均为正数的等比数列![]() 中,若
中,若![]() ,则
,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.将函数![]() 图象沿
图象沿![]() 轴向左平移一个单位,再沿
轴向左平移一个单位,再沿![]() 轴翻折
轴翻折![]() ,得到
,得到![]() 的图象,则( )
的图象,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.函数![]() 的图象大致为┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄( )
的图象大致为┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄( )
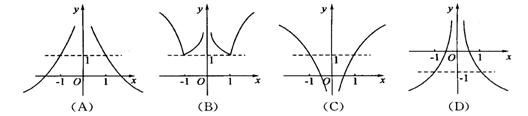
9.已知![]() ,若
,若![]() ,则
,则![]() 值的符号为┄┄┄┄┄┄┄┄( )
值的符号为┄┄┄┄┄┄┄┄( )
A.正号 B.零 C.负号 D.不能确定
10.小王从2000年起,每年1月1日到工商银行存入![]() 元一年定期储蓄,若年利率为
元一年定期储蓄,若年利率为![]() 且保持不变,
且保持不变,
并约定每年到期存款均自动转为新的一年定期,到2007年1月1日将所有存款和利息全部取回,
则可取回的钱的总数(元)为┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二.填空题(每格4分,共16分)
|
|
|
|
|
|
|
|
11.若指数函数的部分对应值如右表:
则不等式![]() 的解集为
.
的解集为
.
12.函数![]() 的定义域为
.
的定义域为
.
13.已知函数![]() ,
,![]() ,则
,则![]() .
.
14.不等式![]() 对一切
对一切![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围为
.
的取值范围为
.
三.解答题(每小题14分,共84分)
15.已知![]() 为等比数列,
为等比数列,![]() ,
,![]() .
.
⑴ 求数列![]() 的公比
的公比![]() ;
;
⑵ 求数列![]() 的前项和
的前项和![]() .
.
16.已知集合![]() ,
,![]() .
.
若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
17.设![]() ,已知
,已知![]() 是奇函数.
是奇函数.
⑴ 求![]() 的值;
的值;
⑵ 求![]() 的单调区间和极值.
的单调区间和极值.
18.已知数列![]() 的前
的前![]() 项和为
项和为![]() ,并且满足
,并且满足![]() ,
,![]() .
.
⑴ 求数列![]() 的通项公式;
的通项公式;
⑵ 令![]() ,当
,当![]() 时,求证:
时,求证:![]() .
.
19.设![]() 是定义在
是定义在![]() 上的函数,对任意
上的函数,对任意![]() ,恒有
,恒有![]() ,
,
当![]() 时,有
时,有![]() .
.
⑴ 求证:![]() ,且当
,且当![]() 时,
时,![]() ;
;
⑵ 证明:![]() 在
在![]() 上单调递减;
上单调递减;
20.已知二次函数![]() ,满足
,满足![]() .
.
⑴ 求b的值;
⑵ 当![]() 时,求函数
时,求函数![]() 的反函数
的反函数![]() ;
;
⑶ 对于⑵中的![]() ,如果
,如果![]() 在
在![]() 上恒成立,
上恒成立,
求实数m的取值范围.

 三山高级中学
三山高级中学 高三文科第一次月考数学答卷
高三文科第一次月考数学答卷
一.选择题(每题5分,共50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二.填空题(每格4分,共16分)
11. 12.
13. 14.
三.解答题(每小题14分,共84分)
| |
 16.
16.
 17.
17.
 18.
18.
 19.
19.

 20.
20.
 三山高级中学
三山高级中学 高三文科第一次月考数学卷参考答案
高三文科第一次月考数学卷参考答案
一.选择题(每题5分,共50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | B | B | A | A | B | C | A | A | D |
二.填空题(每格4分,共16分)
11.![]() 12.
12.![]() 13.
13.![]() 14.
14.![]()
三.解答题(每小题14分,共84分)
15.解:⑴ 由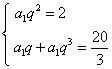 4分 得
4分 得 ![]() 6分
6分
⑵ 当![]() 时,有
时,有![]() ,
,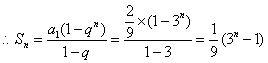 10分
10分
当![]() 时,有
时,有![]() ,
,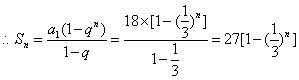 14分
14分
16.解:由于![]() ,
,![]() 2分
2分
当![]() 时,有
时,有![]() , 5分
, 5分 ![]() 7分
7分
当![]() 时,由韦达定理知
时,由韦达定理知![]() , 10分
, 10分![]() 12分
12分
![]() 实数
实数![]() 的取值范围为:
的取值范围为:![]() 或
或![]() 14分
14分
17.解:⑴![]() 1分
1分
![]() 2分
2分
由于![]() 是奇函数,
是奇函数,![]() ,即
,即![]() 4分
4分
![]() 6分
6分
⑵ 由⑴知:![]() ,
,![]() 8分
8分
令![]() ,得
,得![]() 或
或![]() ;令
;令![]() ,得
,得![]() ,10分
,10分
![]()
![]() 的增区间为
的增区间为![]() ;
;![]() 的增区间为
的增区间为![]() ;12分
;12分
当![]() 时,有
时,有![]() ;当
;当![]() 时,有
时,有![]() . 14分
. 14分
18.解:⑴ 当![]() 时,由
时,由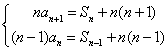 两式相减得: 2分
两式相减得: 2分
![]() ,即
,即![]() ,又
,又 ![]() 4分
4分
![]()
![]() 是以
是以![]() 为首项,以
为首项,以![]() 为公差的等差数列. 6分
为公差的等差数列. 6分
![]()
![]() 7分
7分
⑵ 由⑴知:![]() ,
, ![]() 9分
9分
由于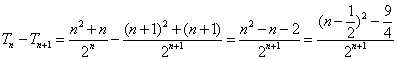 得 11分
得 11分
![]() ,
,![]() ,
,![]()
![]() 14分
14分
19.解:⑴ 令![]() 得
得![]() 2分
2分
当![]() 时,有
时,有![]() ,
,![]()
![]() 4分
4分
当![]() 时,有
时,有![]() ,
,![]() ,又
,又![]()
![]() 7分
7分
⑵ 设![]() 且
且![]()
![]() 9分
9分
又![]() 12分
12分
![]()
![]()
![]() 在
在![]() 上单调递减.
14分
上单调递减.
14分
20.解:⑴![]()
解得![]() .(或利用对称性求解)
3分
.(或利用对称性求解)
3分
⑵ 由⑴,![]()
![]()
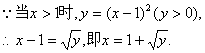
![]() .
7分
.
7分
⑶![]()
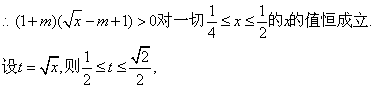
![]() 9分
9分
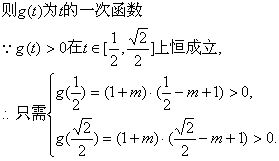
解得![]() 13分
13分
![]() 的取值范围是:
的取值范围是:![]() .
14分
.
14分