山东省实验中学2006年2月高三统一考试数学试卷(文史类)
本试卷分第I卷(选择题)和第II卷(非选择题)两部分。
第I卷(选择题 共60分)
一、选择题:本大题共12小题。每小题5分;共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 已知![]() ,若
,若![]() ,则实数a的取值范围是( )
,则实数a的取值范围是( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
2. 若a,b均为非零向量,则“![]() ”是“
”是“![]() ”的( )
”的( )
A. 充要条件 B. 必要不充分条件
C. 充分不必要条件 D. 即不充分也不必要条件
3. 有8个大小相同的球,上面分别标有1,2,3,4,5,6,7,8,现任取两个球,则两个球的序号不相邻的概率是( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
4. 设![]() ,则有( )
,则有( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
5. 把函数![]() 的图象按向量a平移,得到函数
的图象按向量a平移,得到函数![]() 的图象,则a等于( )
的图象,则a等于( )
A. (-3,-4) B.(3,4) C. (-3,4) D. (3,-4)
6. 已知函数![]() 的反函数是
的反函数是![]() ,若
,若![]() ,则ab的值为( )
,则ab的值为( )
A. 4 B. 8 C. 12 D. 16
7. 下列命题中真命题的个数有:
(1)若![]() ,那么
,那么![]() ;
;
(2)已知![]() 都是正数,并且
都是正数,并且![]() ,则
,则![]() ;
;
(3)若![]() ,则
,则![]() ;
;
(4)![]() 的最大值是
的最大值是![]() 。
。
A. 3个 B. 2个 C. 1个 D. 0个
8. P、A、B、C是球O面上的四个点,PA、PB、PC两两垂直,且![]() ,则球的体积为( )
,则球的体积为( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
9. 已知二项式![]() 的展开式中含
的展开式中含![]() 的项是第4项,则n的值为( )
的项是第4项,则n的值为( )
A. 7 B. 8 C. 9 D. 10
10. 已知双曲线![]() 的一条渐近线与直线
的一条渐近线与直线![]() 垂直,则该双曲线的准线方程是( )
垂直,则该双曲线的准线方程是( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
11. 在△ABC中,B(-2,0),C(2,0),A(x,y)。若△ABC满足的条件分别为①周长为10;②∠A=90°;③![]() ;则A的轨迹方程分别是a:
;则A的轨迹方程分别是a:![]() ;b:
;b:![]() ;c:
;c:![]() 则正确的配对关系是( )
则正确的配对关系是( )
A. ①a②b③c B. ①b②a③c C. ①c②a③b D. ①b②c③a
12. 设![]() ,常数a>0,定义运算“*”:
,常数a>0,定义运算“*”:![]() ,若
,若![]() ,则动点
,则动点![]() 的轨迹是( )
的轨迹是( )
A. 圆 B. 椭圆的一部分
C. 双曲线的一部分 D. 抛物线的一部分
第II卷(非选择题 共90分)
二、填空题:本大题共4小题。每小题4分;共16分。把答案填在题中横线上。
13. 若工厂生产A、B、C三种不同型号的产品,产品数量之比依次为3:4:7,现用分层抽样法抽出一个容量为n的样本,样本中B型号产品有28件,那么样本的容量n=__________。
14. 抛物线![]() 与直线
与直线![]() 交于两点A、B,设抛物线的焦点为F,则
交于两点A、B,设抛物线的焦点为F,则![]() 等于___________。
等于___________。
15. 已知,直线a、b、c和平面α、β,给出下列命题:
①若a、b与α成等角,则a//b;
②若α//β,c⊥α,则c⊥β;
③若a⊥b,a⊥α,则b//α;
④若α⊥β,a//α,则a⊥β
其中错误命题的序号是________________。
16. 用类比推理的方法填表
| 等差数列 | 等比数列 |
|
|
|
|
|
|
|
|
三、解答题:本大题共6小题。共74分。解答应写出文字说明、证明过程或演算步骤。
17. (本小题满分12分)
已知函数![]() 在
在![]() 和
和![]() 处取得极值,
处取得极值,
(1)确定函数![]() 的解析式;
的解析式;
(2)求函数![]() 的单调区间。
的单调区间。
18. (本小题满分12分)
已知函数![]() 的图象在y轴右侧的第一个最高点(函数取最大值的点)为P(
的图象在y轴右侧的第一个最高点(函数取最大值的点)为P(![]() ,2),在原点右侧与x轴的第一个交点为H(
,2),在原点右侧与x轴的第一个交点为H(![]() ,0)。
,0)。
(1)求函数![]() 的解析式;
的解析式;
(2)求函数![]() 在区间[
在区间[![]() ]上的对称轴方程。
]上的对称轴方程。
19. (本小题满分12分)
某人抛掷一枚质量分布均匀的骰子,出现各数的概率都是![]() ,构造数列
,构造数列![]() ,使
,使 ,记
,记![]()
(1)求![]() 时的概率;
时的概率;
(2)求![]() 时的概率;
时的概率;
(3)若前两次均为奇数,求![]() 时的概率。
时的概率。
20. (本小题满分12分)
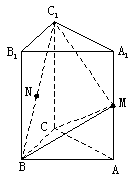
如图,在直三棱柱ABC![]() 中,
中,![]() ,∠ACB=90°,M是
,∠ACB=90°,M是![]() 的中点,N是
的中点,N是![]() 的中点。
的中点。
(1)求证:MN//平面![]() ;
;
(2)求点![]() 到平面MBC的距离;
到平面MBC的距离;
(3)求二面角![]() 的大小。
的大小。
21. (本小题满分12分)
已知一列非零向量![]() 满足:
满足:![]() ,
,![]()
![]()
(1)证明:![]() 是等比数列;
是等比数列;
(2)设![]() ,求
,求![]() 。
。
22. (本小题满分14分)
已知![]() 是椭圆
是椭圆![]() 的左、右焦点,A是椭圆上位于第一象限内的一点,点B也在椭圆上,且满足
的左、右焦点,A是椭圆上位于第一象限内的一点,点B也在椭圆上,且满足![]() (0是坐标原点),
(0是坐标原点),![]() 。若椭圆的离心率等于
。若椭圆的离心率等于![]() 。
。
(1)求直线AB的方程。
(2)若三角形![]() 的面积等于
的面积等于![]() ,求椭圆的方程;
,求椭圆的方程;
(3)证明:在(2)的条件下,椭圆上不存在点M,使得三角形MAB的面积等于![]() 。
。
高三数学(文史类)模拟试题参考答案及评分标准
一、1. C 2. A 3. C 4. C 5. A
6. D 7. B 8. D 9. C 10. D
11. B 12. D
二、13. 98 14. 7
15. ①③④ 16.
![]()
三、17. 解:(1)![]()
![]() 2分
2分
又![]() 在
在![]() 和
和![]() 处取得极值
处取得极值
 4分
4分
![]()
![]() 6分
6分
(2)由![]()
若![]() 则
则![]() 或
或![]() 8分
8分
若![]() 则
则![]() 9分
9分
∴函数![]() 的单调减区间为[-2,
的单调减区间为[-2,![]() ] 10分
] 10分
函数![]() 的单调增区间为
的单调增区间为![]() 和
和![]() 12分
12分
18. 解:(1)易知![]() 2分
2分
![]() 4分
4分
将点P(![]() )代入
)代入![]() ,
,
即![]() ,易得
,易得![]() 7分
7分
故所求解析式为![]() 8分
8分
(2)由![]() 得
得![]() 9分
9分
令![]()
![]()
![]() 11分
11分
故所求对称轴为![]() 12分
12分
19. 解:(1)即求第4次掷出偶数的概率![]() 4分
4分
(2)若![]() 即在4次抛掷中,有一次奇数,3次偶数 6分
即在4次抛掷中,有一次奇数,3次偶数 6分
∴概率为:![]() 8分
8分
(3)若前2次为奇数,且![]() ,则应满足:在后5次抛掷中有3次掷偶数,2次掷奇数 10分
,则应满足:在后5次抛掷中有3次掷偶数,2次掷奇数 10分
∴概率![]() 12分
12分
20. 解法一:
(1)证明:取![]() 的中点D,连结ND、A1D、NM
的中点D,连结ND、A1D、NM
可知DN//BB1//AA1 1分
∵N是BC1的中点
![]() 2分
2分
∴四边形A1MND为平行四边形
∴MN//A1D 3分
又MN![]() 平面
平面![]() ,A1D
,A1D![]() 平面
平面![]()
∴MN//平面![]() 4分
4分
(2)解:∵三棱柱![]() 是直三棱柱
是直三棱柱
![]() 又
又![]() 5分
5分
∴BC⊥平面A1MC1 6分
在平面![]() 中,作
中,作![]() 于H,又
于H,又![]() 面
面![]()
![]()
![]() 为C1到平面MBC的距离 7分
为C1到平面MBC的距离 7分
由题意![]()
∴△CMC1为正三角形
![]()
![]() 即C1到平面BMC的距离为
即C1到平面BMC的距离为![]() 8分
8分
(3)在平面![]() 上作
上作![]() ,交
,交![]() 于点E,连结BE
于点E,连结BE
则CE为BE在平面![]() 上的射影
上的射影
∴BE⊥C1M 9分
作![]() 交
交![]() 于F,则
于F,则![]() 为二面角
为二面角![]() 的平面角 10分
的平面角 10分
在等边△CMC1中,![]()
![]() 11分
11分
![]()
![]()
∴二面角![]() 的大小为
的大小为![]() 12分
12分
解法二:
(1)证明:如图,以点C为坐标原点,以CB所在直线为x轴,CA所在直线为y轴,![]() 所在直线为z轴,建立空间直角坐标系,取
所在直线为z轴,建立空间直角坐标系,取![]() 中点D 1分
中点D 1分
由已知,得![]() ,
,![]() ,
,![]() ,
,![]() 2分
2分
![]() 3分
3分
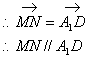
又![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴MN//平面![]() 4分
4分
(2)B(![]() ,0,0),C(0,0,0),
,0,0),C(0,0,0),![]() ,
,![]() 5分
5分
设垂直于平面BCM的向量![]()
则![]() 6分
6分
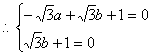
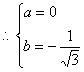
![]() 7分
7分
![]() 到平面BMC的距离
到平面BMC的距离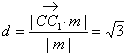 8分
8分
(3)三棱柱![]() 为直三棱柱
为直三棱柱
![]()
又∠ACB=90°
![]() 平面
平面![]() 9分
9分
设垂直于平面![]() 的向量
的向量![]() ,
,![]()
![]()
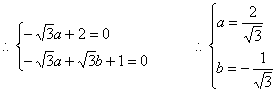 10分
10分
![]()
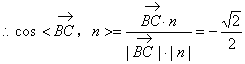 11分
11分
![]()
∴二面角的度数为![]() 12分
12分
21. 解:(1)![]() 1分
1分
![]() 3分
3分
![]() ,且
,且![]() 4分
4分
![]() 是公比为
是公比为![]() 的等比数列 5分
的等比数列 5分
(2)![]()
![]() 6分
6分
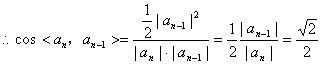 8分
8分
![]() 9分
9分
![]() 10分
10分
即![]()
![]() 12分
12分
22. (1)由![]() 知,直线AB经过原点,又由
知,直线AB经过原点,又由![]() 知
知![]() ,因为椭圆的离心率等于
,因为椭圆的离心率等于![]() ,所以
,所以![]() ,故椭圆方程为
,故椭圆方程为![]() 1分
1分
设A(x,y),由![]() ,知x=c 2分
,知x=c 2分
∴A(c,y),代入椭圆方程得![]()
![]() ,故直线AB的斜率
,故直线AB的斜率![]() 3分
3分
因此直线AB的方程为![]() 4分
4分
(2)连结![]() ,由椭圆的对称性可知
,由椭圆的对称性可知
![]() ,所以
,所以![]() 6分
6分
又由![]() 解得
解得![]() 7分
7分
故椭圆方程为![]() 8分
8分
(3)由(2)可以求得![]() 9分
9分
假设在椭圆上存在点M使得三角形MAB的面积等于![]()
设点M到直线AB的距离为d,则应有![]() 10分
10分
∴d=4 11分
设点P(![]() )为椭圆上任意一点
)为椭圆上任意一点
则P到直线![]() 的距离为
的距离为

故椭圆上不存在点M使得三角形MAB的面积等于![]() 14分
14分