山西省临汾一中高三理科第一次月考数学试题

山西省临汾一中高三理科第一次月考数学试题（理）

（2006.8）

一.选择题（12×5＝60分）

1．设随机变量ξ的分布列为P(ξ=i )=a, i=1,2,3，则a的值为（ D ）

A.　1　　　  B.　　　　　C.　　　　　 D.　　

2．要从已编号（1-50）的50枚最新研制的某型号导弹中随机抽取5枚来进行发射试验，用每部分选取的号码间隔一样的系统抽样方法,确定所选取的5枚导弹的编号可能是（ B ）

A.　5、10、15、20、25　　　　　　　　 B.　3、13、23、33、43

C.　1、2、3、4、5　　　　　　　　　　 D.　2、4、8、16、22

3．若ξ~ B(n， p)，且Eξ＝6，Dξ＝3，则P(ξ=1)的值为（ C ）

A.　　　B.　 　　 C.　 　　 D.

4.等于（ B ）

A.  1　　　　  B.　　　　　 C.　 0　　　　D.　

5. 已知，若，则的值是　（ D　 ）

A．　　　　　 B．　 　　 C．　　 　　D．

6.曲线上一点P处的切线平行于轴,则点P的坐标是（ D　）

　A．（-1，2）　　　B．（1，-2）　　 C．（1，2）　　 D．（-1，2）或（1，-2）

7.设随机变量ξ~ N(μ，σ² )，且 P(ξ)= P(ξ)，则c =（　C　 ）

A.　 σ²　　　　  B.　　σ　　　 C.　　 μ　　　 D. 　 –μ

8.新生儿体重的频率分布直方图如下，则新生儿体重在（2700，3000）的频率为

A.0.001　　　　　 B.0.1　　　  C.0.2　　　　　　 D.0.3

　　　

9.设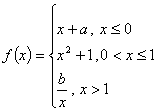，在定义域内连续，则的值分别是（A

A. 　　B. 　C. 　D.

10．某社区有500户家庭，其中高收入家庭125户，中等收入家庭280户，低收入家庭95户，为了调查社会购买力的某项指标，要从中抽取1个容量为100户的样本，记作①；某学校高三年级有12名足球运动员，要从中选出3人调查学习负担情况，记作②。那么完成上述两项调查应采用的抽样方法是（ B ）

A. ①用随机抽样法，②用系统抽样法　 B. ①用分层抽样法，②用随机抽样法

C. ①用系统抽样法，②用分层抽样法　 D. ①用分层抽样法，②用系统抽样法

11. 某个与正整数有关的命题，若当时该命题成立，则可推出当时该命题也成立，现已知当时该命题不成立，那么可推得（D ）

A. 当n=6时，该命题成立　　　 B. 当n=6时，该命题不成立

C. 当n=4时，该命题成立　　　 D. 当n=4时，该命题不成立

12. 设，则等于

（ B ）

 A．　　　　  B．－　　　 C．　　　　 D．－

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案

二.填空题（4×4＝16分）

13. 函数的不连续点是　　　　　　 .

14. 某公司有5万元资金用于投资开发项目，如果成功，一年后可获利10%，一旦失败，一年后将丧失全部资金的50%，下表是过去200例类似项目开发的实施结果：

投资成功	投资失败
192次	8次

则该公司一年后估计可获收益的期望是__________（元）.

15．某县三个镇共有高中生2000名，且这三个镇高中生人数之比2：3：5，若学生甲被抽到的概率为，则这三个镇被抽到的高中生人数分别为________，________，________.

16.随机变量ξ的概率分布规律为其中是常数，则 的值为　　　　　　 　.　　　　　

三.解答题（共74分）

17. （12分）求下列极限：

（1）　　　　　　　　　　　　　　　　　　 ；

（2）　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 .

18. （12分）求下列函数的导数：

（1）　；　　（2）　　　　　　　  .

19. （14分）从5名女生和2名男生中任选3人参加英语演讲比赛，设随机变量表示所选3人中男生的人数.

　（1）求的分布列；　 （2）求的数学期望；

（3）求“所选3人中男生人数”的概率.

20.（12分）张三开车回家途中有6个交通岗，他在每个路口遇到红灯的事件是相互独立的，并且概率都是

（1）设为他在途中遇到的红灯次数，求的期望和方差；

（2）设表示他在首次停车前经过的路口数，求的分布列。

21. （12分）已知数列(8×1)/(1²×3²)，(8×2)/(3²×5²)，…，(8×n)/[(2n－1)²×(2n＋1)²]，…，S_n为其前n项和。计算得S₁＝8/9，S₂＝24/25，S₃＝48/49，S₄＝80/81，观察上述结果,推测出计算S_n的公式，并用数学归纳法加以证明。

22．（12分）

在某校举行的数学竞赛中，全体参赛学生的竞赛成绩近似服从正态分布。已知成绩在90分以上（含90分）的学生有12名。

（Ⅰ）、试问此次参赛学生总数约为多少人？

（Ⅱ）、若该校计划奖励竞赛成绩排在前50名的学生，试问设奖的分数线约为多少分？

可共查阅的（部分）标准正态分布表

	0	1	2	3	4	5	6	7	8	9
1.2 1.3 1.4 1.9 2.0 2.1	0.8849 0.9032 0.9192 0.9713 0.9772 0.9821	0.8869 0.9049 0.9207 0.9719 0.9778 0.9826	0.888 0.9066 0.9222 0.9726 0.9783 0.9830	0.8907 0.9082 0.9236 0.9732 0.9788 0.9834	0.8925 0.9099 0.9251 0.9738 0.9793 0.9838	0.8944 0.9115 0.9265 0.9744 0.9798 0.9842	0.8962 0.9131 0.9278 0.9750 0.9803 0.9846	0.8980 0.9147 0.9292 0.9756 0.9808 0.9850	0.8997 0.9162 0.9306 0.9762 0.9812 0.9854	0.9015 0.9177 0.9319 0.9767 0.9817 0.9857

山西省临汾一中高三理科第一次月考数学试题（理）答案

一.选择题（12×5＝60分）

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案	D	B	C	B	D	D	C	D	A	B	D	B

二.填空题（4×4＝16分）

13. x=1,x=2 　　14. 3800　　　15. 40、60、100　　 16.

三.解答题（74分）

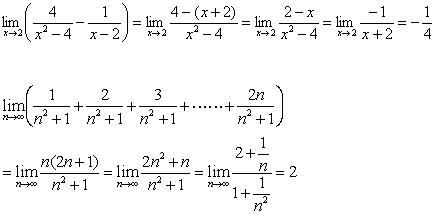17.解：（1）

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  6分

（2）

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 12分

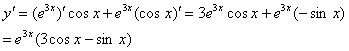18.解：（1）

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　6分

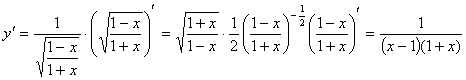（2）

另解：　 12分

　　　　　　　　　　　　　　　　　　　　　　　　　　　 

19.（1）解：可能取的值为0，1，2，

0 1 2 P

所以的分布列为：　　　　　　　　　　　　　　　　　　　  （6分）

 （2）解：由（1）的数学期望为　 （10分）

 （3）由（1），“所选3人中男生人数”的概率为

　　　　　　　　　　 （14分）

20.解：（1）张三在6个路口遇到红灯是相互独立的，在每个路口遇到红灯的概率都是，则P（=K）=(k=0,1,2,3,4,5,6) ,则服从B（6，），则E=6=2（次），D=6=。　　　　　　　　　　　　　　　　　　 （6分）

（2）的可能的取值为0、1、2、3、4、5、6

　 P（=0）=　　　　　　　　　　　　　

 P（=1）=（）=

　 P（=2）=（）²=

 P（=3）=（）³=

　 P（=4）=（）⁴=

　 P（=5）=（）⁵=

　 P（=6）=（）⁶=

则的分布列如下：表格略　　　　　　　　　  （12分）

21.本小题考查观察、分析、归纳的能力和数学归纳法.
解：S_n＝[(2n＋1)²－1]/(2n＋1)²　(n∈N)
证明如下：
(Ⅰ)当n＝1时，S_１＝[3²－1]/3²＝8/9，等式成立。
(Ⅱ)设当n=k时等式成立,即
　　
　　　　　
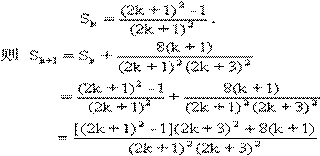
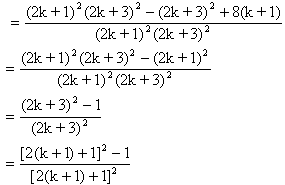
由此可知,当n=k+1时等式也成立.
根据(Ⅰ)、(Ⅱ)可知,等式对任何n∈N都成立.　　　　　　　  12分

22.解：（Ⅰ）设参赛学生的分数为，因为～N(70，100)，由条件知，

P(≥90)＝1－P（<90）＝1－F(90)＝1－＝1－(2)＝1－0.9772＝0.0228.

这说明成绩在90分以上（含90分）的学生人数约占全体参赛人数的2.28％，因此，

参赛总人数约为≈526（人）。　　　　　　　　　　　  6分

（Ⅱ）假定设奖的分数线为x分，则

P(≥x)＝1－P（<x）＝1－F(x)＝1－＝＝0.0951，

即＝0.9049，查表得≈1.31，解得x＝83.1.

故设奖得分数线约为83.1分。　　　　  　　　　　　　　　　 12分