|
2006届高三十月份月考试题
数学（文科）
一、选择题：（本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）
1．设集合A={
= （ ）
A．
B．
C．
D．
2．函数f(x)是定义在R上的偶函数，在
上是减函数，且f(2)=0，则使得f(x)<0成立的
x的取值范围是 （ ）
A．（－∞，2） B．（2，+∞）
C．（－∞，－2）∪（2，+∞） D．（－2，2）
3．为了得到函数y=2x－3－1的图象，只需把函数y=2x图象上的所有点 （ ）
A．向右平移3个单位长度，再向下平移1个单位长度
B．向左平移3个单位长度，再向下平移1个单位长度
C．向右平移3个单位长度，再向上平移1个单位长度
D．向左平移3个单位长度，再向上平移1个单位长度
4．函数
反函数是 （ ）
A．y=1+
(－1≤x≤1) B．y=1+(0≤x≤1)
C．y=1－(－1≤x≤1) D．y=1－(0≤x≤1)
5．设I为全集，S1、S2、S3是I的三个非空子集，且S1∪S2∪S3=I，则下面论断正确的是（ ）
A．C1S1∩(S2∪S3)=φ B．S1
（C1S2∩C1S3）
C．C1S1∩C1S2∩C1S3=φ D．S1（C1S2∪C1S3）
6．函数f(x)=x3+ax2+3x－9，已知f(x)=在x=－3时取得极值，则a= （ ）
A．2 B．3 C．4 D．5
7．设b>0，二次函数y=ax2+bx+a2－1的图像为下列之一
 |
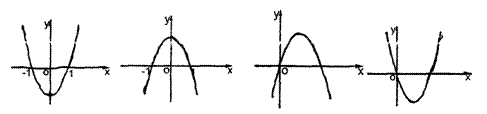则a的值为 （ ）
A．1 B．－1 C．
D．
8．设0<a<1，函数f(x)=loga(a2x－2ax－2)，则使f(x)<0的x的取值范围是 （ ）
A．(－∞,0) B．(0,+ ∞) C．(－∞,loga3) D．(loga3,+∞)
9．“m=
”是“直线(m+2)x+3my+1=0与直线(m－2)x+(m+2)y－3=0相互垂直”的（ ）
A．充分必要条件 B．充分而不必要条件
C．必要而不充分条件 D．既不充分也不必要条件
10．在R上定义运算
：xy=x(1－y).若不等式(x－a) (x+a)<1对任意实数x成立，则
A．－1<a<1 B．0<a<2 C．
D．
11．若函数
内单调递增，则a的取值范围
是 （ ）
A．
B．
C．
D．
12．计算机中常用十六进制是逢16进1的计数制，采用数字0~9和字母A~F共16个计数符
号，这些符号与十进制的数的对应关系如下表：
| 十六进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 十进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
例如：用十六进制表示：E+D=1B，则A×B=
A．6E B．72 C．5F D．B0
二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上。
13．曲线y=2x－x3在点（1，1）处的切线方程为 .
14．设y=f(x)是定义在R上的奇函数，且y=f(x)的图象关于直线x=对称，则
f(1)+f(2)+f(3)+f(4)+f(5)= .
15．若对任意x∈（－1，1），恒有2x2+(a+1)x－a(a－1)<0，则a的取值范围是 .
16．若等比数列{an}的公比大于1，且a7a11=6, a4+a14=5,则
.
三、解答题：本大题共6小题，共74分。解答应写出文字说明，证明过程或演算步骤。
17．（本大题满分12分）
记函数f(x)=
的定义域为A，g(x)=lg[(x－a－1)(2a－x)](a<1)的定义域为B。
（1）求A；
（2）若BA，求实数a的取值范围。
18．（本大题满分12分）
已知函数
（1）求此函数的定义域，并判断该函数的单调性
（2）解关于x的不等式
19．（本小题满分12分）
已知函数f(x)=ax3+cx+d(a≠0)是R上的奇函数，当x=1时f(x)取得极值－2.
（1）求f(x)的单调区间和极大值；
（2）证明对任意x1，x2∈（－1，1），不等式f(x1)－f(x2)<4恒成立。
20．（本小题满分12分）
已知数列{log2(an－1)}(n∈N*)为等差数列，且a1=3, a3=9
（1）求数列{an}的通项公式；
（2）证明
21．（本小题满分12分）
已知函数f(x)和g(x)的图像关于原点对称，且f(x)=x2+2x
（1）求函数g(x)的解析式；
（2）解不等式g(x)≥f(x)－x－1
22．（本小题满分14分）
已知函数
（1）求函数f(x)的反函数f－1(x)
（2）若不等式
对于区间
上的每个x的值都成立，求实数m的取值范围。
数学试卷（文）参考答案
一、选择题
1~5 DDABC 6~10 DBCBC 11~12 BA
二、填空题：
13．x+y－2=0 14．0 15．a≥3或a≤－1 16．
三、解答题：
17．（1）A={xx≥5或x<1} （2）a≤0
18．（1）定义域（－1，1）， f(x)在（－1，1）上为减函数
（2）
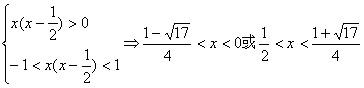
∴解集为
19．（1）d=0.
∴x∈(－∞,－1)上f(x)
x∈(1，+∞)上f(x)
∴x∈(－1, 1)上f(x)
f(x)极大值f(－1)=2
（2）x∈(－1, 1)上f(x)↓ ∴f(x)<f(－1)=2.
f(x)>f(1)= －2.
∴x1x2∈(－1,1) f(x1)－f(x2)<f(－1)－f(1)=4
20．（1）令bn=log2(an－1).
（2）
21．（1）设g(x)上一点（x, g(x)）其关于（0，0）的对称点（－x, －g(0)在f(x)上 .
∴－g(x)=(－x)2－2x ∴g(x)=2x－x2
（2）g(x)≥
解集为[－1，].
22．（1）
（2）原不等式
