旧州中学2005~2006学年度第二学期高三年级第二次月考
数学试题
学号 姓名 班级 得分
一、选择题：（每小题5分，10个小题共50分）
1、函数
的定义域为（
）
A、
B、（-2，1） C、
D、
2、
是
的（ ）条件
A、充分 B、必要 C、充要 D、不充分也不必要
3、在
的展开式中
的系数为（
）
A、-20 B、20 C、-15 D、15
4、在下列函数中，偶函数是（ ）
A、
B、
C、
D、
5、设
，方程
的解为( )
A、
B、
C、
D、
6、
、
、
是平面，
、
、
是直线，则下列命题中正确的是（ ）
A、若∥，
，则∥ B、若∥，∥，则∥
C、若⊥，
，则∥ D、若∥，
，则∥
7、某天上午要排语文、数学、电脑、体育四节课，其中体育不排在第一节，则不同的排法有（ ）种
A、6 B、9 C、18 D、21
8、若
，则下列不等式中正确的为（ ）
A、
B、
C、
D、
9、理:命题“若
与
共轭,则
”的逆否命题是( )
A、若,则=
B、若
,则
C、若,则 D、若,则=
（文）有A、B、C三种零件分别为a个，300个，b个。分层从中抽取容量为45的样本，抽取了A为20个，C为10个，则a=（ ）
A、200 B、400 C、600 D、1200
10、已知抛物线的顶点在原点，焦点为（-1，0）则抛物线的方程为（ ）
A、
B、
C、
D、
二、填空题：（每小题4分，10个小题共40分）
11、方程
的解为
12、若
，
，则
=
13、
的图象与x轴无交点，B：
恒成立，A或B真，则a的范围是
14、理：
（文）：不等式
的解集为
15、理：若
为虚数单位，则
=
（文）：
则
16、函数
的最大值为
17、正三棱锥P-ABC的底面边长为6cm，侧棱和底面成
角，则其体积为
18、理：若
，则
（文）若
，则方程
有 个正整数解
19、已知A(2,0)、B（0，2），则以AB为直径的圆的方程为
20、在10件产品中有2件是次品，现从中任取3件，则取得恰有一件次品的概率为
三、解答题：（本大题有7个小题，共60分）
21、（7分）数列
为等差数列，若
，求该数列的前10项之和
22、（7分）若
，
且
，求
的最大值。
23、（7分）已知
，
，求
24、（9分）若
，
，求向量
与
的夹角
25、（10分）四棱锥V-ABCD的底面为矩形，侧棱VA⊥面ABCD
（1）求证：面VCD⊥面VAD；
（2）若VA=AB=a，AD=2a，求异面直线AB和VC所成的角。
26、(10分)已知
，求
的极值
27、(10分)等腰直角三角形APB的一直角边AP在y轴上，A位于x轴下方，B位于y轴右方，斜边AB的长为
，且A、B在C：
上。
（1） 若P（0，1），求、b；（2）若P（0，t），求t的取值范围
附参考答案:
一、1C2A3D4B5C 6B7C8B9B10C
二、11、x=1,12、
,13、
,14、理:0;文: 
,15、理: 0 ；文： 72 16、 1 17、
18、理：6
；文：
19、
20、
三、
21、由已知，得：
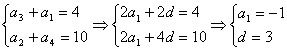
22、u的最大值为11。提示：由已知条件作出可行域，由目标函数易知，欲使u取得最大值，则x应取最小值而y取最大值，从而可得可行解为（0，4）
23、由，得：
，
∴
24、由，得：
，
∴
∴
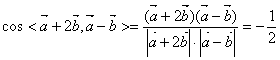
25、（1）利用三垂线定理先证CD⊥VD，从而可证得CD⊥面VAD，又根据线面垂直判定定理，可得面VCD⊥面VAD
（2）因为CD∥AB，所以∠VCD即为所求角，在Rt△VAD中，由勾股定理可求出VD=
，所以在Rt△VCD中，有：
，从而
26、由得：
令
(1)当a>0时, 不等式
,此时可知: 
为极大值点；
为极小值点，所以
；
(2)当a<0时, 
,
27、(1)由题意,可设点P(x,1),则易知:
,b=3-1=2,从而有:
(2)同(1) 设点P(x,t),则易知:,b=3-t>0,从而有
t<3, 
又a>b,所以 
