泸州市高中2006级第二次教学质量诊断性考试
数 学（理工农医类）
本试卷分第I（选择题）和第II卷（非选择题）两部分. 第I卷1至2页，第II卷3至8页. 共150分. 考试时间120分钟.
第I卷（选择题 共60分）
注意事项：
1．答第I卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
2．每小题选出答案后，用铅笔把答题卡对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上。
3．考试结束，监考人将本试卷和答题卡一并收回。
参考公式：
如果事件A、B互斥，那么 如果事件A在一次试验中发生的
P(A+B)=P(A)+P(B) 概率是p，那么n次独立重复试验
如果事件A、B相互独立，那么 中恰好发生k次的概率
P(A·B)=P(A)·P(B)
一．选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。
(1)已知全集U=R，集合A={x(x+2)(x-1)<0}, B={x-1≤x<2}，则A∩(CU B)为
(A) {xx<-2, 或x>1} (B) {xx<-2, 或x≥0}
(C) {x-2<x<-1} (D) {xx<-1, 或x>1}
(2)抛物线y2=12x的准线方程为
(A) x=3 (B) x=-3 (C) y=3 (D) y=-3
(3)设向量a=(-1, 2), b=(1, -1), c=(3, -2)，若c=λ1a+λ2b，则实数λ1, λ2的值为
(A) λ1=4, λ2=1 (B) λ1=1, λ2=4
(C) λ1=0, λ2=4 (D) λ1=1, λ2=-4
(4)若a>1时，则
的最小值为
(A) 2 (B) 3 (C) 4 (D) 5
(5)设z=a+bi, 
且
，则
的值为
(A) i (B) –i (C) 1-i (D)1+i
(6)在等比数列
中，
，则
(A)
(B)
(C)
(D)
(7)设正态函数
，则下列命题不正确的是
(A)总体的平均数为10
(B)函数f (x)的曲线是关于直线x=10对称
(C)函数f (x)的曲线与x轴有交点
(D)总体的标准差为2
(8)已知变量x、y满足下列条件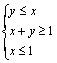
，则目标函数z=2x+y的最小值为
(A) 3 (B)
(C)
2 (D)
(9)若sin
则cos
=
(A) 
(B)
(C)
(D)
(10)已知F1、F2是椭圆的两个焦点，过F1且与椭圆长轴垂直的直线交椭圆于A、B两点，若∆ABF2是正三角形，则这个椭圆的离心率是
(A) 
(B)
(C)
(D)
(11)称集合A的非空真子集的真子集叫做集合A的“孙子集”，则集合A={a, b, c, d, e}的孙子集共有
(A) 11个 (B) 39个 (C) 26个 (D) 10个
(12)设函数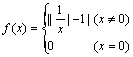
，则关于x的方程f 2(x)+bf
(x)+c=0有7个不同实数解的充要条件是
(A) -1<b<0且c>0 (B)b>0且c>0
(C) -1<b<0且c=0 (B)b≥0且c=0
泸州市高中2006级第二次教学质量诊断性考试
数 学（理工农医类）
第II卷（非选择题 共90分）
注意事项：(1)用钢笔或圆珠笔直接答在试题卷中。(2)答题前将密封线内的项目填写清楚。
| 题号 | 二 | 三 | 总分 | 总分人 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 分数 | |||||||||
| 得分 | 评卷人 |
二．填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上。
(13)二项式
的展开式中含
的项的系数为_____________.
(14)
= _____________.
(15)抛物线的顶点是双曲线16x2-9y2=144的中心，焦点是双曲线的左顶点，则该抛物线方
程是_____________.
(16)已知函数f (x)的导函数
的图像如图所示，给出以下结论：
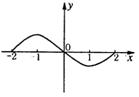①函数f (x)在(-2, -1)和(1, 2)上是单调递增函数；
②函数f (x)在(-2, 0)上是单调递增函数，在(0, 2)上是单调递减函数；
③函数f (x)在x=-1处取得极大值，在x=1处取得极小值；
④函数f (x)在x=0处取得极大值f (0).
则正确命题的序号是__________（填上所有正确命题的序号）
三．解答题：本大题共6小题，共74分. 解答应写出文字说明、证明过程或演算步骤.
| 得分 | 评卷人 |
（17）（本小题满分12分）
若
(I)求f (x)的最小正周期；
(II)记g(x)=2f (x)+a
的最小值为-2，求实数a的值.
| 得分 | 评卷人 |
(18)（本小题满分12分）
已知圆C的参数方程为
(θ为参数，且θ∈[0, 2π))，且圆C与直线l1: x+y-1=0的两个交点为P、Q，若
（O为坐标原点）.
(I)求实数a的值；
(II)若a≠0，直线l2与l1有相同的方向向量，且截圆C所得弦长是1，求直线l2的方程.
| 得分 | 评卷人 |
(19)（本小题满分12分）
甲、乙两个独立地破译一个密码，甲能译出的概率为
，乙能译出的概率为x，甲、乙两人中至少有一人能译出的概率为y，恰有一人能译出的概率为
.
(I)求x, y的值；
(II)求甲、乙两人都译不出的概率.
| 得分 | 评卷人 |
(20)（本小题满分12分）
已知函数
，数列{an}的首项为
，前n项和为sn，且当n≥2时，sn=f (sn-1).
(I)证明：数列
是等差数列，并求出sn的表达式；
(II)设
，求数列{bn}的前n项和Tn.
| 得分 | 评卷人 |
(21)（本小题满分12分）
已知函数
上为增函数.
(I)求实数a的取值范围；
(II)设f (x)的导函数为f ′(x), g(x)=sinx+cosx-1, a取（1）中的最小值，求证：当x>0时，g(x)>f ′(x).
| 得分 | 评卷人 |
(22)（本小题满分14分）
已知两点M(-2, 0), N(2, 0)，动点P在y轴上的射影是H，若存在常数m使
，m+2, m
成等差数列.
(I)求动点P的轨迹C的方程；
(II)当m∈[-4, 0]时，讨论动点P的轨迹是什么图形？
(III)当m=-2时，过点N的直线l交曲线C于x轴下方两个不同点A、B，设R为AB中点，若过点R与点Q(0, -2)的直线交x轴于点D(x0, 0)，求x0的取值范围.
