江苏省六合高级中学高二（下）数学周周练C卷（3）
一、选择题：
1、.给出下列命题，其中正确的两个命题是
①直线上有两点到平面的距离相等，则此直线与平面平行 ②夹在两个平行平面间的两条异面线段的中点连线平行于这两个平面 ③直线m⊥平面α，直线n⊥m，则n∥α ④a、b是异面直线，则存在唯一的平面α，使它与a、b都平行且与a、b距离相等 （ ）
A.①② B.②③ C.③④ D.②④
2、在直二面角
中，等腰直角三角形
的斜边
，一直角边
，
与
所成角的正弦值为
，则
与所成的角是
（ ）
（A）
（B）
（C）
（D）
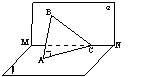
（第2题图）
3、如图，已知面ABC⊥面BCD，AB⊥BC，BC⊥CD，且AB=BC=CD，设AD与面ABC所成角为
，AB与面ACD所成角为β，则与β的大小关系为
（ ）
（A）＜β
（B）=β （C）＞β
（D）无法确定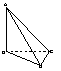
4、.在正方形SG1G2G3中，E、F分别是G1G2、G2G3的中点，D是EF的中点，沿SE、SF及EF把这个正方形折成一个四面体，使G1、G2、G3三点重合，重合后的点记为G，那么，在四面体S—EFG中必有 （ ）
A.SG⊥平面EFG B.SD⊥平面EFG C.FG⊥平面SEF D.GD⊥平面SEF
5、在三棱锥A—BCD中，若AD⊥BC，BD⊥AD，△BCD是锐角三角形，那么必有 （ ）
A.平面ABD⊥平面ADC B.平面ABD⊥平面ABC
C.平面ADC⊥平面BCD D.平面ABC⊥平面BCD
6、如图，正方体ABCD－A1B1C1D1的棱长为1，E是A1B1的中点，则E到平面AB C1D1
的距离为 （ ）
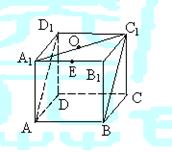A．
B．
C．
D． 
二、填空题：
7、设a、b是异面直线，α、β是两个平面，且a⊥α，b⊥β，a
β，bα，则当__________（填上一种条件即可）时，有α⊥β.
8、夹在互相垂直的两个平面之间长为2a的线段和这两个平面所成的角分别为45°和30°，过这条线段的两个端点分别向这两个平面的交线作垂线，则两垂足间的距离为_____________.
9、△ABC的三个顶点A、B、C到平面α的距离分别为2 cm、3 cm、4 cm，且它们在α的同侧，则△ABC的重心到平面α的距离为_____________.
三、解答题：
10、在四棱锥P—ABCD中，底面ABCD是矩形，AB=2，BC=a，又侧棱PA⊥底面ABCD.
（1）当a为何值时，BD⊥平面PAC?试证明你的结论.
（2）当a=4时，求证：BC边上存在一点M，使得PM⊥DM.
（3）若在BC边上至少存在一点M，使PM⊥DM，求a的取值范围.
11、如下图，四棱锥P—ABCD的底面是边长为a的正方形，PA⊥底面ABCD，E为AB的中点，且PA=AB.
（1）求证：平面PCE⊥平面PCD；
（2）求点D到平面PCE的距离.
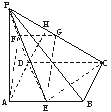
12、如下图，在四棱锥P—ABCD中，底面ABCD是∠DAB=60°，且边长为a的菱形，侧面PAD为正三角形，其所在的平面垂直于底面ABCD.
（1）若G为AD边的中点，求证：BG⊥平面PAD；
（2）求证：AD⊥PB；
（3）求二面角A—BC—P的大小；
（4）若E为BC边的中点，能否在棱PC上找一点F，使得平面DEF⊥平面ABCD，并证明你的结论.
江苏省六合高级中学高二（下）数学周周练C卷（3）答案卷
一、选择题：
1、.给出下列命题，其中正确的两个命题是
①直线上有两点到平面的距离相等，则此直线与平面平行 ②夹在两个平行平面间的两条异面线段的中点连线平行于这两个平面 ③直线m⊥平面α，直线n⊥m，则n∥α ④a、b是异面直线，则存在唯一的平面α，使它与a、b都平行且与a、b距离相等
A.①② B.②③ C.③④ D.②④
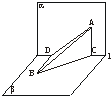
解析：①错误.如果这两点在该平面的异侧，则直线与平面相交.②正确.如下图，平面α∥β，A∈α，C∈α，D∈β，B∈β且E、F分别为AB、CD的中点，过C作CG∥AB交平面β于G，连结BG、GD.
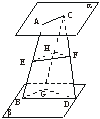
设H是CG的中点，则EH∥BG，HF∥GD.
∴EH∥平面β，HF∥平面β.
∴平面EHF∥平面β∥平面α.
∴EF∥α，EF∥β.
③错误.直线n可能在平面α内.
④正确.如下图，设AB是异面直线a、b的公垂线段，E为AB的中点，过E作a′∥a，b′∥b，则a′、b′确定的平面即为与a、b都平行且与a、b距离相等的平面，并且它是唯一确定的.
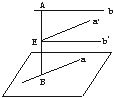
答案：D
2、在直二面角中，等腰直角三角形的斜边，一直角边，与所成角的正弦值为，则与所成的角是
（A）
（B）
（C）
（D）
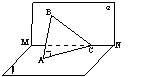
（第2题图）
3、如图，已知面ABC⊥面BCD，AB⊥BC，BC⊥CD，且AB=BC=CD，设AD与面ABC所成角为，AB与面ACD所成角为β，则与β的大小关系为
（A）＜β （B）=β （C）＞β
（D）无法确定
4、.在正方形SG1G2G3中，E、F分别是G1G2、G2G3的中点，D是EF的中点，沿SE、SF及EF把这个正方形折成一个四面体，使G1、G2、G3三点重合，重合后的点记为G，那么，在四面体S—EFG中必有
A.SG⊥平面EFG B.SD⊥平面EFG C.FG⊥平面SEF D.GD⊥平面SEF
解析：注意折叠过程中，始终有SG1⊥G1E，SG3⊥G3F，即SG⊥GE，SG⊥GF，所以SG⊥
平面EFG.选A. 答案：A
5、在三棱锥A—BCD中，若AD⊥BC，BD⊥AD，△BCD是锐角三角形，那么必有
A.平面ABD⊥平面ADC B.平面ABD⊥平面ABC
C.平面ADC⊥平面BCD D.平面ABC⊥平面BCD
解析：由AD⊥BC，BD⊥AD
AD⊥平面BCD，面AD
平面ADC，
∴平面ADC⊥平面BCD. 答案：C
6、如图，正方体ABCD－A1B1C1D1的棱长为1，E是A1B1的中点，则E到平面AB C1D1
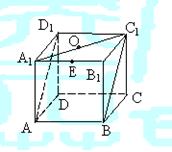的距离为
（ B ）
A． B．
C． D．
二、填空题：
7、设a、b是异面直线，α、β是两个平面，且a⊥α，b⊥β，aβ，bα，则当__________（填上一种条件即可）时，有α⊥β.
解析：本题为开放性问题.可以填上a⊥b，也可以填a∥β，或b∥α. 答案：a⊥b
8、夹在互相垂直的两个平面之间长为2a的线段和这两个平面所成的角分别为45°和30°，过这条线段的两个端点分别向这两个平面的交线作垂线，则两垂足间的距离为_____________.
解析：如下图，平面α⊥β，α∩β=l，A∈α，B∈β，AB=2a.
AC⊥l于点C，BD⊥l于点D，则CD即为所求.∵α⊥β，AC⊥l，∴AC⊥β，
∠ABC就是AB与平面β所成的角.故∠ABC=30°，故AC=a. 同理，
在Rt△ADB中求得AD=
a.在Rt△ACD，CD=
=a.答案：a
9、△ABC的三个顶点A、B、C到平面α的距离分别为2 cm、3 cm、4 cm，且它们在α的同侧，则△ABC的重心到平面α的距离为_____________.
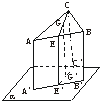
解析：如下图，设A、B、C在平面α上的射影分别为A′、B′、C′，△ABC的重心为G，连结CG交AB于中点E，又设E、G在平面α上的射影分别为E′、G′，则E′∈A′B，G′∈C′E，EE′=
（A′A+B′B）=
，CC′=4，CG∶GE=2∶1，
在直角梯形EE′C′C中可求得GG′=3.答案：3 cm
三、解答题：
10、在四棱锥P—ABCD中，底面ABCD是矩形，AB=2，BC=a，又侧棱PA⊥底面ABCD.
（1）当a为何值时，BD⊥平面PAC?试证明你的结论.
（2）当a=4时，求证：BC边上存在一点M，使得PM⊥DM.
（3）若在BC边上至少存在一点M，使PM⊥DM，求a的取值范围.
分析：本题第（1）问是寻求BD⊥平面PAC的条件，即BD垂直平面PAC内两相交直线，易知BD⊥PA，问题归结为a为何值时，BD⊥AC，从而知ABCD为正方形.
解析：（1）解：当a=2时，ABCD为正方形，则BD⊥AC.
又∵PA⊥底面ABCD，BD平面ABCD，
∴BD⊥PA.∴BD⊥平面PAC. 故当a=2时，BD⊥平面PAC.
（2）证明：当a=4时，取BC边的中点M，AD边的中点N，连结AM、DM、MN.
∵ABMN和DCMN都是正方形，
∴∠AMD=∠AMN+∠DMN=45°+45°=90°，即DM⊥AM.又PA⊥底面ABCD，由三垂线定理得，PM⊥DM，故当a=4时，BC边的中点M使PM⊥DM.
（3）解：设M是BC边上符合题设的点M，∵PA⊥底面ABCD，∴DM⊥AM.
因此，M点应是以AD为直径的圆和BC边的一个公共点，则AD≥2AB，即a≥4为所求.
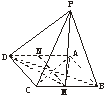
11、如下图，四棱锥P—ABCD的底面是边长为a的正方形，PA⊥底面ABCD，E为AB的中点，且PA=AB.
（1）求证：平面PCE⊥平面PCD；
（2）求点D到平面PCE的距离.
解析：（1）证明：取PD的中点F，则AF⊥PD.
∵CD⊥平面PAD，∴AF⊥CD.
∴AF⊥平面PCD.
取PC的中点G，连结EG、FG，可证AFGE为平行四边形.
∴AF∥EG.∴EG⊥平面PCD.
∵EG在平面PCE内，∴平面PCE⊥平面PCD.
（2）解：在平面PCD内，过点D作DH⊥PC于点H.
∵平面PCE⊥平面PCD，∴DH⊥平面PCE，即DH为点D到平面PCE的距离.
在Rt△PAD中，PA=AD=a，PD=a.
在Rt△PCD中，PD=a，CD=a，PC=
a，∴DH=
=
a.
12、如下图，在四棱锥P—ABCD中，底面ABCD是∠DAB=60°，且边长为a的菱形，侧面PAD为正三角形，其所在的平面垂直于底面ABCD.
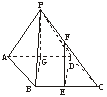
（1）若G为AD边的中点，求证：BG⊥平面PAD；
（2）求证：AD⊥PB；
（3）求二面角A—BC—P的大小；
（4）若E为BC边的中点，能否在棱PC上找一点F，使得平面DEF⊥平面ABCD，并证明你的结论.
解析：（1）证明：∵在菱形ABCD中，∠DAB=60°，G为AD边的中点，∴BG⊥AD.又平面PAD⊥平面ABCD，平面PAD∩平面ABCD=AD，∴BG⊥平面PAD.
（2）证明：连结PG，则PG⊥AD，由（1）得BG⊥AD，又PG∩BG=G，BG平面PBG，PG平面PBG，∴AD⊥平面PBG，PB平面PBG.∴AD⊥PB.
（3）解：由（2）AD⊥平面PBG，而BC∥AD，∴BC⊥平面PBG.而PB平面PBG，BG平面PBG，∴BC⊥PB，BC⊥BG.∴∠PBG就是二面角A—BC—P的平面角.
在△PAD中，PG=
a，∴在△PGB中，∠PBG=45°，即二面角A—BC—P为45°.
（4）解：当F为PC的中点时，满足平面DEF⊥平面ABCD.证明如下：
取PC的中点F，连结DE、EF、DF，则由平面几何知识，在△PBC中，EF∥PB，在菱形ABCD中，GB∥DE，而EF平面DEF，ED平面DEF，EF∩DE=E，∴平面DEF∥平面PGB.又PG⊥平面ABCD，而PG平面PGB，∴平面PGB⊥平面ABCD.故平面DEF⊥平面ABCD.