江苏省六合高级中学高三年级阶段性考试试卷04.11
数 学
命题人：刘 明
一、选择题（每题5分，共60分）
1．已知集合
Z｝，
Z｝，则
（ ）
A．M＝N
B．M
N
C．NM
D．
2．设
是三个任意的非零向量，且互不平行，以下四个命题：
①
；
②
；
③若
的夹角为
，则
表示向量
在向量
方向上的射影长；
④若
R），则向量
所成角为钝角的充要条件是
．
其中真命题的个数为 （ ）
A．1 B．2 C．3 D．4
3．函数
的反函数是
（ ）
A．
B．
C．
D．
4．函数
的奇偶性为
（ ）
A．奇函数 B．偶函数
C．既不是奇函数，又不是偶函数 D．既是奇函数，又是偶函数
5．已知
，则
等于
（ ）
A．0
B．0，或
C．
D．0，或－
6．设函数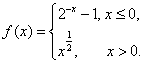
若
，则x0的取值范围是
（ ）
A．（－1，1） B．（－1，+∞）
C．（－∞，－2）∪（0，+∞） D．（－∞，－1）∪（1，+∞）
7．某等比数列的前7项和是48，前14项和为60，则前21项的和是 （ ）
A．63 B．75 C．108 D．180
8．若
，则下列结论不正确的是
（ ）
A．
B．
C．
D．
9．方程
的根的情况是
（ ）
A．有4个不等的正根 B．有4个根，其中两个正根、两个负根
C．有两个异号根 D．有两个不等的正根
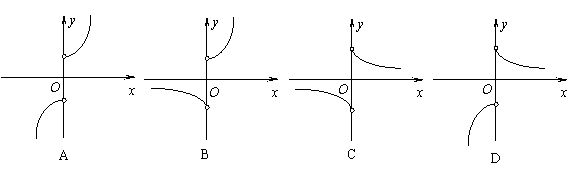
10．函数
的图像大致形状是
（ ）
11．若将函数
的图像按向量
平移，使图象上点
的坐标由
变为
则平移后的图像的解析式为
( )
A．
B．
C．
D．
12．函数
的单调递减区间是
（ ）
A．
Z）
B．
Z）
C．
Z）
D．
Z）
二、填空题（每题4分，共16分）
13． 函数
的值域是
．
14．方程
R）有一个正根和一个负根的充分不必要条件是
（只需写出一个符合条件的答案即可）．
15．将y＝
的图象作其关于直线y＝x的对称图象后得到图象C1，再作C1关于y轴对称的图象后得到图象C2，再将C2的图象向右平移1个单位得到图象C3，最后再作C3关于原点对称的图象得到C4，则C4所对应的函数的解析表达式是
．
16．给出下列命题：
①存在实数
，使得
；
②函数
是奇函数；
③将函数
的图像向左平移
个单位，得到函数
的图像；
④在
中，
．
其中正确命题的序号为 ．
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
13 ；14 ；15 ；16 ．
三、解答题（17～21题每题12分，22题14分，共74分．解答应写出文字说明、证明过程和演算步骤．）
17．已知
，
是两个不共线的向量，且
，
．
（Ⅰ）求证：
与
垂直；
（Ⅱ）若
，
，且
，求
的值．
18．已知等差数列
，公差大于
，且
是方程
的两根，数列
前
项和
．
（Ⅰ）写出数列、的通项公式；
（Ⅱ）记
，求证：
．
19．已知
．
（Ⅰ）若
的定义域为R, 求值域；
（Ⅱ）在区间
上是不是单调函数？证明你的结论；
（Ⅲ）设
，若对于
在集合
中的每一个值，在区间
上恰有两个不同的值与之对应，求集合.
20．工厂统计资料显示，产品次品率p与日产量n (件)
N＋，且
的关系表如下：
| n | 1 | 2 | 3 | 4 | ┅ | 98 |
| p |
|
|
|
| ┅ | 1 |
又知每生产一件正品盈利a元，每生产一件次品损失
元（
）.
(Ⅰ)将该厂日盈利额
（元）表示为日产量n (件)的一种函数关系式；
（Ⅱ）为了获得最大盈利，该厂的日产量应定为多少件？
21．已知点
都在直线
上，
为直线
与轴的交点，数列
成等差数列，公差为1. （
N＋）
(Ⅰ)求数列，
的通项公式；
(Ⅱ)若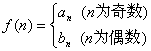
， 问是否存在
N＋，使得
成立；若存在，求出
的值，若不存在，说明理由.
(Ⅲ)求证：
…… +
(
2, N＋)
22．定义在（-1，1）上的函数
满足：
①对任意x，
（-1，1）都有
；
②当
（-1，0）时，
．
（Ⅰ）判断在（-1，1）上的奇偶性，并说明理由；
（Ⅱ）判断函数在（0，1）上的单调性，并说明理由；
（Ⅲ）若
，试求
的值．
参考答案：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | A | B | A | C | D | A | D | C | B | C | B |
13．
14．
可以取小于0的任意一个数） 15．
16．②④
17、解：(Ⅰ)（解法一）
……………………………………………２分
＝
…………………………………４分
与垂直．……………………………………………６分
（解法二）
……………………………………２分
……………………………４分
与垂直．……………………………………………………６分
(Ⅱ) 
．
． ………………………………………………………９分
…………………………12分
18．（Ⅰ）由题意得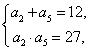
所以
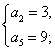或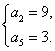
……………2分
又因为等差数列
的公差大于零，所以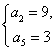
不合题意，舍去．
由
，得
．
．
………………………………………4分
由，得
……………………5分
当
，
……………6分
……………………………………………7分
．
……………………………………………………………8分
（Ⅱ）
，
………………………………………9分
．
…………11分
．
………………………………………………………12分
19.(Ⅰ)
–2
, ……………3分
所以，值域为
…………………………5分
（Ⅱ）在区间上不是单调函数 ．
……………………………7分
证明：∵ 
, 且
，
∴ 在区间上不是单调函数．
…………………………………9分
（Ⅲ）
或
． ……………………………………………12分
20．解（Ⅰ）由题意可知
N＋） …………………………1分
日产量n 件中，正品为
件，
………………………………3分
次品为
件
………………………………………4分
所以，日盈利额
N＋）. ………………………… 6分
注：未写出正确的定义域扣1分．
(Ⅱ)
………………………8分
． …………………………………………… 9分
当且仅当
即
时去取最大值， …………10分
N＋，且
，故
时，取最大值，即
取最大值. ……12分
21．(Ⅰ) 
.
…………………………………3分
(Ⅱ)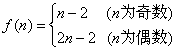 
假设存在符合条件的
(ⅰ)若为偶数，则
为奇数，有
，如果
，则
与为偶数矛盾.不符舍去；
(ⅱ) 若为奇数，则为偶数，有
这样的也不存在.
综上所述：不存在符合条件的.……………………………………… 7分
(Ⅲ) 
，
．………9分
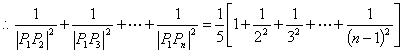………10分
．
……………………12分
22.（Ⅰ）令
．
…………………………2分
令y＝-x，则
在（-1，1）上是奇函数．…… 4分
（Ⅱ）设
，则
，…………6分
而
，
．
……………………8分
．即 当
时，
．
∴ f（x）在（0，1）上单调递减． …………………………………10分
（Ⅲ）由于
，
，
，
∴ 
．
…………………………………14分