江苏省南通市2005—2006学年度高三年级九校第一次联考
数学试卷
本试卷分第I卷(选择题)和第II卷(非选择题),满分150分,考试时间120分钟.
第I卷(选择题,共60分)
一、选择题:(每小题5分,共60分)
1、已知角![]() 的终边经过点
的终边经过点![]() ,且
,且![]() ,则
,则![]() 的值是( )
的值是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2、![]() 为等比数列,且
为等比数列,且![]() ,则
,则![]() ( )
( )
A、5 B、10 C、15 D、20
3、已知数列![]() 中,
中,![]() ,则
,则![]() =( )
=( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4、![]() ( )
( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
5、![]() 的结果是( )
的结果是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
6、设![]() 若
若![]() ,则
,则![]() 的值为( )
的值为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
7、在数列![]() 中,
中,![]() ,
,![]() ,则
,则![]() ( )
( )
A、1
B、![]() C、
C、![]() D、
D、![]()
8、设集合![]() 有且只有一个元素,则
有且只有一个元素,则![]() 的取值范围是( )
的取值范围是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
9、函数![]() 的图象与函数
的图象与函数![]() 的图象关于直线
的图象关于直线![]() 对称,则
对称,则![]() 的单调递增区间是( )
的单调递增区间是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
10、设![]() ,则
,则![]() 的充分不必要条件是( )
的充分不必要条件是( )
A、![]() B、
B、![]() 或
或![]() C、
C、![]() D、
D、![]()
11、函数![]() ,若
,若![]() 时,
时,
![]() 则( )
则( )
A、![]() B、
B、![]() C、
C、![]() D、无法确定
D、无法确定
12、有限数列![]() :
:![]() 为其前
为其前![]() 项和,定义
项和,定义![]() 为
为![]() 的“凯森和”,若有99项的数列
的“凯森和”,若有99项的数列![]() 的“凯森和”为1000,则有100项的数列
的“凯森和”为1000,则有100项的数列![]() 的“凯森和”为( )
的“凯森和”为( )
A、1001 B、991 C、999 D、990
第II卷(非选择题,共90分)
二、填空题:(每小题4分,共24分)
13、已知![]() 的一条对称轴方程为
的一条对称轴方程为![]() ,则
,则![]() 的值为_______________;
的值为_______________;
14、若![]() 为锐角,且
为锐角,且![]() ,则
,则![]() 的值是___________________;
的值是___________________;
15、函数![]() 的图象和直线
的图象和直线![]() 围成的一个封闭的图形面积是__________;txjy
围成的一个封闭的图形面积是__________;txjy
16、若![]() ,则
,则![]() ______________________;
______________________;
17、已知数列![]() 的前项和
的前项和![]() ,则
,则![]() 的值为_______;
的值为_______;
18、已知数列![]() 满足
满足![]() 且
且![]() ,则
,则![]() ________________;
________________;
三、解答题:(共66分)
19、已知:![]() ⑴求
⑴求![]() ;⑵求
;⑵求![]() 的值。
的值。
20、已知![]() ,
,![]() ,求
,求![]() 的值。
的值。
21、已知函数![]()
⑴当![]() 时,求
时,求![]() 的单调递增区间;⑵当
的单调递增区间;⑵当![]() 时,且
时,且![]() 的最小值为2,求
的最小值为2,求![]() 的值。
的值。
22、已知正项数列![]() 的前
的前![]() 项和满足
项和满足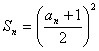 ,
,![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() 。
。
23、已知一次函数![]() 的反函数为
的反函数为![]() ,且
,且![]() ,若点
,若点![]() 在曲线
在曲线![]() 上,
上,![]() 对于任意
对于任意![]() ,均有
,均有![]()
⑴求![]() 的解析式;
的解析式;
⑵求![]() ;
;
⑶求![]() 。
。
参考答案及评分标准:
一、选择题:(每小题5分,共60分)
1~6:AACADA 7~12:ADDDBB
二、填空题:(每小题4分,共24分)
13、![]() 14、
14、![]() 15、
15、![]() 16、
16、![]() 17、67
18、
17、67
18、![]()
三、解答题:
19、本大题12分
解:⑴![]()
![]() ---------------4分
---------------4分
⑵![]() ----------------10分
----------------10分
 -----------12分
-----------12分
20、本大题12分
解:![]() ------------------------3分
------------------------3分
![]() --------8分
--------8分
∴![]()
--------------------10分
![]() ---------------------12分
---------------------12分
21、本大题14分
解: ⑴![]()
![]() --------------------------3分
--------------------------3分
由![]() ,
,![]() 得:
得:![]() -----------6分
-----------6分
∴![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() ---------------------------------------8分
---------------------------------------8分
⑵∵![]()
∴![]() -
------------------------------------10分
-
------------------------------------10分
∴![]() --------------------------------------12分
--------------------------------------12分
∴![]() 的最小值为
的最小值为![]() ∴
∴![]() =2
-------------------------------14分
=2
-------------------------------14分
22、本大题14分
解:当![]() 时,
时,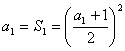 ,解得:
,解得:![]() -------------------------------------1分
-------------------------------------1分
当![]() 时,
时,
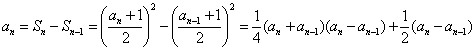
即:![]() -------------------------4分
-------------------------4分
∵![]() 为正项数列 ∴
为正项数列 ∴![]() ∴
∴![]() ------------------------------6分
------------------------------6分
∴![]() 为首项为1,公差为2的等差数列。
为首项为1,公差为2的等差数列。
∴![]() ---------------------------8分
---------------------------8分
∴![]()
当![]() 为偶数时:
为偶数时:
![]()
![]()
![]()
![]()
![]() ------11分
------11分
当![]() 为奇数时:∵
为奇数时:∵![]() 为奇数∴
为奇数∴![]() 为偶数
为偶数
∴![]()
![]()
综上所述:
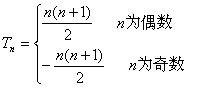 -------------------------------------------14分
-------------------------------------------14分
23、本大题14分
解:⑴∵![]() ∴
∴![]() ----------①
----------①
∵一次函数![]() 的反函数为
的反函数为![]()
∴不妨设![]() ∵
∵![]() ∴
∴![]() ∴
∴![]() -----------------2分
-----------------2分
∵点![]() 在曲线
在曲线![]() 上
上
∴![]() -----------------------------②
-----------------------------②
由①②得:![]()
∴![]() -------------------------------------------------------5分
-------------------------------------------------------5分
⑵∵对于任意![]() ,均有
,均有![]()
∴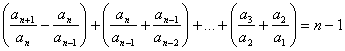
∴![]()
∵![]() ,
,![]() ∴
∴![]() ∴
∴![]()
∴![]()
∴![]() ----------------------------------------10分
----------------------------------------10分
⑶∵![]()
∴![]() =
=![]()
=![]()
![]() ----------------------------------------14分
----------------------------------------14分