江苏省如皋中学高三年级调研考试试卷

江苏省如皋中学高三年级05届调研考试试卷05.04

数　 学

一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1、已知集合A={0，，2}，集合B={α，β，γ}，映射f：A→B，则满足的象是α的不同映射有

A、3个　　　　　  B、6个　　　　　　 C、8个　　　　　　  D、9个

2、若不等式2x－3>4与不等式x²+px+q>0的解集相同，则=

A、　　　　　　 B、　　　　　　 C、　　　　　　 D、

3、一个容量为20的样本数据，分组后，组距与频数如下：，2；，3；，4；，5；，x；，2。则样本在上的频率为

A、　　　　　　 B、　　　　　　  C、　　　　　　　 D、

4、已知函数在区间(－∞，+∞)上是减函数，则a的取值范围是

A、a>　　　　　  B、0<a<　　　　  C、c<　　　　　　 D、<a<1

5、已知点A(－1，0)，B(1，0)，以AB为一腰作使∠DAB=90⁰的直角梯形ABCD，且AD=3BC，CD中点的纵坐标为1，若椭圆以A、B为焦点且过点D，则此椭圆方程为

A、　　　　　　　　　　　　 B、

C、　　　　　　　　　　　　 D、

6、如果三位数的十位数字既大于百位数字也大于个位数字，则这样的三位数一共有

A、240个　　　　　 B、285个　　　　  C、231个　　　　　  D、243个

7、如果以原点为圆心的圆经过双曲线（a>0，b>0）的焦点，且被该双曲线的右准线分成弧长为2:1的两段圆弧，那么该双曲线的离心率e等于

A、　　　　　  B、　　　　　 C、　　　　　 　D、

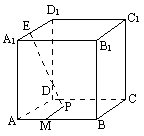8、正方体ABCD—A₁B₁C₁D₁的棱长为1，点M在棱AB上，且AM=，点P是平面ABCD上的动点，且点P到直线A₁D₁的距离与点P到点M的距离的平方差为1，则点P的轨迹是

A、抛物线

B、双曲线

C、直线

D、圆

9、若α、β是两个平行平面，其中α上有4个点，β上有3 个

点，从中任取5个点，则能构成四棱锥的最大概率是

A、　　　　　　 B、　　　　　　 C、　　　　　  D、

10、若ab<0，且a+b=1，二项式(a+b)⁹按a的降幂展开后，其第二项不大于第三项，则实数a的取值范围为

A、(－∞，0)　　　　　　　　　　　　 B、，+∞)

C、(－∞，　　　　 　　　　　　　 D、(1，+∞)

11、已知f(x)是定义在R上的偶函数，且对任意x∈R都有f(x－1)=f(x+3)，当x∈[4，6]时，f(x)=2^x+1，则f(x)在区间[－2，0]上的反函数f^—1(x)的值f^—1(19)为

A、log₂15　　　　　　　　　　　　　  B、3－2log₂3

C、5+log₂3　　　　　　　　　　　　　 D、－1－2log₂3

12、在棱长为2R的无盖立方体容器内装满水，先将半径为R的球放入水中，然后再放入一个球，使它完全浸入水中，要使溢出的水量最大，则此球的半径是

A、R　　　　　　　　　　　  B、R

C、R　　　　　　　　　　　  D、R

第Ⅱ卷（共90分）

二、填空题：本大题共4小题，共16分，把答案写在题中的横线上。

13、已知函数f(x)=Acos²(ωx+)+1（A>0，ω>0）的最大值为3，f(x)的图象在y轴上的截距为2，其相邻两对称轴间的距离为2，则f(1)+f(2)+f(3)+…+f(100)=____________

14、已知a>0，b>0，且关于x的方程x²+ax+2b=0与方程x²+2bx+a=0都有实数根，则a+b的最小值为_________________

15、设{a_n}为等差数列，且a₁=p，a_n+1=q，

则=________________________

16、设函数f(x)的定义域为R，若存在常数M>0，使得f(x)≤Mx对一切实数x均成立，则称f(x)为F函数，给出下列函数：

①f(x)=0；　　 ②f(x)=x²；　　 ③f(x)=(sinx+cosx)；　　④f(x)=；

⑤f(x)是定义在R上的奇函数，且对于任意实数x₁，x₂，均有f(x₁)－f(x₂)≤2x₁－x₂。

则其中是F函数的序号是____________________

三、解答题：本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤。

17、（本小题满分12分）

口袋里装有大小相同的卡片八张，其中三张标有数字1，三张标有数字2，二张标有数字3。

（1）从口袋中任取两张卡片，求抽得相同数字的概率。

（2）从口袋中任取一张卡片记下数字，放回口袋后再任取一张，记两次取得卡片数字之和为A，问A为何值时，其发生的概率最大？说明理由。

18、（本小题满分12分）

设，

（1）如果x∈R，恒有，求α的值。

（2）若sin2α= 且f(x)= +2cosα，f(x)的最大值为0，求cosα的值。

19、（本小题满分12分）

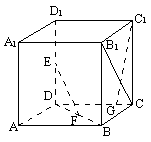
已知在正方体ABCD—A₁B₁C₁D₁中，E、F分别是D₁D、BD的中点，G在棱CD上。

（1）求证：EF⊥B₁C；

（2）若EF与C₁G所成角的余弦值为，试确定G点的位置；

（3）在（2）的结论下，求二面角F—EG—G的大小（用反三角函数表示）。

20、（本小题满分12分）

已知函数F(x)=2x－t－x³+x+1（x∈R，t为常数，t∈R）

（1）写出此函数F(x)在R上的单调区间；

（2）若方程F(x)－k=0恰有两解，求实数k的值。

21、（本小题满分12分）

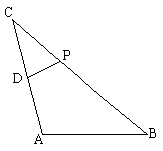
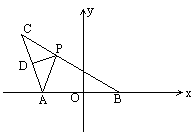
如图，已知=2c，=2a（a>c）且，=0，（C为动点）。

（1）建立适当的平面直角坐标系，求出点P的轨迹方程；

（2）若点P的轨迹上存在两个不同的点E、F，且线段EF的中垂线与AB（或AB的延长线）相交于一点Q，求出点Q的活动范围。

22、（本小题满分14分）

（1）记S_n、T_n分别为下列两个等差数列的前n项和。

{a_n}：5，3，1，－1，－3，－5，－7，…

{b_n}：－14，－10，－6，－2，2，6，10，14，18，…

计算S₁，S₂，S₄，S₅及T₁，T₃，T₅，T₇，并根据计算结果，对于存在正整数k，满足a_k+a_k+1=0的一类等差数列{a_n}的和的规律，猜想一个正确的结论并证明你的结论。

（2）对于公差为d（d≠0）的等差数列{a_n}，求证：数列中不同的两项之和仍是这个数列中一项的充要条件是存在整数m≥－1，使得a₁=md。

附：参考答案

一、选择题

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案	D	A	D	B	C	A	D	A	D	A	B	C

二、填空题

13、　　　200　　 　　　　　　　14、　　 6　　　　　 

15、　 (p+q)2^n—1　 　　　　　　　16、　 ①④⑤　  

三、解答题

17、解：（1）从口袋中任取两张卡片，共有种方法

若两张卡片数字相同，共有种方法

∴ 抽得相同数字的概率 P=

（2）两个数字之和A的值为2，3，4，5，6

　　 ∵ A=2的概率 P₁=

　　　　A=3的概率 P₂=

　　　　A=4的概率 P₃=

　　　　A=5的概率 P₄=

　　　　A=6的概率 P₅=

　　 ∴ 当A=4时，其发生的概率最大

18、解：（1）由题意，

sin(α－x)－sin(α+x)=0

∴ cosα·sinx=0

　　　　 又 ∵ x∈R，∴ cosα=0

∴ （k∈Z）

（2）f(x)=－2cosαsinx+2cosα

　　　  =2cosα(1－sinx)

　　 ∵ f(x)的最大值为0

　　 ∴ cosα<0

　　　又 sin2α=2sinαcosα>0

　　　∴ sinα<0

　　　∴

　　　cos2α<0　得cos2α=

　　　∴ cosα=

19、解：（1）连接D₁B、BC₁

∵ E、F是D₁D、BD的中点

∴ EF//D₁B　 且EF=D₁B

又∵ D₁C₁⊥平面BC₁

∴ D₁B在平面BC₁上的射影为BC₁

∵ BC₁⊥B₁C，由三垂线定理知B₁C⊥D₁B

∴ EF⊥B₁C

（2）延长CD至点P，使得DP=CG

　　 连接D₁P、PB

　　 ∴ D₁C₁PG

　　 ∴ 四边形D₁C₁GP为平行四边形

　　 由（1）知　EF//D₁B

　　 ∴ ∠PD₁B为异面直线EF与C₁G所成的角

　　 设正方体的棱长为4，CG=t （0≤t≤4）

　　 则D₁P²=16+t²，D₁B²=48，PB²=16+(4+t)²

　　 则

　　 解得　t=1

　　 ∴ 点G是棱CD接近于点C的四等分点

（3）取CD的中点M，连接FM，则FM⊥CD

　　 过M作MN⊥EG交于N点，连接FN

　　 则FN⊥EG

　　 ∴ ∠MNF的补角为二面角F-EG-C₁的平面角

　　 设正方体棱长为4，在Rt△MNG中

　　 MN=

　　 在Rt△FMN中，∠FMN=90⁰

　　 ∴ tan∠MNF=

　　 ∴ 二面角F-EG-C₁的大小为

20、解：（1）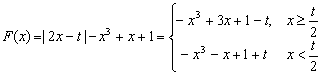

∴

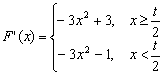
由－3x²+3=0 得x₁=－1，x₂=1，而－3x²－1<0恒成立

∴ i) 当<－1时，F(x)在区间(－∞，－1)上是减函数

　　 在区间(－1，1)上是增函数，在区间(1，+∞)上是减函数

ii) 当1>≥－1时，F(x)在区间(－∞，)上是减函数

　 在区间(，1)上是增函数，在区间(1，+∞)上是减函数

iii) 当≥1时，F(x)在(－∞，+∞)上是减函数

　　　　（2）由1）可知

i) 当<－1时，F(x)在x=－1处取得极小值－1－t，

在x=1处取得极大值3－t，若方程F(x)－m=0恰有两解，

此时m=－1－t或m=3－t

ii) 当－1≤<1，F(x)在x=处取值为，

在x=1处取得极大值3－t，若方程F(x)－m=0恰有两解，

此时m=或m=3－t

iii) 当≥1时，不存在这样的实数m，使得F(x)－m=0恰有两解

21、解：（1）如图，以A、B所在直线为x轴，AB的中垂线为y轴

建立平面直角坐标系，由题设，2，

∴

而

∴ 点P是以A、B为焦点，

长轴长为2a的椭圆

即

（2）设E(x₁，y₁)，F(x₂，y₂)，Q(x₀，0)

　　 x₁≠x₂，

　　 即(x₁－x₀)²+y₁²=(x₂－x₀)²+y₂²（*）

　　 又E、F在轨迹上

　　 ∴ ，

　　 将y₁²、y₂²代入（*）式整理，得

　　

　　 ∵ x₁≠x₂　　∴

　　 －a≤x₁≤a　 －a≤x₂≤a

　　 －2a<x₁+x₂<2a

　　 ∴ 　　即

　　 ∴ 点Q在与AB中点相距的线段上活动（不包括两端点）

22、解（1）S₁=5，S₂=8，S₄=8，S₅=5

　　　　　 T₁=－14，T₃=－30，T₅=－30，T₇=－14

　　　　　 对于等差数列{a_n}，当a_k+a_k+1=0时

　　　　　 猜想：S_n=S_2k—n（n≤2k，n、k∈N*）

　　　　　 证明：设等差数列{a_n}的首项为a₁，公差为d

　　　　　 ∵ a_k+a_k+1=0，∴ 2a₁=(1－2k)d

　　　　　 又S_2k—n－S_n=(2k－n)a₁+

=

=0

　　　　　 ∴ S_n=S_2k—n成立

（2）证明：必要性

　　 任取等差数列{a_n}中不同的两项a_p、a_q（p≠q）

　　 若存在k，使得a_p+a_q=a_k

　　　　　 则2a₁+(p+q－2)d=a₁+(k－1)d

　　　　　 得a₁=(k－p－q+1)d

　　　　　 ∴ 存在整数m=k－p－q+1使得a₁=md

　　　　　 下面用反证法证明m≥－1

　　　　　 对于d≠0，若m<－1，则取t=－m≥2

　　　　　 对于数列中的两项a₁，a_t，存在a_s

　　　　　 使得a₁+a_t=a_s

　　　　　 即有　2md+(－m－1)d=md+(s－1)d

　　　　　 得sd=0，这与s>0，d≠0产生矛盾

　　　　　 故m≥－1

　　　　　 充分性

　　　　　 若存在m≥－1，使得a₁=md

　　　　　 对于不同的正整数s，t，有s+t≥3

　　　　　 ∴ s+t+m≥2且a_s+a_t=2a₁+(s+t－2)d

=a₁+(m+s+t－2)d=a_m+s+t－1

　　　　　 即存在第m+s+t－1项恰好等于a_s+a_t

　　　　　 综合以上，命题得证