江苏省苏大附中2006年4月数学模拟考试
第I卷(共50分)
一、选择题:(本大题12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.定义在R上的函数y=f(x)的值域为[a,b],则f(x+1)的值域为 ( )
(A)[a,b] (B)[a+1,b+1] (C)[a-1,b-1] (D)无法确定
2.条件![]() ,条件
,条件![]() ,则
,则![]() 是
是![]() 的
( )
的
( )
(A)充分非必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要的条件
3.一个物体的运动方程是![]() ,其中
,其中![]() 的单位是米,
的单位是米,![]() 的单位是秒,那么物体在3秒末的瞬时速度是
( )
的单位是秒,那么物体在3秒末的瞬时速度是
( )
(A)7米/秒 (B).6米/秒 (C)5米/秒 (D)8米/秒
|
|
5.10个人抽2张球票,一人一次依次抽取(每抽一次不放回),则第k个人抽到球票的概率(k=1,2,…,10)为 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
6.Sn是等差数列{an}的前n项和,若a2+a4+a15是一个确定的常数,则数列{Sn}中是常数的项为 ( )
(A)S7 (B)S8 (C)S13 (D)S11
7.为了得到函数![]() 的图象,可以把函数y=lgx的图象 ( )
的图象,可以把函数y=lgx的图象 ( )
(A)向上平移一个单位
![]() (B)向下平移一个单位
(B)向下平移一个单位
(C)向左平移一个单位 (D)向右平移一个单位
8.若![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() 的大小关系是( )
的大小关系是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
9.若![]() , A
, A![]() ,G
,G![]() ,H
,H![]() ,其中
,其中![]() ,
,![]() R+,则A,G,H的大小关系是
( )
R+,则A,G,H的大小关系是
( )
(A)A≤G≤H (B)A≤H≤G (C)H≤G≤A (D)G≤H≤A
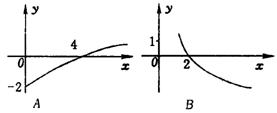
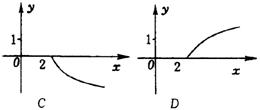
10.已知函数![]() 图象如图甲,则
图象如图甲,则![]() 在区间[0,
在区间[0,![]() ]上大致图象是( )
]上大致图象是( )
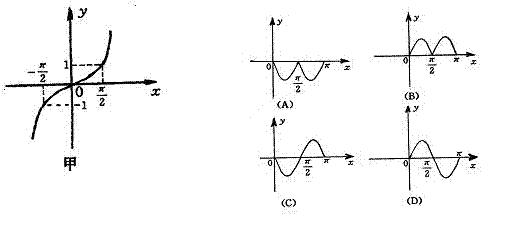 |
第Ⅱ卷(非选择题 共90分)
二、填空题(每小题5分,共30分.)
11.
|
12.若函数y=f(x)的图象关于点![]() 为对称时,则
为对称时,则
f(-3)+f(-2)+f(-1)+f(0)+f(1)+f(2)+f(3)+f(4)= .
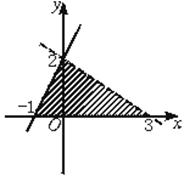
13.如图,表示图中平面区域的公共区域的不等式组是__________.
14.有A、B、C、D、E五名学生参加数学竞赛,决出了从第一到第五的名次,A、B两位同学去问成绩,老师对A说:“你没能得第一名”。又对B说:“你是第三名”,从这个问题分析,这五个个人的名次排列共有 种可能(用数字作答)。
15.已知函数![]() ,若数列
,若数列![]() 成等差数列,则非零常数
成等差数列,则非零常数![]() 、
、![]() 的一组值可以是
的一组值可以是![]() ___,
___,![]() __ (写出一组满足条件的
__ (写出一组满足条件的![]() 、
、![]() 值即可)
值即可)
16.设![]() 是任意非零的平面向量,且互不共线,给出下面的五个命题:
是任意非零的平面向量,且互不共线,给出下面的五个命题:
(1)![]() ; (2)
; (2)![]() 不与向量
不与向量![]() 垂直.;
垂直.;
(3)![]() ;
(4)若
;
(4)若![]() ,则
,则![]() ,或者
,或者![]() ;
;
(5)![]() ; (6)
; (6)![]()
其中真命题的序号为____________________________.
三、解答题:(本大题6个小题,共66分必需写出必要的文字说明、推理过程或计算步骤).
17.(本小题满分12分)
甲、乙2人分别对一目标射击1次,甲射中的概率为0.8,乙射中的概率为0.9,求:
(1)2人都射中的概率;
(2)2人中恰有1人射中的概率;
(3)2人至少有1 人射中的概率.
 |
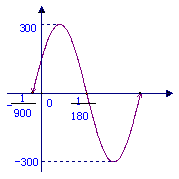
18.(本小题满分12分)
已知电流I与时间t的关系式为![]() .
.
(1)右图是![]() (ω>0,
(ω>0,![]() )
)
在一个周期内的图象,根据图中数据求![]()
的解析式;
(2)如果t在任意一段![]() 秒的时间内,电流
秒的时间内,电流![]() 都能取得最大值和最小值,那么ω的最小正整数值是多少?
都能取得最大值和最小值,那么ω的最小正整数值是多少?
19.(本小题满分14分)
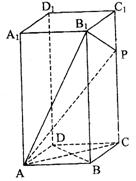
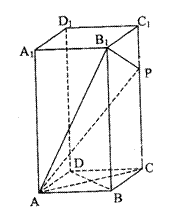
在正四棱柱ABCD—A1B1C1D1中,侧棱是底面边长的2倍,P是侧棱CC1上的一点.
(1)求证:不论P在侧棱CC1上何位置,总有BD⊥AP;
(2)若CC1=3C1P,求平面AB1P与平面ABCD所成的二面角;
|
20.(本小题满分14分)
定义:称![]() 为
为![]() 个正数
个正数![]() 的“均倒数”。已知数列
的“均倒数”。已知数列![]() 的前
的前![]() 项的“均倒数”为
项的“均倒数”为![]() ,(1)求
,(1)求![]() 的通项公式;(2)设
的通项公式;(2)设![]() ,试判断并说明
,试判断并说明![]() 的符号;(3)设函数
的符号;(3)设函数![]() ,是否存在最大的实数
,是否存在最大的实数![]() ,当
,当![]() 时,对于一切正整数
时,对于一切正整数![]() ,都有
,都有![]() 。
。
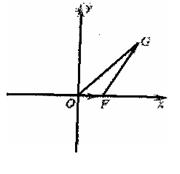
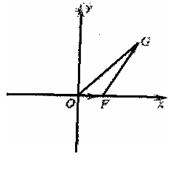 21.(本小题满分14分)
21.(本小题满分14分)
以O为原点,![]() 所在直线为x轴,建立如图所示的直角坐标系.设
所在直线为x轴,建立如图所示的直角坐标系.设![]() 点F的坐标为(t,0),
点F的坐标为(t,0),![]() ,点G的坐标为
,点G的坐标为![]() (1)求
(1)求![]() 关于t的函数
关于t的函数![]() 的表达式,判断函数
的表达式,判断函数![]() 的单调性,并证明你的判断.(2)设△OFG的面积
的单调性,并证明你的判断.(2)设△OFG的面积![]() ,若以O为中心,F为焦点的椭圆经过点G,求当
,若以O为中心,F为焦点的椭圆经过点G,求当![]() 取得最小值时椭圆的方程.
取得最小值时椭圆的方程.
(3)在(2)的条件下,若点P的坐标为![]() ,C、D是椭圆上的两点,且
,C、D是椭圆上的两点,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
 江苏省苏大附中2006年3月数学模拟考试
江苏省苏大附中2006年3月数学模拟考试
高三数学答卷纸
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二.填空题:(每题5分,共50分)
| 11. 12. 13. 14. 15. ,. 16. |
三.解答题
| 17.(本小题满分14分)
18.(本小题满分14分) | ||||||||
|
20.(本小题满分14分) 21.(本小题满分14分)
| ||||||||
22.(本小题满分14分) |
评分标准及参考答案
一、1.A 2.A 3. C 4. C 5.B 6.C 7.B 8. C 9. A 10. D
二、11.15 12. -4 13.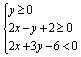 14. 18 15.
14. 18 15. ![]() ,
,![]() 16. (3),(6)_
16. (3),(6)_
三、17.(14分)
解析:设“甲射击1次,击中目标”为事件A,“乙射击1次,击中目标”为事件B,则A与B, ![]() 与B,A与
与B,A与![]() ,
,![]() 与
与![]() 为相互独立事件.
为相互独立事件.
(1)2人都射中的概率为
![]()
(2)2人恰有1人射中包括甲中乙不中、甲不中乙中2种情况,其对应事件为互斥事件.
![]()
(3)法一:2人至少有1人射中包括“2人都中”和“2人有1人不中”2种情况,其概率为:
![]()
法二:“2人都未击中”的概率为
![]() .
.
“2人中至少有1人击中”与“2人都未击中” 为对立事件.
所以“两人至少有1人击中”的概率为![]() 14分
14分
18.(14分)解:(1)由图可知 A=300,设t1=-![]() ,t2=
,t2=![]() ,
,
则周期T=2(t2-t1)=2(![]() +
+![]() )=
)=![]() .∴ ω=
.∴ ω=![]() =150π.
=150π.
又当t=![]() 时,150π·
时,150π·![]() +
+![]() =π,∴
=π,∴ ![]() =
=![]() .
.
故所求的解析式为![]() .
.
(2)依题意,周期T≤![]() ,即
,即![]() ≤
≤![]() ,(ω>0)
,(ω>0)
∴ ω≥300π>942,又ω∈N*,故最小正整数ω=943. 14分
19.(14分)解:向量法(1)略 (2)![]()
(3)P距C1距离是底面边长的![]() 倍. 14分
倍. 14分
20 (14分) 解:(1)![]() ,
,![]()
两式相减,得 ![]() ,
,![]()
(2)![]() ,
,
![]() 。
。
(3)由(2)知 ![]() 是数列
是数列![]() 中的最小项,∵
中的最小项,∵![]() 时,对于一切自然数
时,对于一切自然数![]() ,都有
,都有![]() ,即
,即![]() , ∴
, ∴![]() ,即
,即![]() ,解之,得
,解之,得 ![]() ,∴取
,∴取 ![]() 。
。
21.解:(1)由题意知:![]()
解得![]()
设![]()
=![]()
∵![]() ∴
∴![]()
函数![]() 在区间[3,+∞)上单调递增.
在区间[3,+∞)上单调递增.
(2)由![]()
∴点G的坐标为![]()
∵函数![]() 在区间[3,+∞]上单调递增,
在区间[3,+∞]上单调递增,
∴当t=3时,![]() 取得最小值,此时点F、G的坐标分别为
取得最小值,此时点F、G的坐标分别为
(3,0)、(![]() ).
).
由题意设椭圆方程为![]()
由点G在椭圆上,得![]() 解得b2=9.
解得b2=9.
∴所求椭圆方程为![]()
(3)解答一:设C、D的坐标分别为(x,y)、(m,n),
则![]()
由![]()
∵点C、D在椭圆上,∴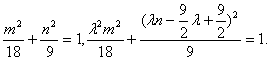
消去m,得![]()
又∵![]() ∴
∴![]()
∴实数λ的取值范围是![]()
解答二:设点A、B的坐标分别为(0,3)、(0,-3),过点A、B分别作y轴的垂线,交直线PC于点M、N.
若![]() ∴1
∴1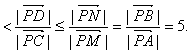
则![]()
若![]() 同理可得
同理可得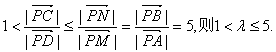 综上,实数λ的取值范围是
综上,实数λ的取值范围是![]()
 19.(本小题满分14分)
19.(本小题满分14分)