江苏省苏州市田家炳实验中学高三年级第二次综合测验
数学试卷（理）
全卷共150分。考试用时120分钟。
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。
第Ⅰ卷（选择题 共50分）
一、选择题:本大题共10小题，每小题5分，共50分。在每个小题给出的四个选项中，只有一项是符合题目要求的。
1．设集合
，
，则
等于
A．
B．
C．
D．
2．在复平面内，复数
对应的点位于
（A）第一象限 （B）第二象限 （C）第三象限 （D）第四象限
3.下列四个命题中真命题是
①“若xy=1，则x、y互为倒数”的逆命题 ②“面积相等的三角形全等”的否命题 ③“若m≤1，则方程x2－2x+m=0有实根”的逆否命题 ④“若A∩B=B，则A
B”的逆否命题
A.①② B.②③ C.①②③ D.③④
4、集合
的子集的个数是
A. 无穷多 B. 32 C.
16
D. 8
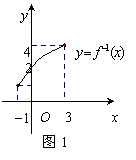
5．函数
的反函数
的图像与
轴交于点
（如图1所示），则方程
在
上的根是
A.4 B.3 C. 2 D.1
6．设
，则
的定义域为
A．
B．
C．
D．
7.已知定义在R上的奇函数f(x)满足f(x+2)=－f(x),则,f(6)的值为
(A)－1 (B) 0 (C) 1 (D)2
8．对于R上可导的任意函数f（x），若满足（x－1）
³0，则必有
A． f（0）＋f（2）<2f（1） B. f（0）＋f（2）£2f（1）
C. f（0）＋f（2）³2f（1） D. f（0）＋f（2）>2f（1）
9.等差数列
, 
的前n 项之和分别为Sn 和Tn
,若
,则
等于
A. 1 B. 
C.
D. 
10.为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则为:明文a,b,c,d对应密文a+2b,2b+c,2c+3d,4d,例如,明文1,2,3,4对应密文5,7,18,16.当接收方收到密文14,9,23,28时,则解密得到的明文为
A.4,6,1,7 B.7,6,1,4 C.6,4,1,7 D.1,6,4,7
第Ⅱ卷（非选择题 共100分）
注意事项：第Ⅱ卷用0.5毫米黑色的签字笔或黑色墨水钢笔直接答在答题卡上。答在试题卷上无效。
二、填空题：本大题共5小题，每小题4分， 共20分，把答案填在答题卡相应位置上。
11.
_________.
12．设离散型随机变量
可能取的值为1，2，3，4。
（
1，2，3，4）。又的数学期望
，则
;
13.设
.
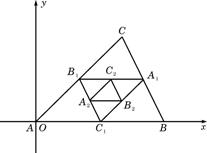14． 如图，连结△ABC的各边中点得到一个新的
△A1B1C1，又连结的△A1B1C1各边中点得到，如此无限继
续下去，得到一系列三角形：△ABC，△A1B1C1，△A2B2C2，…，
这一系列三角形趋向于一个点M，已知A(0,0) ,B(3,0),C(2,2)，
则点M的坐标是 .
15. 对于函数
，给出下列命题：①f (x)有最小值；②当a=0时，
f (x)的值域为R；③当a>0时，f (x)在区间
上有反函数；④若f (x)在区间
上是增函数，则实数a的取值范围是
. 上述命题中正确的是
(填上所有正确命题序号) .
三、解答题：本大题共6小题，共80分，解答应写出文字说明，证明过程或演算步骤。
16.（本小题满分12分）
已知函数
（1）当a=－1时，求函数f (x)的最大值和最小值.
（2）求实数a的取值范围，使
上是单调函数.
17.（本小题满分12分）
若
，
,
且
，其中Z为整数集,求实数
的取值范围。
18. （本小题满分14分）已知f (x)＝x
，
(1) 证明：f (x)>0；(2) 设F(x)＝f(x＋t)－f (x－t) (t≠o)，试判断F(x)的奇偶性。
19. （本小题满分14分）
统计表明，某种型号的汽车在匀速行驶中每小时耗油量y（升）关于行驶速度x（千米/小时）的函数解析式可以表示为：y=
(0<x≤120).已知甲、乙两地相距100千米。
（Ⅰ）当汽车以40千米/小时的速度匀速行驶时，从甲地到乙地要耗油多少升？
（Ⅱ）当汽车以多大的速度匀速行驶时，从甲地到乙地耗油最少？最少为多少升？
20. （本小题满分14分）
函数
的定义域为R，并满足以下条件：
①对任意
，有
；②对任意
、
，有
；③
（Ⅰ）求
的值；
（Ⅱ）求证：在R上是单调增函数；
（Ⅲ）若
，求证：
21. （本小题满分14分）
设
是定义在[－1，1]上的偶函数，，
的图象关于直线
对称，且当x
时，
（1）求的表达式；
（2）是否存在正实数，使函数的图象的最高点在直线
上，若存在，求出正实数的值；若不存在，请说明理由.
市田家炳实验中学高三年级第二次综合测验
数学试卷（理科）
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。 全卷共150分。考试用时120分钟。
第Ⅰ卷（选择题 共50分）
一、选择题:本大题共10小题，每小题5分，共50分散。在每个小题给出的四个选项中，只有一项是符合题目要求的。
1．（安徽卷）设集合，，则等于（ ）
A．
B．
C．
D．
解：
，
，所以
，故选B。
2．（北京卷）在复平面内，复数对应的点位于
（A）第一象限 （B）第二象限 （C）第三象限 （D）第四象限
解：
故选D
3.下列四个命题中真命题是
①“若xy=1，则x、y互为倒数”的逆命题 ②“面积相等的三角形全等”的否命题 ③“若m≤1，则方程x2－2x+m=0有实根”的逆否命题
④“若A∩B=B，则AB”的逆否命题
A.①② B.②③ C.①②③ D.③④
解析：写出满足条件的命题再进行判断.
答案：C
4、集合的子集的个数是 D
A. 无穷多 B. 32 C. 16 D. 8
5．（广东卷）函数的反函数的图像与轴交于点
（如图1所示），则方程在上的根是
A.4 B.3 C. 2 D.1
解：
的根是
2，故选C
6．（湖北卷）设，则的定义域为
A． B． C． D．
解：f（x）的定义域是（－2，2），故应有－2<
<2且－2<
<2解得－4<x<－1或1<x<4
故选B
7.（山东卷）已知定义在R上的奇函数f(x)满足f(x+2)=－f(x),则,f(6)的值为
(A)－1 (B) 0 (C) 1 (D)2
解：因为f（x）是定义在R上的奇函数，所以f（0）＝0，又f（x＋4）＝－f（x＋2）＝f（x），故函数，f（x）的周期为4，所以f（6）＝f（2）＝－f（0）＝0，选B
8．（江西卷）对于R上可导的任意函数f（x），若满足（x－1）³0，则必有（ C ）
B． f（0）＋f（2）<2f（1） B. f（0）＋f（2）£2f（1）
C. f（0）＋f（2）³2f（1） D. f（0）＋f（2）>2f（1）
解：依题意，当x³1时，f¢（x）³0，函数f（x）在（1，＋¥）上是增函数；当x<1时，f¢（x）£0，f（x）在（－¥，1）上是减函数，故f（x）当x＝1时取得最小值，即有f（0）³f（1），f（2）³f（1），故选C
9.等差数列, 的前n 项之和分别为Sn 和Tn ,若,
则等于
A. 1 B. C. D.
10.为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则为:明文a,b,c,d对应密文a+2b,2b+c,2c+3d,4d,例如,明文1,2,3,4对应密文5,7,18,16.当接收方收到密文14,9,23,28时,则解密得到的明文为(C )
A.4,6,1,7 B.7,6,1,4 C.6,4,1,7 D.1,6,4,7
第Ⅱ卷（非选择题 共100分）
注意事项：
第Ⅱ卷用0.5毫米黑色的签字笔或黑色墨水钢笔直接答在答题卡上。答在试题卷上无效。
二、填空题：本大题共5小题，每小题4分，(第15小题每空2分)共20分，把答案填在答题卡相应位置上。
11._________.
解：
。
12．（四川卷）设离散型随机变量可能取的值为1，2，3，4。（1，2，3，4）。又的数学期望，则 ;
解：设离散性随机变量可能取的值为
，所以
，即
，又的数学期望，则
，即
，
,∴ 
.
13.设
. 5
14．（福建卷）如图，连结△ABC的各边中点得到一个新的
△A1B1C1，又连结的△A1B1C1各边中点得到，如此无限继
续下去，得到一系列三角形：△ABC，△A1B1C1，△A2B2C2，…，
这一系列三角形趋向于一个点M，已知A(0,0) ,B(3,0),C(2,2)，
则点M的坐标是 .
解：如图，连结
的各边中点得到一个新的
又连结
的各边中点得到
，如此无限继续下去，得到一系列三角形：，，，
，这一系列三角形趋向于一个点M。已知
则点M的坐标是的重心，∴ M=
15. 对于函数，给出下列命题：①f (x)有最小值；②当a=0时，
f (x)的值域为R；③当a>0时，f (x)在区间上有反函数；④若f (x)在区间
上是增函数，则实数a的取值范围是. 上述命题中正确的是
(填上所有正确命题序号) . （15）②③
三、解答题：本大题共6小题，共80分，解答应写出文字说明，证明过程或演算步骤。
16.（本小题满分12分）
已知函数
（1）当a=－1时，求函数f (x)的最大值和最小值.
（2）求实数a的取值范围，使上是单调函数.
16．（本题满分12分）
解：（1）1，37 （2）
17.（本小题满分12分）
若，,
且，其中Z为整数集,求实数的取值范围。
解：．
，
（………………2分）
(1)当
时,
不符合题意.（…………………5分）
(2)当
时,
得
（……………………9分）
(3)当
时,
不符合题意。（…………………12分）
综上所得
（…………………14）
18. （本小题满分14分）
统计表明，某种型号的汽车在匀速行驶中每小时耗油量y（升）关于行驶速度x（千米/小时）的函数解析式可以表示为：y=(0<x≤120).已知甲、乙两地相距100千米。
（Ⅰ）当汽车以40千米/小时的速度匀速行驶时，从甲地到乙地要耗油多少升？
（Ⅱ）当汽车以多大的速度匀速行驶时，从甲地到乙地耗油最少？最少为多少升？
解：（I）当
时，汽车从甲地到乙地行驶了
小时，
要耗没
（升）。
答：当汽车以40千米/小时的速度匀速行驶时，从甲地到乙地耗油17.5升。
（II）当速度为
千米/小时时，汽车从甲地到乙地行驶了
小时，设耗油量为
升，
依题意得
令
得
当
时，
是减函数；
当
时，
是增函数。
当
时，取到极小值
因为在
上只有一个极值，所以它是最小值。
答：当汽车以80千米/小时的速度匀速行驶时，从甲地到乙地耗油最少，最少为11.25升。
19. （本小题满分14分）
已知f (x)＝x，
(1) 证明：f (x)>0；
(2) 设F(x)＝f(x＋t)－f (x－t) (t≠o)，试判断F(x)的奇偶性。
解：(1) 函数f (x)的定义域是{x x∈R且x≠0}, 且f (－x)＝(－x)·
＝f (x),
∴ f (x)是偶函数。当x>0时, 2x>1, 2x－1>0, ∴ f (x)>0,
当x<0时, －x>0, f (x)＝f (－x)>0, ∴ 对所有定义域内的x的值，都有f (x)>0.
(2) F(－x)＝f (－x＋t)－f (－x－t)＝f (x－t)－f (x＋t)＝－F(x), ∴ 函数是奇函数。
20. （本小题满分14分）
函数的定义域为R，并满足以下条件：
①对任意，有；
②对任意、，有；
③
（Ⅰ）求的值；
（Ⅱ）求证：在R上是单调增函数；
（Ⅲ）若，求证：
解法一：（1）令
，得：
（2）任取
、
，且
.设
则
在R上是单调增函数
（3）由（1）（2）知
而
解法二：（1）∵对任意x、y∈R，有
∴当
时
∵任意x∈R，
（2）
是R上单调增函数
即是R上单调增函数；
（3）
而
21. （本小题满分14分）
设是定义在[－1，1]上的偶函数，，的图象关于直线对称，且当
x时，
（1）求的表达式；
（2）是否存在正实数，使函数的图象的最高点在直线上，若存在，求出正实数的值；若不存在，请说明理由.
21、（I）当
时，上的点P（
与上的点Q（
关于对称，则
此时
代入
得
）
上是偶函数
当
时，
………………………………5分
（II）命题条件等价于
因为为偶函数，所以只需考虑
的情况.
求导
由
（舍）…………………………8分
①当0<
<1，即
时
|
| 0 | （0， |
| （ | 1 |
|
| + | — | |||
|
| 0 |
|
|
| －4+2 |
）
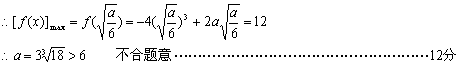
②当
，即
时，
上单调递增
综上，存在
使得的图象的最高点在直线上.……………14分