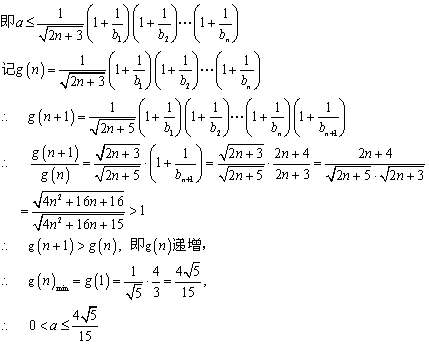江苏省宿迁市重点中学联考数学试题

江苏省宿迁市重点中学联考数学试题05.4

一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．某工厂生产A、B、C三种不同型号的产品，产品数量之比依次为，现用分层抽样方法抽出一个容量为的样本，样本中A种型号产品有16件.那么此样本的容量=　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　 （　　）

A．36　　　　　　 B．54　　　 　　　　　C． 72 　　　　　 D．144

2．在等差数列中，，，则该数列的前7项的和是

　　A.14　　　　　　  B.20　　　　　　 C.28　　　　　　  D.56

3．不等式的解集是　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 　　A． 　　　　　　　　　　　B．

　　　　　　　　　　　　　　　　　　　 C．　 　　　　　　　　　　　　　 D．

4．命题p：若a、b∈R，则a+b>1是a+b>1的充分而不必要条件；

　 命题q：函数y=的定义域是（－∞，－1∪[3，+∞.则　　　（　　）

　　　 A．“p或q”为假　　　　　　　　　　　　　　　　　B．“p且q”为真　

　　　 C．p真q假　　　　　　　　　　　　　　　　　　　　　D．p假q真

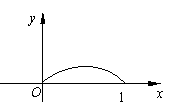5．已知函数f (x)（0≤x≤1）的图象的一段圆弧（如图所示）若，则（　 ）

A．　　  B.

C．　　  D．前三个判断都不正确

6．函数是偶函数，则函数的图象关于　　　　　　　　　  （　　）

　　　 A．直线x=2对称　　 B．直线x=－2对称　C．点（2，0）对称 D．点（－2，0）对称

7．双曲线的一条准线被它的两条渐近线所截得线段长度恰好等于它的一个焦点到一条渐近线的距离，则双曲线的离心率为　　　（　　）

　 A．3　　　　　  　　B．2　　　　　　　 C．　　　　　　 D．

8．已知正方体的棱长为a，以正方体的六个面的中心为顶点的多面体的表面积是　 （　　）

　　　 A．　　　　　　 B．　　　　　　　　 C． 　　　　　 D．

9．已知椭圆的左、右焦点分别为F₁、F₂，点P在椭圆上，若P、F₁、F₂是一个直角三角形的三个顶点，则点P到x轴的距离为　　　　　　　　　　  （　　）

A．4　　　　　　  B．　　　　  C． 　　　　 D．

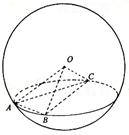
10．如图，A、B、C是表面积为48π的球面上三点，

AB=2，BC=4，∠ABC=60°，O为球心，则直线

OA与截面ABC所成的角是　　　　　　　　 （　　）

　　　 A．arcsin B．arccos

　　　 C．arcsin　　　　　　　　　D．arccos

11．已知函数满足：对任意实数，当时，总有则实数a的取值范围是　　　　　　　 （　　）

　A．（0，3）　　 　B．（1，3）　　　 　　 C．（2，2）　　　D．（1， 2）

12．在数列中，如果存在非零常数，使得对于任意的非零自然数均成立，那么就称数列为周期数列，其中叫数列的周期。已知数列满足，如果，当数列的周期最小时，该数列前2005项的和是　　　　　　　　　　　　　　　　　　　　　　　  （　　）

A．668　　　　　  B．669　　　　　　C．1336　　　　　  D．1337

二、填空题（本大题4个小题，每小题4分，共16分，只填结果，不要过程）

13．若的展开式中的常数项为84，则n=　　　　　　　  ．

14．有6个座位连成一排，现有3人就坐，则恰有两个空座位相邻的不同坐法有____种．

15．已知数列{a_n}满足：a₁＝14，a_n＋1＝a_n－（n∈N*），则使a_na_n＋2＜0成立的n的值是　　　　　　　　．

16．设x、y满足约束条件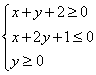，则z＝的最小值是_____，

的取值范围为________________________．

三、解答题（本大题6个小题，共74分，必需写出必要的文字说明、推理过程或计算步骤）

17．（12分）在中，是角所对的边，是该三角形的面积，且。

（Ⅰ）求角的度数；

（Ⅱ）若为锐角，，求的值。

18．（12分）甲乙两支球队经过加时赛比分仍为，现决定每队各派5名队员，每人射一个点球决定胜负。假设每名队员点球命中的概率均为（相互独立）。

（Ⅰ）如果不考虑乙球队，那么甲队5名队员中有连续三名队员射中，而另外两名队员未射中的概率是多少？

（Ⅱ）甲乙两队点球结束后，再次出现平局的概率是多少？

19．（12分）如图，在直三棱柱ABC—A₁B₁C₁中，∠ACB=90°，AC=BC=CC₁=1，M为AB的中点，A₁D=3DB₁.

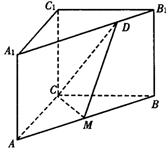
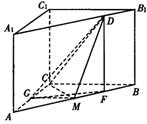
（Ⅰ）求证：平面CMD⊥平面ABB₁A₁；

（Ⅱ）求点A₁到平面CMD的距离；

（Ⅲ）求MD与B₁C₁所成角的大小.

20．（12分）对于函数

（Ⅰ）若函数在处的切线方程为，求、的值。

（Ⅱ）设是函数的两个极值点，且，证明：.

21．（12分）设分别为直角坐标平面内x，y轴正方向的单位向量，若向量且

（Ⅰ）求动点P（x，y）的轨迹方程；

（Ⅱ）已知点A（—1，0），设直线与点P的轨迹交于B，C两点，问是否存在实数m使得 ？若存在，求出m的值；若不存在，试说明理由。

22．（14分）已知正项数列中，，点在抛物线上；数列中，点在过点，以方向向量为的直线上。

（Ⅰ）求数列的通项公式；

（Ⅱ）若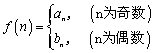，问是否存在，使成立，若存在，求出值；若不存在，说明理由；

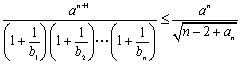（Ⅲ）对任意正整数，不等式成立，

求正数的取值范围．

参考答案：

CCADC 　 　ABBCD　　 DD

13．9　　14．72　　 15．21　　　16．,　[]

17．解：（Ⅰ）由已知等式得：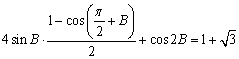

得　　

（Ⅱ）

18．（Ⅰ）记甲队5名队员中有连续三名队员射中，而另外两名队员未射中为事件A

则P（A）=

（Ⅱ）记甲乙两队点球结束后，再次出现平局为事件B，则P（B）=

答：（Ⅰ）甲队5名队员中有连续三名队员射中，而另外两名队员未射中的概率是。

（Ⅱ）甲乙两队点球结束后，再次出现平局的概率为。

19．解法一：（Ⅰ）（略）　

（Ⅱ）（方法一）在平面A₁B内，过A₁作A₁E⊥DM于E，

∵平面A₁B⊥平面CMD，则A₁E⊥平面CMD.

过D作DF⊥AB于F，∵∠A₁DE=∠DMF，

∠A₁ED=∠DFM=90°，∴△A₁ED∽△DFM，

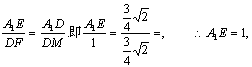∴∴A₁到平面CDM的距离为1.

（方法二）设A₁到平面CDM的距离为d，则　…6分

即 d=1.

（Ⅲ）取AC中点G，连结GM、GD，

∵

∴∠GMD或其补角即为异面直线MD与B₁C₁所成的角.

过D作DF⊥AB于F，则

连结GF，在△GAF中GF²=，

∴DG²=GF²+FD²=　∴

∴异面直线MD与B₁C₁所成的角为

20． 解：（Ⅰ）。

依题意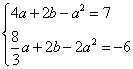得，解得

（Ⅱ）由是函数的两个极值点，

知是方程的两个根。所以，

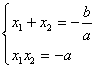　　  又因为，所以，异号，

所以，2＝＝。

即，其中。

设，则。

所以，在上单调递增，在单调递减。

所以，当时，

即，所以，。

方法二：。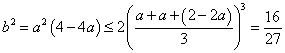

21.（Ⅰ）由得动点P（x，y）的轨迹方程

由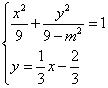　　得

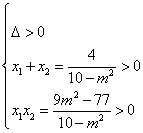则　得　

设 ，，

则

　　　　  =

把 ， 代入上式得：

　　 不存在

22．解：（Ⅰ）将点代入中得

（Ⅱ）

（Ⅲ）由