江苏省泰兴中学2004-2005学年度第二学期期中考试
高三数学
本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．共150分，考试时间120分钟．
第I卷 (选择题，共60分)
注意事项：
1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
2．选出答案后，用铅笔把答题卡上对应的题目的答案标号涂黑，如需改动，用橡皮擦干净后，再填涂其它答案，不能答在试卷上。
一、选择题（本题共12个小题，每小题5分，共60分。在每小题给出的四个选项中，有且只有一个是正确的）
1、已知全集
，集合
，
，则
为（ ）
A. 
B.
C.
D.
2、在
的展开式中含有常数项，则正整数n的最小值是（ ）
A. 4 B.
3、在
中，“
”是“
”的（ ）
A．充分而不必要条件 B．必要而不充分条件
C．充分必要条件 D．既不充分也不必要条件
4、已知斜三棱柱
中，底面是边长为1的正三角形，侧棱
，且
，
，则
与底面所成角的余弦值为（ ）
A. 
B. 
C. 
D. 
5、已知双曲线的中心在原点，离心率
，且它的一个焦点与抛物线
的焦点重合，则此双曲线的方程为（
）
A. 
B. 
C. 
D. 
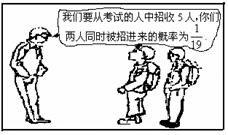6、两位同学去某大学参加自主招生考试，根据
右图学校负责人与他们两人的对话，可推断
出参加考试的人数为 （ ）
A. 19 B. 20 C. 21 D.22
7、用火柴棒按下图的方法搭三角形: （ ）
按图示的规律搭下去,则所用火柴棒数an 与所搭三角形的个数n之间的关系式可以是
A. 
B.
C.
D.
8、已知
，且
，给出下列式子：（ ）
①
，②
，③
，④
其中正确的是
A. ②③
B. ①④
C. ①③
D. ②④
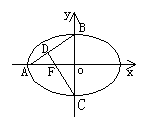
9、如图，椭圆中心在原点，离心率为，
为左焦点，
直线
与
交于点
,则
等于 （ ）
A．
B．
C．
D．
10、一小商贩准备用50元钱在一批发市场购买甲、乙两种小商品，甲每件4元，乙每件7元，甲商品每件卖出去后可赚1元钱，乙每件卖出去后可赚1.8元。若要使赚的钱最多，那么该商贩购买甲、乙两种商品的件数应分别为（ ）
A．甲7件，乙3件 B．甲9件，乙2件
C．甲4件，乙5件 D．甲2件，乙6件
11、已知函数
为奇函数，函数
为偶函数，且
，则
（ ）
| |
B. 
C.
D.
12、连续函数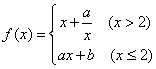
存在反函数，则实数b 的取值范围为（ ）
A .
B. 
C.
D.
第Ⅱ卷 (非选择题，共90分)
注意事项：
1．第Ⅱ共6页，用蓝、黑色的钢笔或圆珠笔直接答在试卷中。
2．答卷前，请将密封线内的项目填写清楚。
| 题号 | 二 | 三 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | |||
| 分数 | ||||||||
二、填空题：（本大题共4小题，每小题4分，共16分）
13、某单位业务人员、管理人员、后勤服务人员人数之比依次为
。为了了解该单位职员的某种情况，采用分层抽样方法抽出一个容量为
的样本，样本中业务人员人数为
，则此样本的容量
。
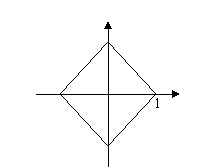
14、设P（x，y）是下图中四边形内的点或四边形边界上的点（即x、y满足的约束条件），
则
的最大值是__________。
15、在三角形ABC中，a、b、c分别是角A、B、C的对边，则
.类比到空间图形：在三棱锥
中，三个侧面PAB、PBC、PAC与底面
所成的角分别为
、
、
，相应的结论是___________________________.
16、若直线
与函数
，且
的图象有两个公共点，则
的取值范围是
．
三、解答题
17、（本小题12分）已知
，m为常数且m
-2,求使
成立的
的范围。
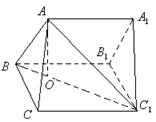18、（本小题12分）如图，已知三棱柱的底面ABC是直角三角形，
，侧棱
，
，且点A在平面
上的射影O在直线
上.
（Ⅰ）求二面角
的大小（用反三角函数表示）；
（Ⅱ）求点A到平面
的距离.
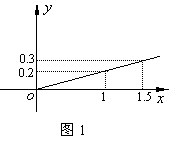
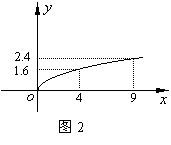
19、（本小题12分）某投资公司计划投资
、
两种金融产品，根据市场调查与预测，产品的利润与投资量成正比例，其关系如图1，产品的利润与投资量的算术平方根成正比例，其关系如图2，（注：利润与投资量单位：万元）
（Ⅰ）分别将、两产品的利润表示为投资量的函数关系式；
（Ⅱ）该公司已有10万元资金，并全部投入、两种产品中，问：怎样分配这10万元投资，才能使公司获得最大利润？其最大利润为多少万元？
 |  | ||
20、（本小题12分）已知函数
的图象过原点，
与
的图象交于不同的两点A，B
（1）若
在
处取得极大值2，求函数
的单调区间；
（2）若使
的值
满足
，求线段AB在轴上的射影长的取值范围
21、（本小题12分）已知曲线C：xy=1，过C上一点
作一斜率为
的直线交曲线C于另一点
，点列
的横坐标构成数列{
}，其中
。（1）求与
的关系式；（2）求证：{
}是一等比数列；（3）求证：
。
22、（本小题14分）过椭圆C：
外一点A（m，0）作一直线l交椭圆于P、Q两点，又Q关于x轴对称点为
，连结
交x轴于点B。
（1）若
，求证：
；（2）求证：点B为一定点
。
江苏省泰兴中学2004-2005学年度第二学期期中考试
高三数学参考答案
一、选择题
1、A 2、B 3、B 4、C 5、A 6、B
7、D 8、C 9、C 10、D 11、B 12、A
二、填空题
13、40 14、2 15、
16、
三、解答题
17、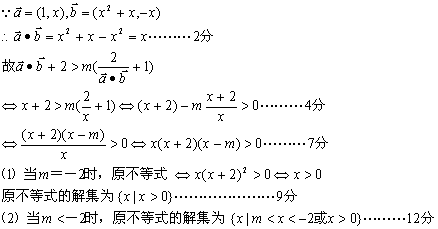
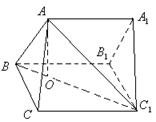18、解：（Ⅰ）
平面，
，
平面 
………………………………2分
所以
为二面角的平面角……………4分
在直角三角形
中，
在直角三角形
中，
所以
………………………………………………………5分
所以二面角的平面角的大小为
………………………6分
（Ⅱ）由于
，
所以
，又平面
则
…………………………………………………8分
从而
平面，所以
为点A到平面的距离………10分
在直角三角形中，
即A到平面的距离为
………12分
19、解：（Ⅰ）设投资为万元，产品的利润为
万元，产品的利润为万元．
由题意设
，
．由图知
，
． ………2分
又
，
．
………………………………4分
从而
，
．………………………………5分
（Ⅱ）设产品投入万元，则产品投入
万元，设企业利润为
万元．
，
令
，则
．
当
时，
，此时
．……………………………11分
答：当产品投入6万元，则产品投入4万元时，该企业获得最大利润，利润为2.8万元．
………………………………………………………12分
20、 由图象过原点，得
由
（1）由在处取得极大值2，得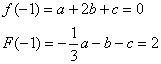
得
（2）
由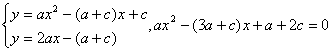
设
，则线段AB在轴上的射影长以及
由
得
，得
21．解：（1）过C：
上一点作斜率为
的直线交C于另一点
，
则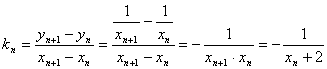
，
于是有：
。 ……（4分）
（2）记
，则
，
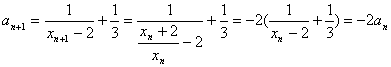因为
，
因此数列{}是等比数列。 ……（8分）
（3）由（2）可知：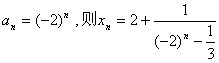
，
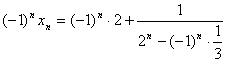。 当n为偶数时有：
=
，
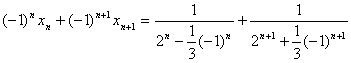
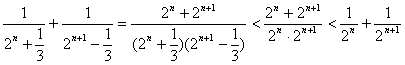于是①在n为偶数时有：
。
②在n为奇数时，前n-1项为偶数项，于是有：
。
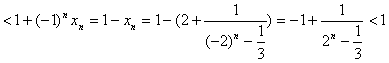综合①②可知原不等式得证。 ……（12分）
22．证明：（1）连结
，因为Q与
关于x轴对称，而A在x轴上，
则在
中，AB平分
，
由内角平分线定理可知：
，
而，∵
同向，故
且
，
则
，又P、B、在同一直线且
与
同向，
于是有：=
。 ……（6分）
（2）设过A（m，0）的直线l与椭圆C：
与Q关于x轴对称，则
， 由
及
相减得
，∴
，
PQ直线方程：
，而PQ过A（m，0），则有：
，
而
，同理可求得：
。
下面利用分析法证明：
。
即证：
……①
只需证：
只需证：
，
即证：
……②
而（
，
）在椭圆上，则
……③
同理 
……④
由③×④可知②成立，从而①式得证。因此成立。∴
。
∴点B为一定点（
，0）。
……（14分）
另法：证（1）设直线l过A（m，0）与椭圆交于
，而与Q关于x轴对称，则，由，则
，
∴
∴=。 ……（6分）
（2）由，则
……①
由=，则
……②
由①×②得 
……③
又 ……④
……⑤
∵
，由④-⑤·
得 
，
，
……⑥
由③⑥可知 。 ∴。
∴点B为一定点（，0）。
……（14分）