江苏省泰兴中学2005届第二次模拟考试
数学
本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．共150分，考试时间120分钟．
第I卷 (选择题，共60分)
注意事项：
1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
2．选出答案后，用铅笔把答题卡上对应的题目的答案标号涂黑，如需改动，用橡皮擦干净后，再填涂其它答案，不能答在试卷上。
一、选择题（本题共12个小题，每小题5分，共60分。在每小题给出的四个选项中，有且只有一个是正确的）
1、下列函数中周期为2的是 （ ）
A．
B．
C．
D．
2、若
的展开式中含有常数项（非零），则正整数n的可能值是（ ）
A．6 B．5 C．4 D．3
3、若命题
，则┐p： （ ）
A．
B．
C．
D．
4、等比数列
则数列
的通项公式为（ ）
A．
B．
C．
D．
5、已知直线m，n，平面
，给出下列命题：
①若
；②若
；③若
；
④若异面直线m，n互相垂直，则存在过m的平面与n垂直.
其中正确的命题是 （ ）
A．②③ B．①③ C．②④ D．③④
6、设F1、F2为椭
的左、右焦点，过椭圆中心任作一直线与椭圆交于P、Q两点、当四边形PF1QF2面积最大时，
的值等于 （ ）
A．0 B．1 C．2 D．4
7、若不等式
成立的充分非必要条件是
，则实数a的取值范围是（ ）
A．
B．
C．
D．
8、底面边长为
，各侧面均为直角三角形的正三棱锥P—ABC的四个顶点都在同一球面上，则此球的表面积为 （ ）
A．
B．
C．
D．
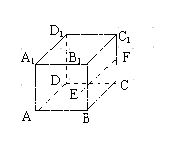
9、在正方体
中，E为正方形ABCD的中心，F为CC1的中点，则EF与AB所成角的正切值为
A．
B．
C．
D．
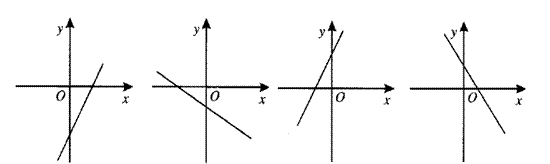10、若函数
的图象的顶点在第四象限，则其导函数
的图象可能是（ ）
A． B． C． D．
11、某校为了了解一次数学质量检测的情况，随机的抽取了100名学生的成绩，并按下表的分数段计数，
| 分数段 | （0, 80 ) | [80, 110) | [110, 150] |
| 频数 | 35 | 50 | 15 |
| 平均成绩 | 60 | 98 | 130 |
则本次检测中所抽样本的平均成绩为（ ）
A．90 B．82 C．96 D．89.5
12、已知直线
不全为0）与圆
有公共点，且公共点的横、纵坐标均为整数，那么这样的直线共有 （ ）
A．66条 B．72条 C．74条 D．78条
第Ⅱ卷 (非选择题，共90分)
注意事项：
1．第Ⅱ共6页，用蓝、黑色的钢笔或圆珠笔直接答在试卷中。
2．答卷前，请将密封线内的项目填写清楚。
| 题号 | 二 | 三 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | |||
| 分数 | ||||||||
二、填空题：（本大题共6小题，每小题4分，共24分）
13、已知双曲线
的一条准线与抛物线
的准线重合，则m的值为
.
14、在锐角三角形ABC中，已知
的面积为
，则
，
的值为
.
15、双曲线
右支上的点P到左焦点的距离为9，则点P的坐标为____________
16、从装有
个球（其中n个白球，1个黑球）的口袋中取出m个球（
，共有
种取法. 在这种取法中，可以分成两类：一类是取出的m个球全部为白球，共有
种取法；另一类是取出的m个球有
个白球和1个黑球，共有
种取法. 显然
成立. 试根据上述思想化简下列式子：
=
三、解答题
17、设F是椭圆
的右焦点，且椭圆上至少有21个不同的点
），使FP1、FP2、FP3、…组成公差为d的等差数列，求公差d的取值范围.
18、A有一只放有x个红球，y个白球，z个黄球的箱子（x、y、z≥0，且
），B有一只放有3个红球，2个白球，1个黄球的箱子，两人各自从自己的箱子中任取一球比颜色，规定同色时为A胜，异色时为B胜.
（1）用x、y、z表示B胜的概率；
（2）当A如何调整箱子中球时，才能使自己获胜的概率最大？
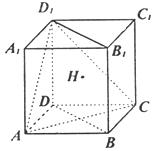19、在棱长为a的正方体ABCD—A1B1C1D1 中，
（1）求证：平面BB1D1D⊥平面ACD1；
（2）求AA1与平面ACD1所成的角；
（3）设H为截面ACD1内一点，求H到正方体表面ADD1A1、
DCC1D1、ABCD的距离之和的最小值.
20、已知函数
.
⑴若函数
在
上单调递减，在
上单调递增，求实数
的值；
⑵是否存在正整数，使得在
上必为单调函数？若存在，试求出 的值，若不存在，请说明理由.
21、已知A（－2，0）、B（2，0），点C、点D满足
（1）求点D的轨迹方程；
（2）过点A作直线l交以A、B为焦点的椭圆于M、N两点，线段MN的中点到y轴的距离为
，且直线l与点D的轨迹相切，求该椭圆的方程.
22、集合A是由适合以下性质的函数
构成的：对于任意的
，
都有
（1）分别判断函数
是否在集合A中？并说明理由；
（2）设函数
，求证：当
江苏省泰兴中学2005届第二次模拟考试
数学参考答案
一、选择题
1、C 2、B 3、A 4、A 5、D 6、C
7、A 8、A 9、C 10、A 11、D 12、B
二、填空题
13、
14、
，2 15、（4，0） 16、
三、解答题
17、解：数列的最小项
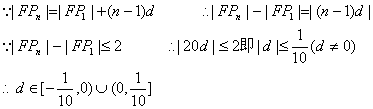
18．解：（1）显然A胜与B胜为对立事件，A胜分为三个基本事件：
①A1：“A、B均取红球”；②A2：“A、B均取白球”；③A3：“A、B均取黄球”.
（2）由（1）知
，
于是
，即A在箱中只放6个红球时，获胜概率最大，其值为
19．解法一：
（1）证：由正方体性质易知
，
又
平面ACD1，所以BB1D1D⊥平面ACD1.
（2）作A1G⊥平面ACD1，垂足为G，连AG，则
为AA1与平面ACD1所成的角.连A1C1，设
，
，∴A1C1//平面ACD1，即A1G等于O1到平面ACD1的距离.
连OO1，OD1在Rt△DO1D1中，作O1E⊥OD1于E，则由（1）知O1E⊥平面ACD1，
又在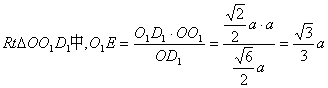
，
所以，
故AA1与平面ACD1所成角为
（利用DD1//AA1，求解同样给分）
（3）由体积法知：距离之和为一定值，为a
若将题目改为求距离的平方和则
分别作HM，HN，HF垂直于平面ADD1A1，DCC1D1，ABCD，则HM2+HN2+HF2=HD2，
，HD最小值为
，故所求距离之和的最小值为
解法二：
以D为原点，射线DA1、DC1、DD1为x、y、z轴的正半轴，建立空间直角坐标系
（1）
由
平面BB1D1D，所以平面BB1D1D⊥平面ACD1.
（2）易知平面ACD1的法向量为
又
，设AA1与平面ACD1所成角为
，
故AA1与平面ACD1所成角为
（3）设H的坐标为
，则
，
又
所求距离之和的最小值为
.
20、答：（1）=2，（2）
21、本小题满分14分
解：（I）设C、D点的坐标分别为C（
，D
，则
），
则
，故
………2分
又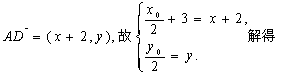
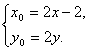…………4分
代入
得
，即为所求点D的轨迹方程.…………7分
（II）易知直线
与
轴不垂直，设直线的方程为
①.
又设椭圆方程为
②.
因为直线与圆相切.故
，解得
将①代入②整理得，
，
而
，即
，
设M（
，N（
，则
，
由题意有
，求得
.经检验，此时
故所求的椭圆方程为
……………14分
22、本小题满分13分
解：（I）
……………1分
证明：任取
，且
，则
因为
所以，
，
所以，
，亦即：
； ……………3分
对于
，只需取
则
而
，所以，
……………6分
（II）因为
属于集合A，所以，任取，则
也即：
① ……………7分
设
，则上式化为：
②
因为
所以
①式对任意的
恒成立，即②式对
恒成立，
可以证明
所以，
