江苏省西亭高级中学高三数学期末测试卷
姓名 班级 得分
一．选择题：(每题5分，共60分)
1.
方程组
的解集是 ( )
(A){(3,4)} (B){(4,3)} (C){(3,4),(4,3)} (D){(x,y)x=3或4，y=4或3}
2.
与代数式
等价的表达式是 ( )
(A)(ln33x+23(4+y)¸sin(a+b)+1 (B) (ln(33x)+23(4+y)¸sin(a+b)+1
(C)(ln33x)+23(4+y))¸(sin(a+b)+1) (D) (ln(33x)+23(4+y))¸(sin(a+b)+1)
3.
设
，则下列不等式①a>b; ②a<b;
③a2>b2;④a2<b2中一定成立的是( )
(A) ①③ (B) ②④ (C) ①④ (D) ②③
4.
复数
的值等于 ( )
(A)i (B)－i (C)1 (D)－1
5. 与330°终边相同的角是 ( )
(A)－60° (B)390° (C)－390° (D)930°
6. 已知P(－4，y)为角a终边上的一点，OP=5，且tana<0，则csca的值是( )
(A)
(B)
(C)
(D)
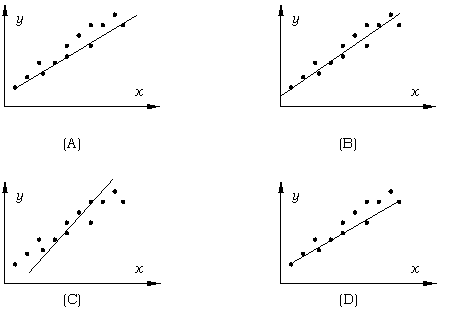
7. 下列四张散点图中，点集的回归直线画得大致正确的是： ( )
 |
8. 已知函数f(x)的定义域为R，则“f(x)为奇函数”是“f(0)=0”的 ( )
(A)充分不必要条件 (B)必要不充分条件(C)充分必要条件 (D)既不充分也不必要每件
9. 下列是关于反函数的一些叙述正确的是 ( )
(A) 单调函数一定有反函数．
(B) 只有单调函数才有反函数．
(C) 周期函数的反函数也是周期函数．
(D) y=sinx,xÎ[0,2p]的反函数是y=arcsinx,xÎ[－1,1]．
10. 圆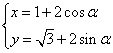
（a为参数）的圆心坐标和半径分别为 ( )
(A)(1,
),2 (B)(－1,－),4 (C)(1,),4
(D)(－1,－),2
11. 抛物线y2=－4x上一点到焦点的距离为4，则它的横坐标是 ( )
(A)－4 (B)－3 (C)－2 (D)－1
12. f(x)以4为周期，且当－2≤x<2时，f(x)=1+x,则f(11.2)的值为 ( )
(A)－3.8 (B)0.2 (C)2.2 (D)12.2
二．填空题：(每题4分，共24分)
13. 已知
且
与
的夹角是钝角，则
的取值范围是
14. 化简：
；
15. 已知：2a=5b=10,则
=______；
16. 已知A(0,5)，B(6,3)，AD^OB于点D，则点D的坐标为_______________．
17. 抛物线y2=2px上任意一点与顶点连线的中点轨迹为__________________．
18. 平面内有n个圆两两相交，任何三个圆不过同一点，写出交点个数随着n的变化而变化的函数关系式f(n):_________________________________.
三．解答题：(共66分)
19. (本题满分12分)在△ABC中，已知(a+b+c)(a+b－c)=3ab，且2cosAsinB=sinC，求证：△ABC为等边三角形．
20. 
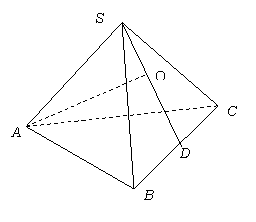(本题满分12分)在正三棱锥S－ABC中，记
a,
b,
c．自底面的顶点A向其所对侧面SBC作垂线，垂足为O，连结并延长SO交BC于D．
(1) (6分)求证：D为BC边的中点；
(2) (2分)设=，用a,b,c表示
；
(3) (4分)三棱锥侧棱长为l，求证：a.b=b.c=c.a=
,并用反三角函数表示∠ASB；
21. (本大题满分10分，第一小题是预备工具推导，所推出的结论在解题(2)时可以直接运用．)
(1)(4分)填空：设向量a=(x,y)，与x轴正方向所成的角为a，则：cosa=________，sina=_________；如果将向量a逆时针旋转90°角到向量b，则向量b与x轴正方向所成角为____________，b的坐标为_______________________(用字母x,y表示)
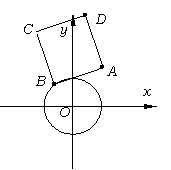
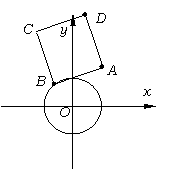
(2)(6分)已知：一个圆
与定点A(3,4)．点B为圆上一个动点，以AB为一边作正方形ABCD(A、B、C、D按顺时针方向排列)，求点D的轨迹；
 |
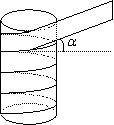
22. (本题满分10分)水管或煤气管经常需要从外部包扎以便对管道起保护作用．包扎时用很长的带子缠绕在管道外部(如图所示)．假定为了节省材料，包扎时要使带子全部包住管道而且带子没有重叠的部分，这就要精确地计算带子的缠绕角度a(如图所示)．
(1) (2分)包扎时带子的缠绕角度a与哪些量有关？
(2) (8分)用字母表示出上述有关的量，并用它们表示出缠绕角a．
 |
23. (本题10分)在50件待检产品中，假设有46件正品，4件次品，那么从中任取5件：
(1) (6分)请写出其中的次品数N的概率分布列；
(2) (2分)至少取到两件次品的概率是多少？
(3) (2分)把一次抽取5件产品的结果视为随机事件，若随机事件出现的概率低于0.05，则视为小概率事件，且认为发生小概率事件是不正常的，那么满足P(N>A)<0.05的最小整数A是多少？这个A你认为有何意义？
24. (本题满分12分)已知：
为定义在R上的奇函数，且当x<－1时，
．
(1) (4分)写出f(x)的函数表达式；
(2) (4分)作出函数的图象并写出f(x)≤6的解集；
(3) (4分)如果f(x+m)≤6的解集为闭区间[0,a]，求m和a的值．
参考解答
一．选择题：C D C A C D B A A A B B
二．填空题：13．
14．
15．1 16.(2,1) 17.
18.f(n)=n2－1
三．解答题：
19. 解 由已知得：
，即
\
即 ∠C=60° (1)
又QC=180°－(A+B)
\sinC=sin(A+B)=sinA.cosB+cosA.sinB
由已知：sinC=2cosA.sinB
\sinA.cosB－cosA.sinB=0即sin(A－B)=0
QA、B为三角形内角，A－BÎ(－180°，180°)
\A－B=0° 即A=B (2)
\由(1)(2)可知：ΔABC为等边三角形
20. 解 (1)Q三棱锥S－ABC为正三棱锥
\SA=SB=SC，∠ASB=∠BSC=∠ASC
\a.b=b.c=a.c
Q
\
即SA^BC 又QAO^平面SBC
\SD^BC(三垂线定理) 又QSB=SC
\D为BC的中点．
(2)
(3)QAO^平面SBC，\AO^SB，即：
\
也即
Q a.b=b.c=a.c 代入上式即得a.b=b.c=c.a=．
又Q a.b=l2.cos∠ASB, \ cos∠ASB=
\∠ASB=arccos．
21. 解 (1)
；
；
；(－y，x)．
(2)设点D(x,y)，则
\
\
也即点B的坐标为(7－y,x+1)
Q点B在圆上
\
也即
此即点D的轨迹方程，它表示点D的轨迹是以点(－1,7)为圆心，半径为3的圆．
22. 
解 (1)缠绕角a显然与管子的直径、带子的宽度有关．
(2) 设管子的直径为D，带子的宽度为W．
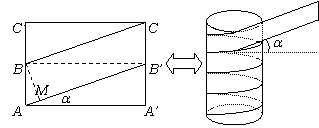
把管子看作圆柱体，设想将侧面沿某一母线剪开后展开，其展开图如图所示．由题意，包扎时要使带子全部包住管道而且带子没有重叠的部分，这就意味着点B与B¢必在同一水平线上．
过点B作BM^AB¢，M为垂足，则BM=W；同时，AA¢=pD，∠A¢AB¢=a．
\在RtΔBMB¢中，sin a=BM:BB¢=W:pD
\
23. 解 (1)抽取的5件产品中的奖品数N的分布列为：
N | 0 | 1 | 2 | 3 | 4 |
| p |
»0.647 |
»0.308 |
»0.043 |
»0.002 |
»0.000 |
(2)由上述分布列可知：p(N≥2)=0.045．
(3)p(N>0)=p(N≥1)=0.353>0.05; p(N>1)=p(N≥2)=0.045<0.05;
\满足P(N>A)<0.05的最小整数A是1．
这个A的意义是：如果取到的次品数大于A，则说明发生了小概率事件，是不正常的．说明整个这批产品中的次品数极可能比假设的要多．(注：A也叫“合格判定数”)
24. 解 (1)令x+1=t，则x=t－1．
当x<－1，即t<0时，f(t)=－(t－1)2+2(t－1)+2=－t2+4t－1
\当x<0时，f(x)=－x2+4x－1．
又Qf(x)为奇函数\f(－x)=－f(x)
(xÎR)
\当x>0，即－x<0时，有
f(x)=－f(－x)=－[－(－x)2+4(－x)－1]= x2+4x+1
另外，由于f(x)为奇函数，故f(0)=0
(2)y=f(x)的图象如图所示：
当x>0时，f(x)≤6的解集为(0,1]
当x<0时，f(x)≥－6的解集为[－1,0)
又f(0)=0
\f(x)≤6的解集为[－1,1]
(3)Qf(x+m)≤6\－1≤x+m≤1
\－1－m≤x≤1－m
\－1－m=0且1－m=a
\m=－1,a=2